4 Classes of Objects: Interface Definitions

In this chapter, we take an alternative perspective on defining sets of objects; we can characterize objects not just by their construction, as done with a data definition, but also by the methods they support. We call this characterization an interface definition. As we’ll see, designing to interfaces leads to generic and extensible programs.

4.1 Lights, revisited

Let’s take another look at the Light data definition we developed in Enumerations. We came up with the following data definition:

;; A Light is one of:

;; - (new red%)

;; - (new green%)

;; - (new yellow%)

We started with a next method that computes the successor for each light. Let’s also add a draw method and then build a big-bang animation for a traffic light.

#lang class/0

(require 2htdp/image)

(define LIGHT-RADIUS 20)

(define-class red%

;; next : -> Light

;; Next light after red

(check-expect (send (new red%) next) (new green%))

(define (next)

(new green%))

;; draw : -> Image

;; Draw this red light

(check-expect (send (new red%) draw)

(circle LIGHT-RADIUS "solid" "red"))

(define (draw)

(circle LIGHT-RADIUS "solid" "red")))

(define-class green%

;; next : -> Light

;; Next light after green

(check-expect (send (new green%) next) (new yellow%))

(define (next)

(new yellow%))

;; draw : -> Image

;; Draw this green light

(check-expect (send (new green%) draw)

(circle LIGHT-RADIUS "solid" "green"))

(define (draw)

(circle LIGHT-RADIUS "solid" "green")))

(define-class yellow%

;; next : -> Light

;; Next light after yellow

(check-expect (send (new yellow%) next) (new red%))

(define (next)

(new red%))

;; draw : -> Image

;; Draw this yellow light

(check-expect (send (new yellow%) draw)

(circle LIGHT-RADIUS "solid" "yellow"))

(define (draw)

(circle LIGHT-RADIUS "solid" "yellow")))

We can now create and view lights:

> (send (new green%) draw)

> (send (new yellow%) draw)

> (send (new red%) draw)

To create an animation we can make the following world:

(define-class world%

(fields light)

(define (tick-rate) 5)

(define (to-draw)

(send (send this light) draw))

(define (on-tick)

(new world% (send (send this light) next))))

(require class/universe)

(big-bang (new world% (new red%)))

At this point, let’s take a step back and ask the question: what is essential to being a light? Our data definition gives us one perspective, which is that for a value to be a light, that value must have been constructed with either (new red%), (new yellow%), or (new green%). But from the world’s perspective, what matters is not how lights are constructed, but rather what can lights compute. All the world does is call methods on the light it contains, namely the next and draw methods. We can rest assured that the light object understands the next and draw messages because, by definition, a light must be one of (new red%), (new yellow%), or (new green%), and each of these classes defines next and draw methods. But it’s possible we could relax the definition of what it means to be a light by just saying what methods an object must implement in order to be considered a light. We can thus take a constructor-agnostic view of objects by defining a set of objects in terms of the methods they understand. We call a set of method signatures (i.e., name, contract, and purpose statement) an interface.

4.2 A light of a different color

So let’s consider an alternative characterization of lights not in terms of what they are, but rather what they do. Well a light does two things: it can render as an image and it can transition to the next light; hence our interface definition for a light is:

;; An ILight implements

;; next : -> ILight

;; Next light after this light.

;; draw : -> Image

;; Draw this light.

Now it’s clear that every Light is an ILight because every Light implements the methods in the ILight interface, but we can imagine new kinds of implementations of the ILight interface that are not Lights. For example, here’s a class that implements the ILight interface:

;; A ModLight is a (new mod-light% Natural)

;; Interp: 0 = green, 1 = yellow, otherwise red.

(define-class mod-light%

(fields n)

;; next : -> ILight

;; Next light after this light.

(define (next)

(new mod-light% (modulo (add1 (send this n)) 3)))

;; draw : -> Image

;; Draw this light.

(define (draw)

(cond [(= (send this n) 0)

(circle LIGHT-RADIUS "solid" "green")]

[(= (send this n) 1)

(circle LIGHT-RADIUS "solid" "yellow")]

[else

(circle LIGHT-RADIUS "solid" "red")])))

Now clearly a ModLight is never a Light, but every ModLight is an ILight. Moreover, any program that is written for ILights will work no matter what implementation we use. So notice that the world program only assumes that its light field is an ILight; this is easy to inspect—the world never assumes the light is constructed in a particular way, it just calls next and draw. Which means that if we were to start our program off with

(big-bang (new world% (new mod-light% 2)))

it would work exactly as before.

4.3 Representation inpedendence and extensibility

We’ve now developed a new concept, that of an interface, which is a collection of method signatures. We say that an object is an instance of an interface whenever it implements the methods of the interface.

The idea of an interface is already hinted at in the concept of a union of objects since a function over a union of data is naturally written as a method in each class variant of the union. In other words, to be an element of the union, an object must implement all the methods defined for the union—the object must implement the union’s interface. But interfaces are about more than just unions. By focusing on interfaces, we can see there are two important engineering principles that can be distilled even from this small program:

1. Representation independence

   As we’ve seen with the simple world program that contains a light, when a program is written to use only the methods specified in an interface, then the program is representation independent with respect to the interface; we can swap out any implementation of the interface without changing the behavior of the program.

2. Extensibility

   When we write interface-oriented programs, it’s easy to see that they are extensible since we can always design new implementations of an interface. Compare this to the construction-oriented view of programs, which defines a set of values once and for all.

These points become increasingly important as we design larger and larger programs. Real programs consist of multiple interacting components, often written by different people. Representation independence allows us to exchange and refine components with some confidence that the whole system will still work after the change. Extensibility allows us to add functionality to existing programs without having to change the code that’s already been written; that’s good since in a larger project, it may not even be possible to edit a component written by somebody else.

Let’s look at the extensiblity point in more detail. Imagine we had developed the Light data definition and its functionality along the lines of HtDP. We would have (we omit draw for now):

;; A Light is one of:

;; - 'Red

;; - 'Green

;; - 'Yellow

;; next : Light -> Light

;; Next light after the given light

(check-expect (next 'Green) 'Yellow)

(check-expect (next 'Red) 'Green)

(check-expect (next 'Yellow) 'Red)

(define (next l)

(cond [(symbol=? 'Red l) 'Green]

[(symbol=? 'Green l) 'Yellow]

[(symbol=? 'Yellow l) 'Red]))

Now imagine if we wanted to add a new kind of light—perhaps to represent a blinking yellow light. For such lights, let’s assume the next light is just a blinking yellow light:

(check-expect (next 'BlinkingYellow) 'BlinkingYellow)

That’s no big deal to implement if we’re allowed to revise next—we just add another clause to next handle 'BlinkingYellow lights. But what if we can’t? What if next were part of a module provided as a library? Well then life is more complicated; we’d have to write a new function, say fancy-next, that handled blinking lights and used next for all non-blinking lights. And while that gets us a new function with the desired behavior, that won’t do anything for all the places the next function is used. If we’re able to edit the code that uses next, then we can replace each use of next with fancy-next, but what if we can’t...? Well then we’re just stuck. If we cannot change the definition of next or all the places it is used, then it is not possible to extend the behavior of next.

Now let’s compare this situation to one in which the original program was developed with objects and interfaces. In this situation we have an interface for lights and several classes, namely red%, yellow%, and green% that implement the next method. Now what’s involved if we want to add a variant of lights that represents a blinking yellow light? We just need to write a class that implements next:

;; Interp: blinking yellow light

(define-class blinking-yellow%

;; next : -> ILight

;; Next light after this blinking yellow light.

(check-expect (send (new blinking-yellow%) next)

(new blinking-yellow%))

(define (next) this))

Notice how we didn’t need to edit red%, yellow%, or green% at all! So if those things are set in stone, that’s no problem. Likewise, programs that were written to use the light interface will now work even for blinking lights. We don’t need to edit any uses of the next method in order to make it work for blinking lights. This program is truly extensible.

4.4 Case Study: Mobiles

Let’s put our newfound interface skills to work by defining an interface and classes to represent mobiles, delicately balanced sculptures of shapes connected by branches.

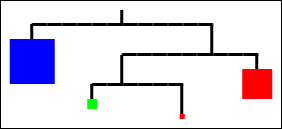
To define mobiles, then, we’ll first need to define simple shapes with weights:

;; An IShape implements:

;;  to-draw: -> Image                 -- renders the IShape

;;  area: -> NonNeg                   -- computes the IShape's area

;;  scale: NonNeg -> IShape           -- returns a new IShape expanded

;;                                       by the given factor

;; A circle% implements IShape and is

;;  (new circle% NonNeg String NonNeg)

;;            -- radius, color, and weight

;; A rect% implements IShape and is

;;  (new rect% NonNeg NonNeg String NonNeg)

;;            -- width, height, color and weight

From these definitions we can easily write the template for our classes:

#lang class/0

(require 2htdp/image)

(define-class circle%

(fields radius color weight)

(define (to-draw) ...)

(define (area) ...)

(define (scale factor) ...))

(define-class rect%

(fields width height color weight)

(define (to-draw) ...)

(define (area) ...)

(define (scale factor) ...))

Now we can move on to define mobiles.

One way to look at the picture above is to see a mobile as a tree structure, with either branch nodes or leaves. The leaves just contain IShapes, while the nodes contain a left mobile, a right mobile, and the lengths of the left and right branches:

;;

;;     +-----------------------------+

;;     | +--------------+            |

;;     v v              |            |

;; A Mobile is one of:  |            |

;;  (new mobile-node% Mobile NonNeg Mobile NonNeg)

;;    -- left mobile, left branch length,

;;       right mobile, right branch length

;;  (new mobile-leaf% IShape)

;;    -- shape hanging at this point

What methods might we want Mobiles to implement? Certainly we want to draw them. Supposing we are modelling a sculpture to hang in a room, we might want to know how much area it takes up, and then scale it larger or smaller to ensure it fits. In other words, we expect Mobiles to implement the IShape interface.

4.5 Sharing Interfaces

;; A Posn implements

;; move-by : Real Real -> Posn

;; move-to : Real Real -> Posn

;; dist-to : Posn -> Real

;; A Segment implements

;; draw-on : Scene -> Scene

;; move-by : Real Real -> Segment

;; move-to : Real Real -> Segment

;; dist-to : Posn -> Real

Notice that any object that is a Segment is also a Posn.