Computer Graphics (CS 4300) 2010S: Example Exam 2 Problems
Exam 2 covers lectures 15 through 22.
- Transform a given 3D point by a given
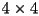 homogeneous transformation matrix.
homogeneous transformation matrix. - Give a sufficient set of conditions that must hold for a
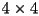 homogeneous transformation matrix to be a pure rotation.
homogeneous transformation matrix to be a pure rotation. - If a
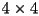 homogeneous transformation matrix is known to be a pure translation, what must be true of its upper-left
homogeneous transformation matrix is known to be a pure translation, what must be true of its upper-left  sub-matrix?
sub-matrix? - Give one advantage and one disadvantage of the Euler angle representation for 3D rotations.
- Let
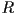 be a
be a 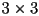 3D rotation matrix. Show how to compute
3D rotation matrix. Show how to compute 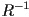 .
. - Let
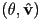 be a 3D rotation in axis-angle form. Give two representations of the inverse rotation.
be a 3D rotation in axis-angle form. Give two representations of the inverse rotation. - What is the purpose of Rodrigues’ rotation formula?
- Let
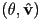 be a 3D rotation in axis-angle form. Show how to construct an equivalent unit quaternion.
be a 3D rotation in axis-angle form. Show how to construct an equivalent unit quaternion. - Show how to rotate a 3D point
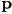 by a unit quaternion
by a unit quaternion 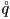 . Then prove that composition of two rotations represented as unit quaternions
. Then prove that composition of two rotations represented as unit quaternions 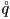 and
and 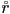 is equivalent to quaternion multiplication. In your setup, which rotation is applied first,
is equivalent to quaternion multiplication. In your setup, which rotation is applied first, 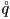 or
or 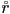 ?
? - Give one advantage and one disadvantage of the unit quaternion representation for 3D rotations.
- Assume you have available a routine that computes quaternion multiplication. Explain how you can use this routine to (a) compute the dot product and (b) compute the cross product of two 3D vectors.
- Let
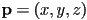 . Consider the set
. Consider the set 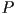 of all values of
of all values of 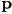 that satisfy the algebraic equation
that satisfy the algebraic equation 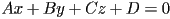 for real nonzero constants
for real nonzero constants 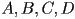 . What kind of geometric object is
. What kind of geometric object is 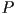 ?
? - Let
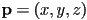 and
and 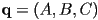 . Rewrite the equation
. Rewrite the equation 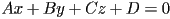 in vector form, using
in vector form, using 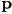 and
and 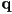 . Explain the geometric significance of
. Explain the geometric significance of 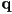 .
. - Give an algebraic equation that must hold for all and only the points
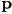 that lie on a sphere with center
that lie on a sphere with center 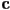 and radius
and radius 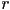 .
. - Let
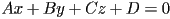 be the implicit form of a plane in 3D, with
be the implicit form of a plane in 3D, with 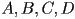 real nonzero constants. What is the unit normal to a given point
real nonzero constants. What is the unit normal to a given point 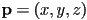 on the surface?
on the surface? - Let
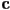 be the center and
be the center and 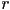 be the radius of a sphere. What is the unit normal to a given point
be the radius of a sphere. What is the unit normal to a given point 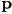 on the sphere?
on the sphere? - Give one mathematical way to define a line in 3D.
- Let
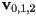 be 3D points that are the vertices of a triangle. Let
be 3D points that are the vertices of a triangle. Let 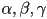 be the barycentric coordinates of a point
be the barycentric coordinates of a point 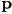 in the plane of the triangle. Show how to compute the Cartesian coordinates of
in the plane of the triangle. Show how to compute the Cartesian coordinates of 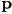 in terms of
in terms of 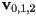 and
and 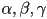 . (Assume that at
. (Assume that at 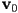
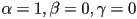 ; at
; at 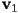
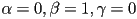 ; and at
; and at 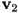
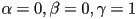 .)
.) - Let
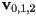 be 3D points that are the vertices of a triangle. Show how to compute a unit normal
be 3D points that are the vertices of a triangle. Show how to compute a unit normal 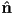 to the triangle such that the vertices appear in CCW order exactly when
to the triangle such that the vertices appear in CCW order exactly when 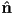 points towards you.
points towards you. - Give two fundamentally different ways that a ray and a sphere in 3D can intersect in a single point. Draw diagrams for each.
- We studied a method to find the intersection of a ray and a sphere that involved solving a quadratic equation. What is the geometric significance of the discriminant of this equation being zero? Less than zero?
- Give the parametric equation for a point
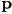 along a ray starting at
along a ray starting at 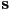 with direction
with direction 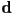 . Let
. Let 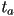 and
and 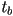 be two solutions to this equation corresponding to the intersections of the ray with a sphere. Which is closer to
be two solutions to this equation corresponding to the intersections of the ray with a sphere. Which is closer to 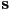 ? Let
? Let 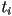 correspond to the intersection closer to
correspond to the intersection closer to 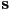 . Give expressions for (a) the radius of the sphere and (b) the surface normal of the sphere at that intersection point in terms of
. Give expressions for (a) the radius of the sphere and (b) the surface normal of the sphere at that intersection point in terms of 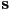 ,
, 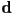 ,
, 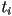 , and the center
, and the center 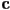 of the sphere.
of the sphere.
- Give two uses in graphics for an algorithm that computes ray/triangle intersections.
- Draw a simple scene graph showing the relationship between a world frame
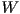 , an object frame
, an object frame 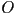 , and a camera frame
, and a camera frame 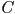 . Let
. Let 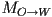 be a homogeneous transform from object frame to world frame, and similarly let
be a homogeneous transform from object frame to world frame, and similarly let 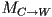 be a homogeneous transform from camera to world frame. Show how to compose these two to produce
be a homogeneous transform from camera to world frame. Show how to compose these two to produce 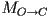 , the homogeneous transform from object to camera frame.
, the homogeneous transform from object to camera frame. - Sketch the appearance of a set of train tracks heading into the distance, viewed obliquely, in (a) parallel and (b) perspective projection.
- Show how to transform a 3D point
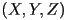 by a projective transformation matrix
by a projective transformation matrix 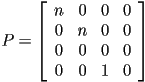 .
.
- Assume you are using the painter’s algorithm to render a set of triangles as viewed from a camera in 3D. This involves sorting the triangles according to their depth in camera frame, but you would like to do this sorting only when required, because it is relatively time consuming. What are two events that would require re-sorting?
- The painter’s algorithm requires sorting
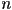 triangles by their depth in camera frame. (a) Give one way to assign a single “depth” value to a triangle with 3D vertices
triangles by their depth in camera frame. (a) Give one way to assign a single “depth” value to a triangle with 3D vertices 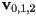 in camera frame (assume that the camera’s viewing direction is
in camera frame (assume that the camera’s viewing direction is 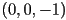 in camera frame). (b) Assuming you do not know any upper bound on
in camera frame). (b) Assuming you do not know any upper bound on 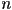 , what is the worst-case running time for an optimal sorting algorithm for the triangles in big-O notation, in terms of
, what is the worst-case running time for an optimal sorting algorithm for the triangles in big-O notation, in terms of 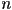 ?
? - Sketch a view of three 3D triangles
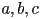 that are an occlusion cycle, i.e., some part of
that are an occlusion cycle, i.e., some part of 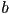 is in front of
is in front of 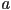 , some part of
, some part of 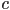 is in front of
is in front of 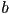 , but some part of
, but some part of 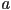 is in front of
is in front of 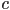 . This is one example of a case where the basic painter’s algorithm fails. Give a second example of another situation, in this case involving only two triangles, where the basic painter’s algorithm also cannot produce a correct rendering.
. This is one example of a case where the basic painter’s algorithm fails. Give a second example of another situation, in this case involving only two triangles, where the basic painter’s algorithm also cannot produce a correct rendering. - Given pseudocode for a basic triangle rasterization algorithm as we have studied, pencil in a set of modifications that would resolve occlusions using the z-buffer method. (Assume that the camera’s viewing direction is
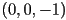 in camera frame.)
in camera frame.)
- Write pseudocode that calculates the “minimum”
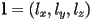 and maximum
and maximum 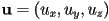 corners of an axis-aligned bounding box for a list of
corners of an axis-aligned bounding box for a list of 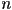 triangles
triangles 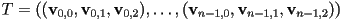 .
. - Given the “minimum”
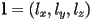 and maximum
and maximum 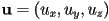 corners of an axis-aligned bounding box
corners of an axis-aligned bounding box 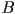 , show one method to compute the center
, show one method to compute the center 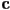 and radius
and radius 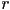 of a bounding sphere that encloses
of a bounding sphere that encloses 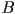 .
. - Let
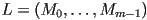 be a list of
be a list of 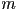 triangle meshes
triangle meshes 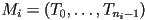 , where every
, where every 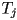 is an individual 3D triangle (mesh
is an individual 3D triangle (mesh 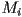 contains
contains 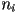 triangles). Let
triangles). Let 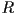 be a 3D ray. Assume you have algorithms
be a 3D ray. Assume you have algorithms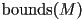 that takes in a triangle mesh and returns a bounding sphere
that takes in a triangle mesh and returns a bounding sphere 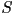 for that mesh
for that mesh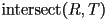 that returns true if
that returns true if 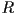 intersects triangle
intersects triangle 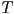 and false otherwise
and false otherwise
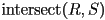 that returns true if
that returns true if 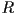 intersects sphere
intersects sphere 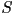 and false otherwise
and false otherwise
Write two pseudocode procedures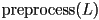 that is called (by other code that you do not have to write) whenever any triangle in any mesh is added, removed, or changes position, and that can create or update a global datastructure to be used to accelerate picking (it is up to you to define this global datastructure)
that is called (by other code that you do not have to write) whenever any triangle in any mesh is added, removed, or changes position, and that can create or update a global datastructure to be used to accelerate picking (it is up to you to define this global datastructure)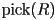 that is called whenever the user has clicked the mouse (by other code that you do not have to write) with
that is called whenever the user has clicked the mouse (by other code that you do not have to write) with 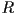 a corresponding pick ray, and that returns one of the meshes
a corresponding pick ray, and that returns one of the meshes 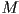 that was intersected by that pick ray, if any, or
that was intersected by that pick ray, if any, or 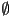 otherwise (if more than one mesh is intersected, you may return any of them).
otherwise (if more than one mesh is intersected, you may return any of them).
For full credit, you must not call 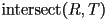 on any triangle
on any triangle 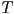 in a mesh
in a mesh 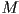 unless
unless 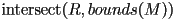 would also return true.
would also return true. - Define frustum culling, backface culling, and occlusion culling.
- Given three 3D points
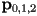 that appear in CCW order from some camera viewpoint, show one method to determine if another 3D point
that appear in CCW order from some camera viewpoint, show one method to determine if another 3D point 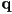 is on the near side or the far side of the plane through
is on the near side or the far side of the plane through 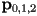 with respect to the camera.
with respect to the camera. - You are given a sketch of a 3D triangle
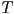 with vertices
with vertices 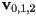 that is cut by a plane such that
that is cut by a plane such that 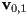 are on one side of the plane and
are on one side of the plane and 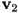 is on the other side, splitting the original triangle into one trapezoid
is on the other side, splitting the original triangle into one trapezoid 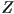 and one smaller triangle
and one smaller triangle 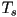 . The intersection of the plane with the triangle is a line segment with endpoints
. The intersection of the plane with the triangle is a line segment with endpoints 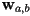 where
where 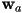 is on the side of the triangle between
is on the side of the triangle between 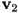 and
and 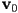 and
and 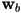 is on the side between
is on the side between 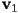 and
and 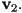 Assume that from some camera
Assume that from some camera 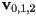 appear in CCW order. (a) What are the vertices of the trapezoid
appear in CCW order. (a) What are the vertices of the trapezoid 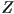 as they would appear to the same camera in CCW order? (b) What are the vertices of the smaller triangle
as they would appear to the same camera in CCW order? (b) What are the vertices of the smaller triangle 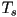 as they would appear to the same camera in CCW order? (c) Split
as they would appear to the same camera in CCW order? (c) Split 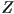 into two triangles by sketching in one of its diagonals, and give the vertices of these triangles in CCW order as they would appear to the same camera.
into two triangles by sketching in one of its diagonals, and give the vertices of these triangles in CCW order as they would appear to the same camera.
- You are given a table with four columns labeled “point”, “directional”, “spot”, and “ambient”, referring to the four types of lights that we have studied, and four rows labeled “position
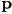 ”, “direction
”, “direction 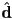 ”, “angle
”, “angle 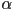 ”, and “intensity
”, and “intensity 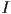 ”. Fill in the table with checkmarks to show which properties are needed to define each type of light.
”. Fill in the table with checkmarks to show which properties are needed to define each type of light. - You are given a sketch of the side-on view of a small patch of a 3D surface at a point
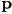 . A point light is also shown at a location
. A point light is also shown at a location 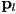 and a camera at location
and a camera at location 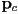 . Sketch in (a) the outward pointing surface normal unit vector
. Sketch in (a) the outward pointing surface normal unit vector 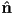 at
at 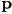 ; (b) the unit vector
; (b) the unit vector 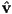 from
from 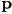 towards the camera; (c) the unit vector
towards the camera; (c) the unit vector  from
from 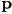 towards the light. (d) Show the math to compute
towards the light. (d) Show the math to compute 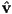 and
and  from the given data. (e) Assume that the ambient and diffuse colors of the surface are given as RGB triples
from the given data. (e) Assume that the ambient and diffuse colors of the surface are given as RGB triples 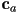 and
and 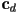 , respectively. Write pseudocode to compute the apparent color
, respectively. Write pseudocode to compute the apparent color 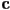 of the surface as it would appear from the camera, according to the Lambertian shading model we have studied, including both ambient and diffuse terms. Use the same scalar intensity
of the surface as it would appear from the camera, according to the Lambertian shading model we have studied, including both ambient and diffuse terms. Use the same scalar intensity 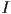 for the light in both terms. This code should assume that
for the light in both terms. This code should assume that 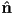 ,
, 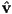 , and
, and  are already available, along with
are already available, along with 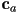 and
and 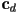 . The code should be correct for all geometric situations, not just the one pictured. In particular, make sure to correctly handle the case that
. The code should be correct for all geometric situations, not just the one pictured. In particular, make sure to correctly handle the case that 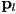 is behind the surface.
is behind the surface. - We studied a shading model that included separate ambient, diffuse, and specular components. Consider a scene with a single sphere illuminated by one ambient light with intensity
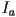 and one directional light with intensity
and one directional light with intensity 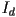 . The ambient light only contributes to the ambient shading term; the directional light contributes to the diffuse and specular shading terms, but not ambient. Several pictures are given of the scene with different settings of the following variables
. The ambient light only contributes to the ambient shading term; the directional light contributes to the diffuse and specular shading terms, but not ambient. Several pictures are given of the scene with different settings of the following variables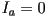 or
or 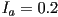
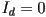 or
or 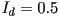
- specular shading enabled or disabled
Mark the value of each of those three variables that must have been in effect to produce each picture. - List at least three real-world light effects that are not typically implemented in a basic rasterization framework, such as OpenGL, that is based on the z-buffer method and the Lambertian and Blinn-Phong shading equations we have studied. [Hint: some such effects are typically implemented in ray tracers; also, with extra work, at least some of these effects can be added to a rasterizer, especially when texture mapping is available.]
- You are given the terms “rasterization” and “ray tracing” in a left column and the terms “object-order rendering” and “image-order rendering” in a right column. Draw two lines, each connecting a term in the left column with the synonymous term in the right column.
- Assume you have
- a list of “surface” objects in world frame
- a function
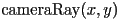 that can create a 3D ray in world frame that starts at the location of a camera and goes through image plane pixel
that can create a 3D ray in world frame that starts at the location of a camera and goes through image plane pixel 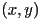
- a function
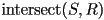 that returns a scalar
that returns a scalar 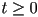 that is either the nearest intersection of a ray
that is either the nearest intersection of a ray 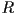 with a surface
with a surface 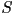 , or
, or 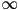 if the ray does not intersect the surface
if the ray does not intersect the surface - a function
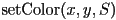 that sets the color of pixel
that sets the color of pixel 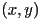 to the ambient color of surface
to the ambient color of surface 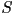 .
.
Write pseudocode for a basic ray tracer that sets each pixel in a 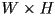 canvas to the ambient color of the nearest surface, or to black if no surface is intersected by a ray from the camera through that pixel.
canvas to the ambient color of the nearest surface, or to black if no surface is intersected by a ray from the camera through that pixel. - Assume you have
- a list of “surface” objects in world frame
- a point light at location
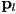 in world frame
in world frame - a function
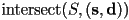 that returns a scalar
that returns a scalar 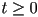 that is either the nearest intersection of a ray with start point
that is either the nearest intersection of a ray with start point 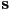 and direction
and direction 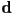 with a surface
with a surface 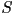 , or
, or 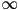 if the ray does not intersect the surface (i.e. if
if the ray does not intersect the surface (i.e. if 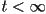 then the intersection point is
then the intersection point is 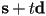 ; note that
; note that 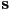 and
and 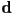 are both given in world frame, and that
are both given in world frame, and that 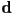 does not necessarily need to be a unit vector)
does not necessarily need to be a unit vector)
Write pseudocode that determines if the point light is in shadow at a given point 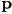 on some surface
on some surface 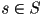 .
. - (a) State the mirror reflection law. [Hint: you may want to use the phrases “angle of incidence” and “angle of reflection”.] (b) You are given a diagram showing a small patch of a 3D surface viewed side-on. The outward pointing surface normal at a point
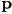 is shown as a unit vector
is shown as a unit vector 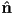 . A unit vector from
. A unit vector from 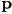 towards a camera is shown as
towards a camera is shown as 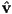 . Give the math to compute
. Give the math to compute 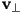 , the component of
, the component of 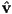 perpendicular to the surface, and
perpendicular to the surface, and 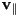 , the component of
, the component of 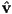 parallel to the surface. These should be set up so that
parallel to the surface. These should be set up so that 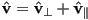 . Sketch in
. Sketch in 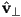 and
and 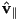 . (c) Give the math to compute
. (c) Give the math to compute 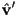 , a unit vector in the direction that a ray from the camera would reflect after bouncing off the surface at
, a unit vector in the direction that a ray from the camera would reflect after bouncing off the surface at 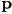 according to the mirror reflection law. You may use
according to the mirror reflection law. You may use 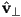 and
and 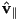 in your calculation of
in your calculation of 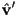 . Finally, sketch in
. Finally, sketch in 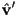 .
. - You are given pictures of two solid objects
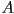 and
and 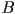 , along with four additional pictures that are the result of applying boolean constructive solid geometry (CSG) operations to
, along with four additional pictures that are the result of applying boolean constructive solid geometry (CSG) operations to 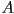 and
and 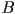 . Label each of the latter four pictures with the corresponding operation that was performed, i.e.
. Label each of the latter four pictures with the corresponding operation that was performed, i.e. 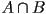 ,
, 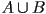 ,
, 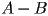 , or
, or 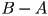 .
. - List at least three real-world lighting effects that are not captured in the standard Lambertian and Blinn-Phong shading equations, and that are not typically implemented (without using texture mapping) in a rasterization framework like OpenGL, but that are not hard to implement in a ray tracer.
- When implementing texture mapping, it is necessary both to handle the case where a large part of a texture image (i.e. many texels) are mapped to a single image pixel (texture minification), as well as the case where a single texel is mapped to multiple image pixels (texture magnification). We have studied the MIP-Mapping technique, which pre-computes a set of scaled-down versions of the original texture image. Does MIP-Mapping help with texture minification, magnification, or both? Explain a scenario where MIP-Mapping could greatly accelerate rendering.
- List at least two real-world lighting effects that are not captured in the standard Lambertian and Blinn-Phong shading equations, and that are not typically implemented in a rasterization framework like OpenGL, but that are often added (at least to some approximation) in practice by careful use of texture mapping. [Hint: some common strategies have two-word names of the form “___ mapping”.]
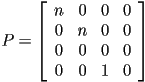 .
.