Computer Graphics (CS 4300) 2010S: Lecture 15
Today
- HW4 out
- homogeneous transforms in 3D
- 3D rotation representations
- assign presentation schedule
- another advantage of the homogeneous transform matrix formalism is that it extends directly to 3D
- in 2D a homogeneous transformation matrix is
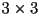 and has the form
and has the form 
- in 3D a homogeneous transformation matrix is
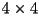 and has the form
and has the form 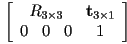
- in either case, to transform a point
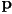 , extend the point with an extra 1 (not zero) and then left multiply by the matrix:
, extend the point with an extra 1 (not zero) and then left multiply by the matrix: 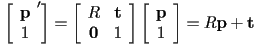
- the submatrix
 includes all rotation, reflection, scaling, and shearing, and the vector
includes all rotation, reflection, scaling, and shearing, and the vector  adds any translation
adds any translation - composition and inversion of transforms follows the same form as for 2D
- standard matrix multiplication and inversion are correct, but we can take advantage of the special form of homogeneous transformation matrices (that the bottom row is always
 ) to come up with more efficient formulas
) to come up with more efficient formulas - if
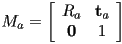 and
and 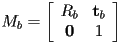 then
then 
- if
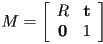 then
then 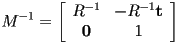
- as for 2D, we can break 3D transformations into two categories: rigid and non-rigid
- the rigid transformations are still translation, rotation, and reflection
- the non-rigid transformations are still scaling and shearing
- translating
- when the upper-left submatrix
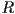 is the identity matrix, the homogeneous transform reduces to a pure translation by
is the identity matrix, the homogeneous transform reduces to a pure translation by 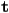 :
: 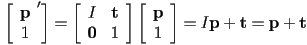
- rotating
- a homogeneous transform
 is a pure rotation when the following conditions hold
is a pure rotation when the following conditions hold
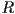 is orthonormal
is orthonormal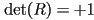
- The first condition is obvious (no translation). The second two conditions mean that the columns of
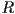 can be visualized as a basis
can be visualized as a basis 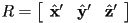 for a rotated coordinate system. The columns are literally unit vectors in the direction of each coordinate axis of the rotated system, expressed as coordinate vectors in the parent frame.
for a rotated coordinate system. The columns are literally unit vectors in the direction of each coordinate axis of the rotated system, expressed as coordinate vectors in the parent frame.
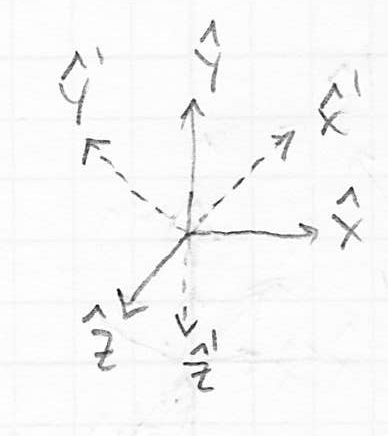
- It may not be intuitive, but the third condition ensures that the rotated coordinate frame is right-handed; the first condition alone would allow either a right or left-handed child frame. If the child frame is left-handed (assuming the parent frame is right-handed) then the transformation would not be a pure rotation, it would also include a reflection.
- for rotation in 2D,
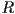 is
is 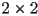 , and we know that it has the form
, and we know that it has the form 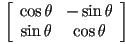 , where
, where  is the CCW rotation from the parent frame
is the CCW rotation from the parent frame 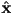 to the rotated frame
to the rotated frame 
- we can begin to extend this to 3D by just using this as the upper left
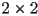 submatrix of a
submatrix of a 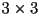 matrix which is otherwise the identity (ones along the major diagonal and zero everywhere else):
matrix which is otherwise the identity (ones along the major diagonal and zero everywhere else): 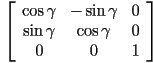
- this has the effect of rotating the child frame by
 CCW radians about the
CCW radians about the 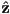 axis of the parent frame, and we can define a function
axis of the parent frame, and we can define a function  as a shorthand for rotation matrices of this form
as a shorthand for rotation matrices of this form
- any 3D rotation can be formed as the composition of three 2D rotations about orthogonal axes
- so far we have a rotation about
 , so we can complete the picture by deriving functions that produce rotation matrices about
, so we can complete the picture by deriving functions that produce rotation matrices about  and
and 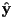
- using the right hand rule, notice that CCW rotation about
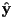 rotates
rotates 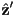 towards
towards 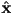
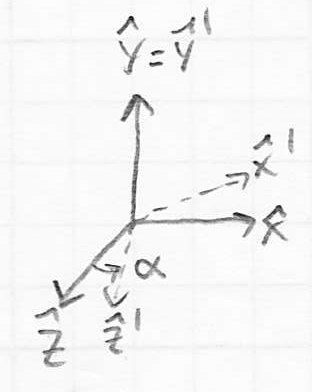
- so
 (notice that the
(notice that the 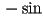 is in the opposite location for
is in the opposite location for 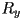 )
) - similarly, CCW rotation about
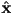 rotates
rotates 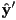 towards
towards 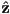
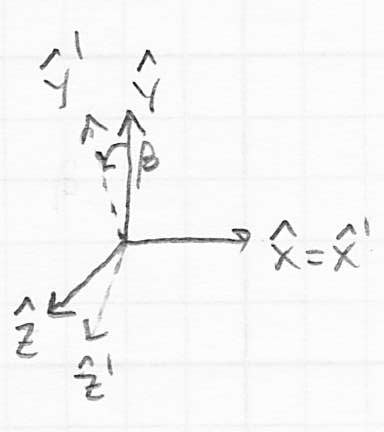
- so

- finally, we can compose these together to produce a general
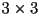 3D rotation matrix:
3D rotation matrix: 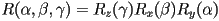
- note that the order of the composition matters
- any order is sufficient, but if someone tells you
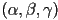 , then you both also need to agree on the order of rotation about the three different axes
, then you both also need to agree on the order of rotation about the three different axes - the
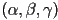 parameters are called Euler angles when using the specific sequence
parameters are called Euler angles when using the specific sequence 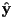 -
-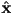 -
-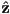 (also called heading (or yaw), pitch, and roll)
(also called heading (or yaw), pitch, and roll) - sometimes this term is used to refer to any three-angle convention
- though it may not be obvious, there are a few issues with representing a 3D rotation with three angles, especially when it comes to interpolating 3D rotations in an animation; we will discuss this more later and introduce some new representations that can be helpful in that case
- reflecting
- in 2D we reflected about either the
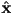 or
or 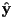 coordinate axis by starting with
coordinate axis by starting with  and then flipping one of the diagonal entries from
and then flipping one of the diagonal entries from 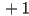 to
to 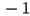
- in 3D we do not reflect about an axis, but rather a coordinate plane
- to reflect about the
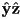 plane, use
plane, use 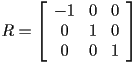
- to reflect about the
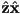 plane, use
plane, use 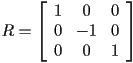
- to reflect about the
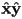 plane, use
plane, use 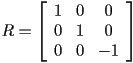
- as in 2D, the composition of two reflections is no longer a reflection: it is a rotation
- the composition of three reflections is still a reflection
- scaling
- in 2D we scaled along the
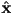 and/or
and/or 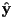 coordinate axis by starting with
coordinate axis by starting with  and then setting each diagonal entry to the desired non-negative scale factor for the corresponding axis
and then setting each diagonal entry to the desired non-negative scale factor for the corresponding axis - we can do the same in 3D:
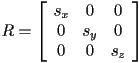 scales each of the three coordinate axes by the indicated amount
scales each of the three coordinate axes by the indicated amount - again, if the scale amounts are different for different axes, then the scale is non-uniform; if they are all the same then the scale is uniform
- shearing
- in 2D we formed a shear matrix by starting with
 , selecting one of the basis vectors
, selecting one of the basis vectors  to remain fixed, and then shifting the other basis vector in the direction of
to remain fixed, and then shifting the other basis vector in the direction of 
- the same approach works in 3D
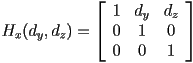 shears the
shears the 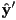 and
and 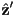 axes in the direction of
axes in the direction of 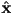
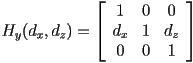 shears the
shears the  and
and 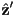 axes in the direction of
axes in the direction of 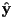
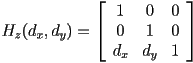 shears the
shears the  and
and 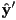 axes in the direction of
axes in the direction of 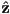
3D Rotation Representations
- the main additional challenge in 3D is handling rotation
- so far we have actually seen two representations for 3D rotations: Euler angles
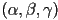 and
and  rotation matrices
rotation matrices - these approaches work well in many situations, specifically
- the rotation matrix representation makes it easy to compose and invert rotations
- it is also easy to rotate a given point using a rotation matrix
- if the orientations of an asymmetric 3D object at two keyframes in an animation are given as Euler angles
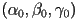 and
and 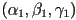 , then it does work to linearly interpolate each angle, e.g.
, then it does work to linearly interpolate each angle, e.g.  (though see below for more discussion of this)
(though see below for more discussion of this)- note that it is not correct to linearly interpolate all 9 entries of the corresponding rotation matrices—this can produce intermediate matrices that are not orthogonal
- Euler angles are a minimal representation because they only require three numbers, and an asymmetric free-floating object in 3D has three rotational degrees of freedom (DoF)
- Euler angles can be converted to a rotation matrix by multiplying
 as above
as above - it is also possible, but more mathematically involved, to convert from a rotation matrix to Euler angles
- nevertheless, at there are some problems with these approaches:
- Euler angles are susceptible to gimbal lock (described below)
- interpolation of Euler angles does not always produce an intuitive looking animation
- gimbal lock
- consider carefully the family of Euler angle 3D rotations with
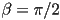
- it turns out that in this case, the effect of
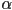 on the pose of the child frame is exactly the same as the effect of
on the pose of the child frame is exactly the same as the effect of 
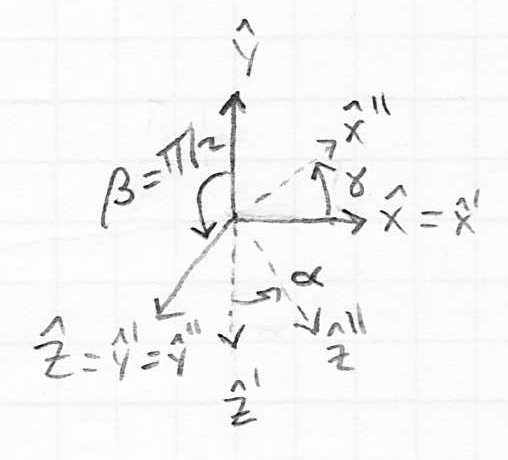
- while in reality any free-floating asymmetric object in 3D always has three rotational degrees of freedom (as well as three translational DoF), the Euler angle representation has a problem (technically, a singularity) when
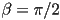 : in that case, the representation degenerates because two of its three parameters become equivalent
: in that case, the representation degenerates because two of its three parameters become equivalent - though it may not be intuitive, this can be a real problem in practice
- fortunately, Euler angles are not the only way to represent 3D rotations
- Euler’s theorem: any 3D rotation is equivalent to a 2D rotation about some axis (line) in space
- this leads to a different rotation representation called axis-angle; more below
- interpolation of rotations
- given two orientations of an asymmetric object, say at two keyframes of an animation, we often need to define an interpolation that defines the orientation of the object at any intermediate time
- if the start and end orientations are given as Euler angles
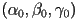 and
and 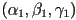 , then it is not incorrect to simply linearly interpolate each angle, e.g.
, then it is not incorrect to simply linearly interpolate each angle, e.g. 
- however, this does not always produce an intuitive animation—the object may appear to get from the first to the second orientation by a “strange” motion
- again, one solution for this issue is to use a different representation for 3D rotation for the purposes of interpolation
- here, quaternions are commonly used
- these are strongly related to the axis-angle representation
- axis-angle representation
- recall that even our Euler angle and rotation matrix representations were restricted to only describing rotations that leave the origin fixed
- this is not a problem—we want the origin to remain fixed for any pure rotation
- we can rotate about any other arbitrary point
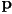 by composing a pure rotation
by composing a pure rotation 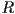 with two translations:
with two translations: 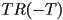 , where the translation transform
, where the translation transform  just has
just has 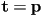
- Euler’s theorem (above) establishes that we can also define any pure rotation by giving a unit vector
 along the axis of rotation (which must go through the origin) and an angle
along the axis of rotation (which must go through the origin) and an angle  of the CCW rotation in radians about
of the CCW rotation in radians about 
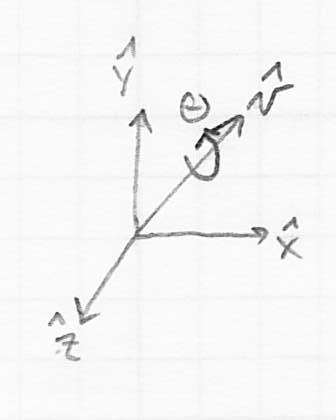
- the pair
 is called an axis-angle representation
is called an axis-angle representation- sometimes the order is reversed, i.e.
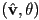
- note that this requires four numbers; Euler angles only required three
- thus the axis-angle representation seems redundant—it has one extra number
- but there is a hidden constraint:

- four parameters minus one constraint again yields three DoF
- another way to think of this is that
 identifies a point on the unit sphere centered at the origin
identifies a point on the unit sphere centered at the origin- this sphere has a two-dimensional surface, so
 has two DoF, not three
has two DoF, not three
- [the third DoF is of course contributed by
 ]
] - advantage: the axis-angle representation does not suffer from gimbal lock, and produces intuitive interpolation of orientations
- if you can find the axis-angle representation
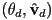 for the differential rotation from one given orientation to another, then linear interpolation from
for the differential rotation from one given orientation to another, then linear interpolation from  to
to 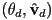 (i.e. linear interpolation of
(i.e. linear interpolation of  from
from  to
to 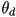 ) works well
) works well - how to find
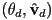 ?
?- one way is to convert whatever representations the first and second orientation are given in into
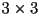 rotation matrices
rotation matrices  and
and 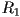
- then the differential rotation is also represented by a
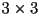 rotation matrix
rotation matrix  where
where  , or
, or 
- then convert
 back to axis angle representation
back to axis angle representation 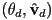
- it is possible to convert among the rotation matrix, Euler angles, and axis-angle representations, so this can all be done, but the math can be somewhat involved
- disadvantage: the axis-angle representation requires conversion to another form (and then conversion back) if we want to compose rotations
- this is precisely why we suggested converting to rotation matrices to compute
 above
above - this motivates a related representation called quaternions, which we will study below
- a few more notes on the axis-angle representation
- the inverse rotation corresponding to
 can either be computed as
can either be computed as 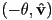 or
or  , i.e. the opposite rotation about the same axis, or the same rotation about the opposing axis
, i.e. the opposite rotation about the same axis, or the same rotation about the opposing axis - since the inverse of an inverse is again the original object, it is easily seen that
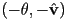 is the same rotation as
is the same rotation as 
- it is possible to compute the rotated image
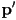 of an arbitrary point
of an arbitrary point 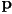 using Rodrigues’ rotation formula:
using Rodrigues’ rotation formula: 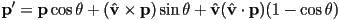 (derivation on Wikipedia)
(derivation on Wikipedia) - but this is usually more computationally expensive than rotating a point with a rotation matrix (
 ), in part because of the need to compute
), in part because of the need to compute 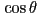 and
and 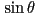
- Unit Quaternions
- like the axis-angle representation, a quaternion
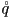 is composed of a 3D vector
is composed of a 3D vector 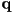 and a scalar
and a scalar 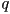 :
: 
- quaternions are commonly used to represent rotations, but they are a more general mathematical concept: they are essentially a higher-dimensional extension of the idea of complex numbers—numbers with a real part and an imaginary part
- the “real” part of a quaternion is the scalar, and the “imaginary” part is the vector
- we will mainly treat them as a rotation representation, but you should be aware of this more general concept
- quaternions can represent a rotation in a similar (but not identical) way to the axis-angle representation
- to properly represent a rotation, we must have a special kind of quaternion called a unit quaternion
- a quaternion
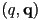 has unit magnitude iff
has unit magnitude iff 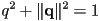
- when this is true, we can consider
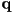 to be a vector along the axis of the rotation, with magnitude
to be a vector along the axis of the rotation, with magnitude 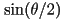 , where
, where  is the amount of rotation about the axis in CCW radians
is the amount of rotation about the axis in CCW radians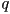 to be
to be 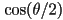
- thus the axis-angle
 is equivalent to the quaternion
is equivalent to the quaternion 
- note, given the trig identity
 , we can easily show that
, we can easily show that 
- just as we had a geometric interpretation for the vector part of an axis-angle representation (it can be thought of as a point on the unit sphere in 3D), there is a geometric interpretation for an entire unit quaternion (not just the vector part): the space of all unit quaternions is the unit sphere in 4D
- this comes from the constraint
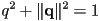
- the quaternion
 can be thought of as a 4D vector
can be thought of as a 4D vector 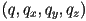 by just appending the scalar part
by just appending the scalar part 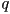 to the three components of the vector part
to the three components of the vector part 
- then requiring
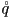 to be a unit quaternion is equivalent to requiring that 4D vector to have unit length:
to be a unit quaternion is equivalent to requiring that 4D vector to have unit length: 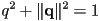 expands out to
expands out to 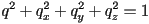
- major benefits of the unit quaternion representation:
- it is relatively efficient to compose and invert rotations represented as unit quaternions
- is is also not too complicated to rotate a given point
- finally, the unit quaternion representation is not subject to gimbal lock, and interpolation of rotations works very well
- composition and point rotation are both implemented in terms of a new multiplication operation defined on quaternions
- we will cover this below, followed by quaternion interpolation; first let’s look at how to take the inverse of a quaternion
- let
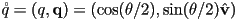 be a unit quaternion corresponding to the axis-angle
be a unit quaternion corresponding to the axis-angle 
- since we know that
 is the inverse rotation in axis-angle form, we can see that
is the inverse rotation in axis-angle form, we can see that  is the inverse rotation in unit quaternion form
is the inverse rotation in unit quaternion form - we also know that
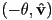 is the inverse rotation in axis-angle form, but this gives exactly the same inverse in unit quaternion form, since
is the inverse rotation in axis-angle form, but this gives exactly the same inverse in unit quaternion form, since  and
and 
- the conjugate unit quaternion
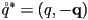 corresponds to the inverse of the rotation corresponding to
corresponds to the inverse of the rotation corresponding to 
- we also know that
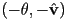 is the same rotation as
is the same rotation as  in axis-angle form
in axis-angle form- this is just re-affirmed by computing
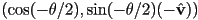
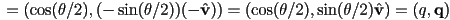
- but observe that
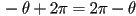 is the same rotation as
is the same rotation as 
- and that
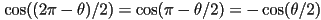 and
and 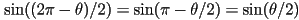 (using trigonometric angle sum identities)
(using trigonometric angle sum identities) - then
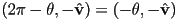 is also the same rotation as
is also the same rotation as 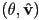 , but now we have the corresponding quaternion
, but now we have the corresponding quaternion 
- thus
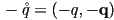 is the same rotation as
is the same rotation as  : antipodal unit quaternions represent the same rotation
: antipodal unit quaternions represent the same rotation
- we now come to quaternion multiplication
- define
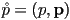 ,
,  , and
, and 
- then the quaternion product
 is calculated as
is calculated as 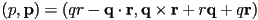
- this may look strange, but it is defined that way for good reasons
- if
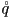 and
and 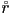 are unit quaternions corresponding to 3D rotations, then
are unit quaternions corresponding to 3D rotations, then  is a unit quaternion corresponding to the composition of those rotations in order (
is a unit quaternion corresponding to the composition of those rotations in order (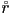 is performed first, then
is performed first, then 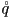 )
) - to rotate a point
 by a rotation represented by the unit quaternion
by a rotation represented by the unit quaternion 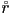 , extend
, extend  to a quaternion (not necessary of unit magnitude) by appending a 0 as the scalar part:
to a quaternion (not necessary of unit magnitude) by appending a 0 as the scalar part: 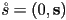 , and then the rotated point
, and then the rotated point 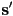 is computed as
is computed as 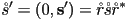
- finally, it can be shown that the conjugate of a composition of quaternions is the composition of the conjugates in the reverse order:

- this confirms that rotating a point by the composition of quaternions
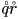 does apply
does apply 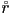 first:
first: 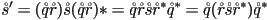
- finally, to interpolate from an orientation represented as unit quaternion
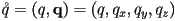 to any other orientation represented as unit quaternion
to any other orientation represented as unit quaternion 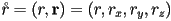 , use a procedure called spherical linear interpolation (SLERP)
, use a procedure called spherical linear interpolation (SLERP)- idea: think of
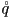 and
and 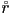 as points on the unit sphere in 4D; SLERP will interpolate an intermediate point on the sphere along the arc of the great circle between them
as points on the unit sphere in 4D; SLERP will interpolate an intermediate point on the sphere along the arc of the great circle between them - first compute
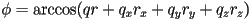
- now we can find the interpolated rotation
 corresponding to any value of a scalar parameter
corresponding to any value of a scalar parameter 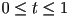
- if
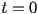 or
or  return
return 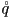
- if
 or
or  return
return 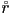
- otherwise return
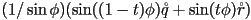
Next Time
 ) to come up with more efficient formulas
) to come up with more efficient formulas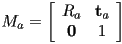 and
and 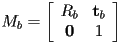 then
then 
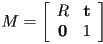 then
then 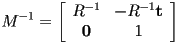
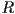 is the identity matrix, the homogeneous transform reduces to a pure translation by
is the identity matrix, the homogeneous transform reduces to a pure translation by 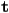 :
: 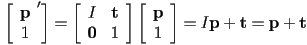
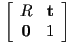 is a pure rotation when the following conditions hold
is a pure rotation when the following conditions hold
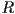 is orthonormal
is orthonormal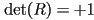
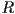 can be visualized as a basis
can be visualized as a basis 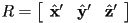 for a rotated coordinate system. The columns are literally unit vectors in the direction of each coordinate axis of the rotated system, expressed as coordinate vectors in the parent frame.
for a rotated coordinate system. The columns are literally unit vectors in the direction of each coordinate axis of the rotated system, expressed as coordinate vectors in the parent frame. 
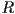 is
is 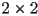 , and we know that it has the form
, and we know that it has the form 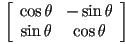 , where
, where  is the CCW rotation from the parent frame
is the CCW rotation from the parent frame 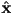 to the rotated frame
to the rotated frame 
 submatrix of a
submatrix of a  matrix which is otherwise the identity (ones along the major diagonal and zero everywhere else):
matrix which is otherwise the identity (ones along the major diagonal and zero everywhere else): 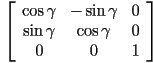
 CCW radians about the
CCW radians about the 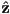 axis of the parent frame, and we can define a function
axis of the parent frame, and we can define a function  as a shorthand for rotation matrices of this form
as a shorthand for rotation matrices of this form 
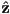 , so we can complete the picture by deriving functions that produce rotation matrices about
, so we can complete the picture by deriving functions that produce rotation matrices about 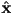 and
and 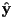
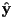 rotates
rotates 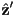 towards
towards 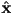

 (notice that the
(notice that the 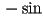 is in the opposite location for
is in the opposite location for 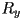 )
)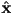 rotates
rotates 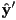 towards
towards 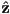


 3D rotation matrix:
3D rotation matrix: 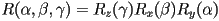
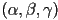 , then you both also need to agree on the order of rotation about the three different axes
, then you both also need to agree on the order of rotation about the three different axes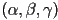 parameters are called Euler angles when using the specific sequence
parameters are called Euler angles when using the specific sequence 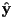 -
-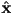 -
-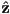 (also called heading (or yaw), pitch, and roll)
(also called heading (or yaw), pitch, and roll)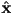 or
or 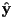 coordinate axis by starting with
coordinate axis by starting with  and then flipping one of the diagonal entries from
and then flipping one of the diagonal entries from 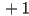 to
to 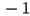
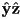 plane, use
plane, use 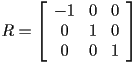
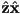 plane, use
plane, use 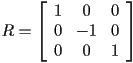
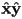 plane, use
plane, use 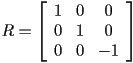
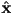 and/or
and/or  coordinate axis by starting with
coordinate axis by starting with  and then setting each diagonal entry to the desired non-negative scale factor for the corresponding axis
and then setting each diagonal entry to the desired non-negative scale factor for the corresponding axis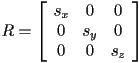 scales each of the three coordinate axes by the indicated amount
scales each of the three coordinate axes by the indicated amount , selecting one of the basis vectors
, selecting one of the basis vectors  to remain fixed, and then shifting the other basis vector in the direction of
to remain fixed, and then shifting the other basis vector in the direction of 
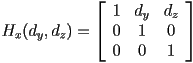 shears the
shears the  and
and  axes in the direction of
axes in the direction of 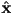
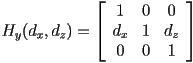 shears the
shears the  and
and  axes in the direction of
axes in the direction of 
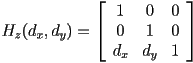 shears the
shears the  and
and  axes in the direction of
axes in the direction of