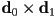Computer Graphics (CS 4300) 2010S: Lecture 16
Today
- surfaces in 3D
- triangles and barycentric interpolation in 3D
- curves in 3D
- 3D ray intersection with sphere, plane, and triangle
Surfaces in 3D
- in 3D, surfaces play the role that curves played in 2D
- yes, you read that right
- a curve (whether in 2D or 3D) is a one-dimensional object
- surfaces are two-dimensional objects and only exist in 3D (well, we could say that the entire 2D plane is a “surface”)
- thus curves are objects with dimension one less than the enclosing space in 2D, and surfaces are objects with dimension one less than the enclosing space in 3D
- an unconstrained point
 in 2D has two Degrees of Freedom (DoF), similarly, an unconstrained point in 3D
in 2D has two Degrees of Freedom (DoF), similarly, an unconstrained point in 3D 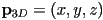 has three DoF
has three DoF - recall that specifying a constraint (an algebraic equation that must hold on variables that are the coordinates of the point, i.e. on
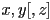 ) removes one DoF
) removes one DoF - it is for this reason that an implicit curve in 2D is specified as an algebraic equation, but in 3D such an equation yields an implicit surface, not a curve
- example:
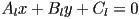 is the implicit equation for a line in 2D
is the implicit equation for a line in 2D - but
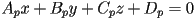 is the implicit equation for a plane (not a line) in 3D
is the implicit equation for a plane (not a line) in 3D
- implicit surfaces: planes and spheres
- in general, any algebraic equation in the variables
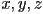 defines some implicit surface in 3D such that points
defines some implicit surface in 3D such that points 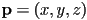 are on the surface iff the equation holds
are on the surface iff the equation holds - we will study two particular cases, planes and spheres
- as noted above, in general any plane in 3D can be written in the implicit form
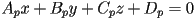
- this is the general form for a linear equation in three unknowns
- but what do the constants
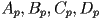 mean?
mean? - remember that in 2D a line is an object with two DoF, and these constants can be considered do define (1) the orientation of the line and (2) the perpendicular distance from the line to the origin
- that helped us to see that the 2D line equation
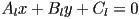 could be rewritten in vector form as
could be rewritten in vector form as 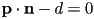 with
with 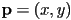 , a point on the line
, a point on the line 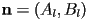 a normal vector to the line, and
a normal vector to the line, and 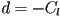 with
with 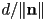 the perpendicular distance from the line to the origin
the perpendicular distance from the line to the origin- note that the selection of these constants is not unique for any given line
- after all, a line has only 2 DoF but we have three numbers to play with
- the reason for this is that if
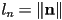 is the length of the normal vector, then
is the length of the normal vector, then 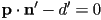 is a different equation for the same line where
is a different equation for the same line where 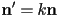 and
and  for any
for any 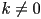
- we can follow the same approach to understand the implicit line equation in 3D
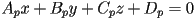 can be rewritten in vector form as
can be rewritten in vector form as 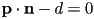 with
with 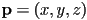 a point on the plane,
a point on the plane,  the 3D normal vector to the plane, and
the 3D normal vector to the plane, and 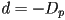 with
with 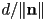 again the perpendicular distance from the plane to the origin
again the perpendicular distance from the plane to the origin- the exact same type of reasoning about DoF again applies here, and shows that a plane is an object with 3 DoF
- two of those can be considered to give the orientation of the plane
- (observe that the orientation of a plane is entirely defined by the direction of
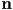 , but independent of
, but independent of 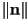 as long as
as long as  )
) - the remaining DoF is again the distance from the plane to the origin
- recall that in 2D the implicit equation for a circle with center
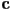 and radius
and radius 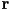 could be written
could be written 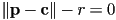
- this exact same equation is also the implicit form for a sphere in 3D with
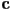 the 3D center of the sphere and
the 3D center of the sphere and 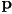 a 3D point on the sphere
a 3D point on the sphere
- in 2D, besides the implicit form for curves, we also had the parametric and procedural forms
- these are also important in 3D, but again they apply primarily to surfaces in this case
- we will briefly look at the parametric form for surfaces in 3D
- in 2D,
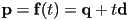 was a parametric form for the line through point
was a parametric form for the line through point  parallel to the vector
parallel to the vector 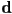
- in 3D,
 with
with 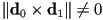 is the parametric form for a plane through 3D point
is the parametric form for a plane through 3D point 
- the main difference is now
 takes two parameters instead of one
takes two parameters instead of one - a little thought will reveal that the plane contains the point
 and has normal vector
and has normal vector 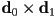
Triangles and Barycentric Interpolation in 3D
- one special surface that we will study in a little more detail is the triangle
- technically, the surface of a triangle in 3D is just a plane with extents limited to the edges of the triangle
- if a triangle is specified by giving the three 3D vertices
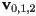 in order, then as we may compute
in order, then as we may compute 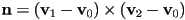 as the normal vector to the plane containing it
as the normal vector to the plane containing it

- the triangle is degenerate (all three vertices are on a single line) iff

- by this definition,
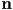 is pointing towards you exactly when the vertices appear to be in CCW order, and away from you when the vertices appear in CW order
is pointing towards you exactly when the vertices appear to be in CCW order, and away from you when the vertices appear in CW order - barycentric interpolation works the same in 3D as in 2D: if
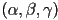 are the barycentric coordinates of a 3D point
are the barycentric coordinates of a 3D point 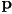 with respect to the triangle with 3D vertices
with respect to the triangle with 3D vertices 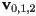 then the 3D Cartesian coordinates of
then the 3D Cartesian coordinates of 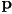 are
are 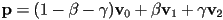
- how to go the other way—to find
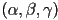 given
given 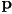 and
and 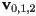 ?
?- it turns out that the following equations work
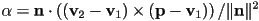


- derivation in Shirley and Marschner 3rd Ed p. 49
- Be careful: these are the barycentric coordinates for 3D point
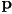 with respect to 3D triangle
with respect to 3D triangle 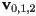 , but often (for example, in triangle rasterization) we end up projecting 3D triangles into 2D before working with barycentric coordinates. We covered 2D barycentric coordinate computations in L9.
, but often (for example, in triangle rasterization) we end up projecting 3D triangles into 2D before working with barycentric coordinates. We covered 2D barycentric coordinate computations in L9.
Curves in 3D
- so if surfaces in 3D take the role of curves in 2D, what about curves in 3D?
- curves (one-dimensional objects) in 3D, and are called space curves
- imagine a wire bent into a 3D shape; this is an approximation of a space curve
- the implicit form for a curve in 3D generally requires two algebraic equations
- for example, the implicit form for a line in 3D can be given with the two equations


- these are just two planes—the line is the intersection of the planes
- how many DoF does a line have in 3D?
- well, each plane has 3 DoF, so
 , but this is not quite right
, but this is not quite right - the reason is that if we rotate either plane about their intersection line, we still have the same line
- thus lines in 3D have
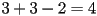 DoF
DoF
- we will generally not use implicit forms for curves in 3D
- the parametric form for a curve in 3D is exactly the same as in 2D:
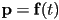 , but now
, but now 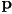 is 3D, so here
is 3D, so here  is
is  (for a 2D curve it was
(for a 2D curve it was 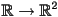 )
)- for example, a 3D line segment from 3D point
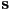 to 3D point
to 3D point 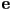 is just
is just 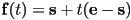 , with
, with 
- and a 3D ray starting at point
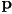 with direction vector
with direction vector 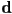 is
is 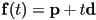 with
with 
Ray Intersection
- in 2D we mainly studied the intersection of pairs of curves (for example, two line segments)
- in 3D we can consider more possibilities:
- the intersection of two surfaces is generally one or more curves
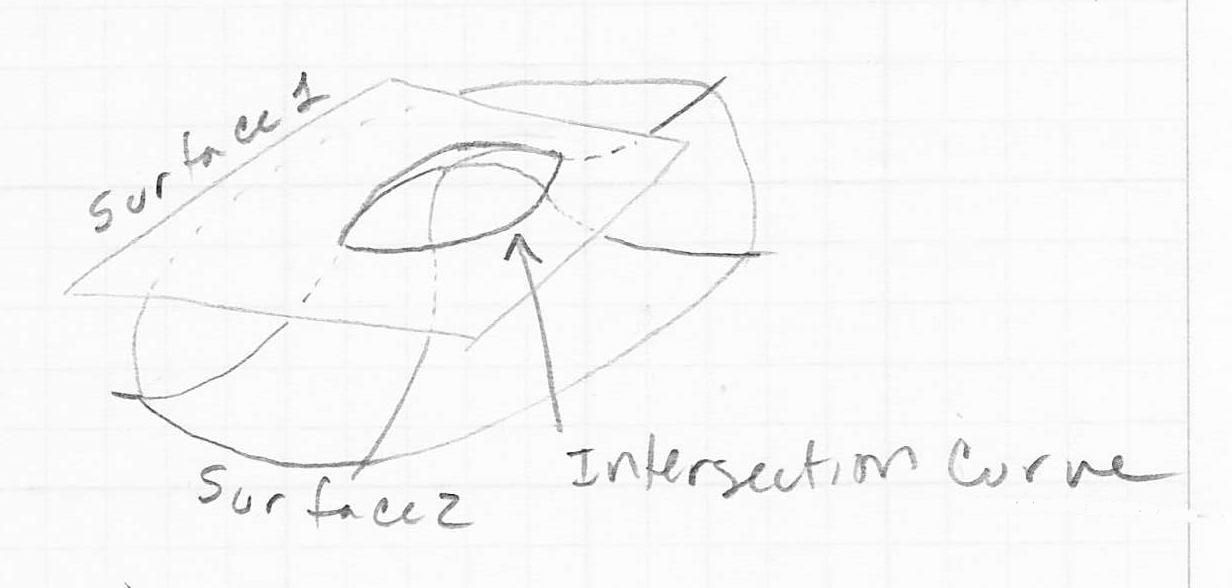
- the intersection of a curve and a surface is generally one or more points

- two curves have to be set up just right to intersect at all, but if they do, the result is generally one or more points
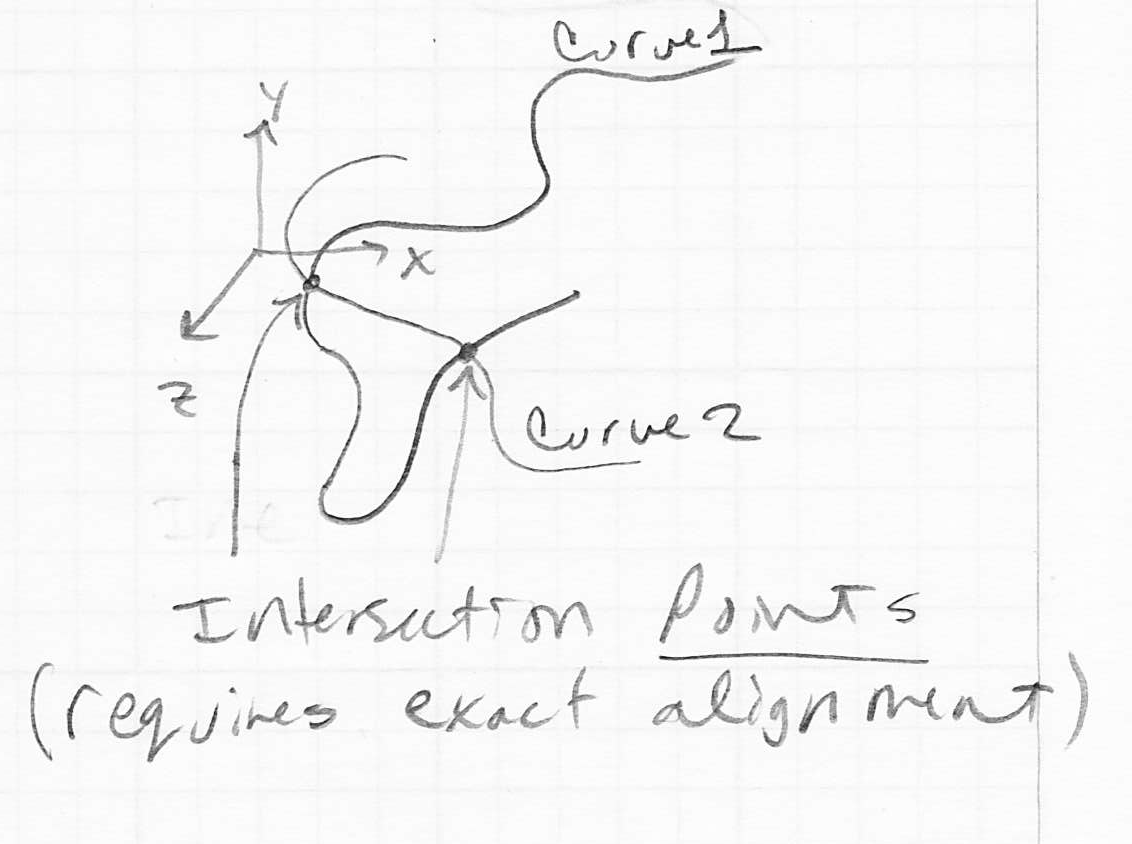
- all of those statements used the word “generally”, because there are exceptions—for example, two surfaces could be coincident (exactly on top of each other), in which case their intersection is a surface, not a curve
- 3D intersections are very useful, but we will not study the general case
- we will focus on one important situation: intersecting a 3D ray with various 3D surfaces
- this shows up in several different places in graphics, including ray tracing and picking in 3D (we will study both of these later in the course)
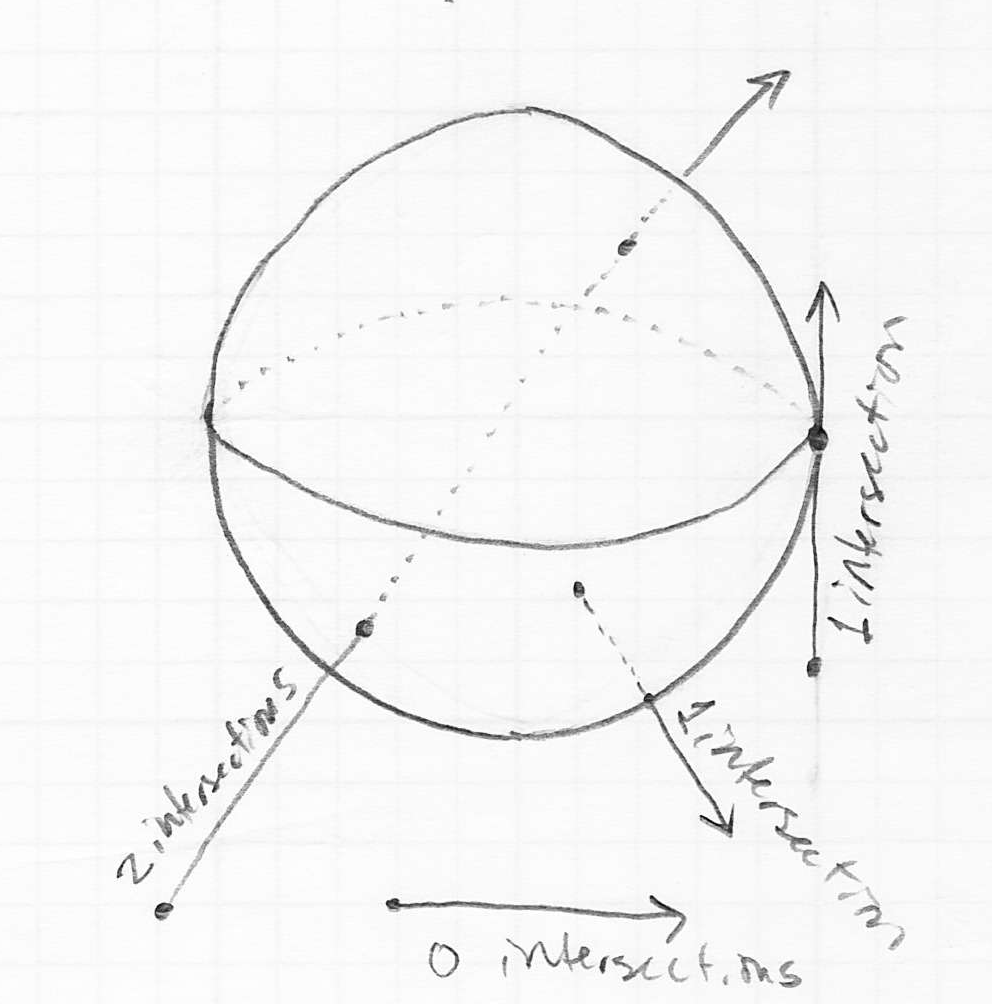
- ray/sphere intersection
- as a warm-up, let’s consider the intersection of a ray and a sphere in 3D
- one place this is useful in practice is when using spherical bounding volumes (we will study these later)
- note there are really two questions:
- how many intersection points are there (the answer can be 0, 1, or 2)
- if there is one or more intersection points, what are their coordinates?
- we will set up the math using the parametric form for a 3D ray given its 3D start point
 and 3D direction vector
and 3D direction vector 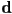 :
: 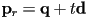
- and we will use the implicit form for a 3D sphere with center
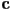 and radius
and radius  :
: 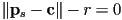
- the key insight is just that at any intersection point
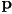 , it must be the case that
, it must be the case that 
- thus we can write a single equation in
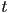 by substituting the expression for
by substituting the expression for  (a point on the ray as a function of
(a point on the ray as a function of 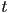 ) for
) for 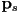 (a point on the sphere) in the sphere equation:
(a point on the sphere) in the sphere equation: 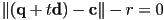
- we then rearrange this to see that it is really a quadratic equation in
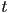 :
: 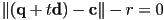

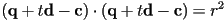
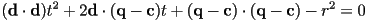
- remember, everything here is a constant except
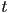
- if we define
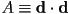

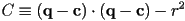
- then we know that the solutions are given by the quadratic formula

- there are no (real) solutions when the discriminant
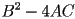 is negative (this corresponds to no intersection)
is negative (this corresponds to no intersection) - there is one solution when the discriminant is zero (this corresponds to the ray being exactly tangent to the sphere)
- there are up to two solutions when the discriminant is positive
- in this case there are two distinct real solutions for
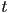 , however, one or both may be less than zero, corresponding to an intersection on the line through the ray but before the start of the ray
, however, one or both may be less than zero, corresponding to an intersection on the line through the ray but before the start of the ray
- ray/plane intersection
- the intersection of a ray and a plane may be similarly formulated
- now, there is either 0, 1, or
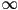 intersection points
intersection points- 0 when the ray is parallel but not coincident with the plane, or when the line through the ray intersects the plane before the start of the ray
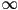 when the ray is coincident (“in”) the plane
when the ray is coincident (“in”) the plane- 1 otherwise
- we again take the parametric form for a ray given its start point
 and direction vector
and direction vector 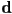 :
: 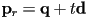
- and the implicit form for a plane with normal vector
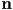 and perpendicular distance
and perpendicular distance  from the origin:
from the origin: 
- plug the first into the second:
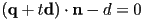
- and solve for
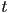 :
: 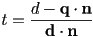
- the case where the denominator
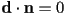 corresponds to the ray being parallel to the plane, and thus intersecting in either 0 or
corresponds to the ray being parallel to the plane, and thus intersecting in either 0 or 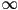 points (we generally don’t care to differentiate which)
points (we generally don’t care to differentiate which) - otherwise, there is a single unique (real) solution for
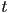 ; if it is non-negative then the ray and plane intersect
; if it is non-negative then the ray and plane intersect
- ray/triangle intersection
- ray/triangle intersection is a very common operation in graphics, because, as we know, in many systems triangle meshes form the basic representation of surfaces
- again let the ray be given as its 3D start point
 and direction vector
and direction vector 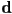 :
: 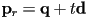
- let the triangle be given by its 3D vertices
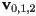
- the problem can be solved in a number of ways, but we care about speed here
- think about picking in 3D: the user has clicked the mouse on a scene composed of a large number of triangles
- this is generally converted into a ray/triangle intersection problem—the ray is computed based on both the click point and the current viewpoint
- there are ways to accelerate the process, but the basic idea is to check the intersection of the ray with every triangle
- we will study this in more detail later on
- forgetting about efficiency for a moment, we can get a working algorithm by combining a few things we already know how to do:
- compute
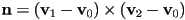 , the normal to the plane containing the triangle
, the normal to the plane containing the triangle - compute
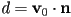 , the perpendicular distance from the origin to the plane containing the triangle scaled by
, the perpendicular distance from the origin to the plane containing the triangle scaled by 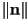 (this works because
(this works because  is a point known to be in the plane)
is a point known to be in the plane) - compute the
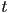 value at the intersection of the ray and plane
value at the intersection of the ray and plane - if there is no intersection, then exit
- if there is an intersection, say at
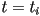 , then compute the coordinates of the intersection point as
, then compute the coordinates of the intersection point as 
- compute the barycentric coordinates
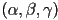 of
of 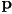 with respect to the triangle, using the equations given earlier in this lecture
with respect to the triangle, using the equations given earlier in this lecture - the ray intersects the triangle iff
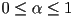 and
and 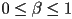 and
and 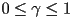
- in practice, an optimized version of this process is used
- first observe that if
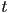 is the coordinate of the intersection point along the ray and
is the coordinate of the intersection point along the ray and  are the barycentric coordinates of the intersection point, then we can equate the Cartesian coordinates of each like this:
are the barycentric coordinates of the intersection point, then we can equate the Cartesian coordinates of each like this: 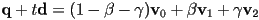
- that can be rewritten as
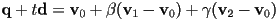
- we have lost
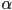 , but it was a function of
, but it was a function of 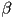 and
and 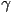 anyway,
anyway, 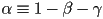
- now the conditions on the point being inside the triangle are
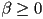 ,
, 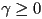 , and
, and 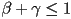
- this is actually a system of three equations in three unknowns
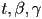 because it is 3D vector equation
because it is 3D vector equation - thus, we have the same number of equations as unknowns, and we can solve for
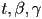
- one derivation, using Cramer’s rule, is in the text, Shirley & Marschner 3rd Ed. p. 78
- let
- now define
- or, equivalently as vectors
- then using
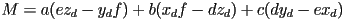
- or equivalently in vector form
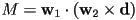 and
and - common sub-expressions, such as
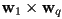 , can be calculated first
, can be calculated first - the denominator is the same in all cases—it’s zero iff the ray is parallel to the plane of the triangle, so check that first
- there are a few more options to “early out” of the routine, which speeds up handling non-intersecting triangles (usually the common case)
- you can compute
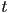 first, and if it’s negative, return false immediately
first, and if it’s negative, return false immediately - then once you compute the first barycentric coord, say
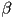 , you can check
, you can check 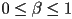 , and if not, then return false
, and if not, then return false
Next Time
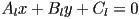 is the implicit equation for a line in 2D
is the implicit equation for a line in 2D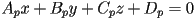 is the implicit equation for a plane (not a line) in 3D
is the implicit equation for a plane (not a line) in 3D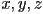 defines some implicit surface in 3D such that points
defines some implicit surface in 3D such that points 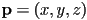 are on the surface iff the equation holds
are on the surface iff the equation holds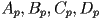 mean?
mean?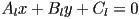 could be rewritten in vector form as
could be rewritten in vector form as 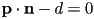 with
with 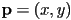 , a point on the line
, a point on the line 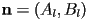 a normal vector to the line, and
a normal vector to the line, and 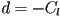 with
with 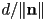 the perpendicular distance from the line to the origin
the perpendicular distance from the line to the origin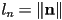 is the length of the normal vector, then
is the length of the normal vector, then 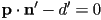 is a different equation for the same line where
is a different equation for the same line where 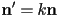 and
and  for any
for any 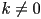
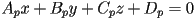 can be rewritten in vector form as
can be rewritten in vector form as 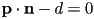 with
with 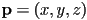 a point on the plane,
a point on the plane,  the 3D normal vector to the plane, and
the 3D normal vector to the plane, and 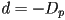 with
with 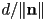 again the perpendicular distance from the plane to the origin
again the perpendicular distance from the plane to the origin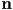 , but independent of
, but independent of 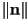 as long as
as long as  )
)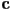 the 3D center of the sphere and
the 3D center of the sphere and 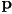 a 3D point on the sphere
a 3D point on the sphere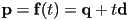 was a parametric form for the line through point
was a parametric form for the line through point  parallel to the vector
parallel to the vector 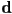
 with
with  is the parametric form for a plane through 3D point
is the parametric form for a plane through 3D point 
 takes two parameters instead of one
takes two parameters instead of one and has normal vector
and has normal vector