Computer Graphics (CS 4300) 2010S: Lecture 9
Today
- triangle mesh data structures
- barycentric coordinates
- rasterizing triangles
Triangle Mesh Data Structures
- often want to store a set of triangles together which represent the tessellation of some polygon (2D) or surface (3D)
- simplest datastructure is just a list or (typically) array of independent triangles
- in 2D, we can store the coordinates for each triangle vertex using e.g. two floating point numbers
- total storage for independent tris:
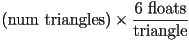
- because meshes are usually used to store contiguous tessellations, i.e. where many triangles share edges and vertices, storing all three vertices explicitly for each triangle can be a waste of space
- also, storing independent triangles does not enforce any mesh connectivity: to move a shared vertex, the programmer must find all triangles which touch that vertex and move them each independently
- the next simplest datastructure is an array of indexed triangles where each triangle is specified by three integer indices into a separate vertex array
- total storage for indexed independent tris:
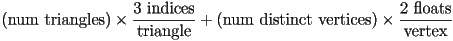
- this can save space when at least some triangles share common vertices
- also solves problem of editing a shared vertex
- can do better still
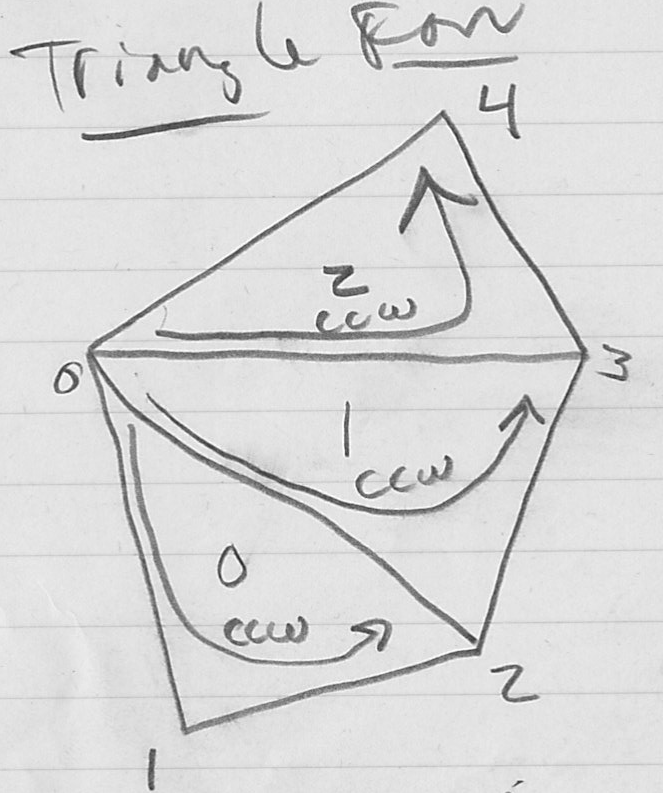
- recall the triangle fan that resulted from triangulation of a convex poly
- three vertices for first triangle
- only one vertex per triangle for all the rest
- vertices can either be given directly or indexed into a vertex array
- a triangle fan is thus an array of
 vertices which defines a corresponding mesh of
vertices which defines a corresponding mesh of 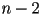 triangles
triangles - each triangle
 has vertices
has vertices  in CCW order
in CCW order
- triangle fans are commonly used not only for convex polys but also for any star shaped poly
- a poly is star shaped if there exists some point inside the poly from which all other points in the poly can be “seen”
- total storage for indexed triangle fan:
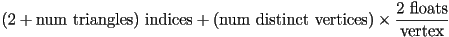
- note that triangle fans only work when all triangles share a common vertex
- a more general structure which again only uses
 vertices (or vertex indices) to represent
vertices (or vertex indices) to represent 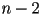 triangles is a triangle strip
triangles is a triangle strip- basic idea is to generate triangles one by one, each time reusing two vertices of the previous triangle
- so each triangle
 has vertices
has vertices 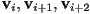
- however, these will be in CCW order if
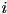 is even and CW order if
is even and CW order if 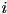 is odd
is odd
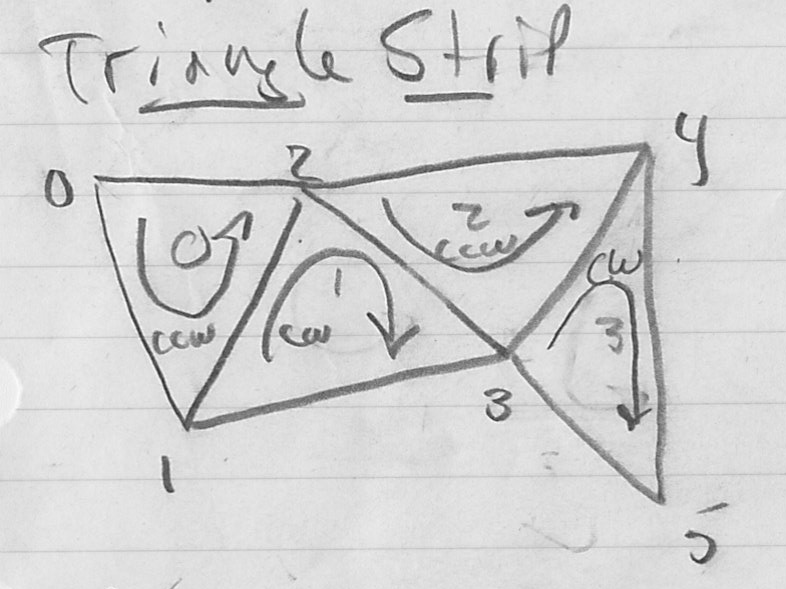
- common convention is to simply imply a reversal of the vertex order when reading/writing odd triangles from/to a strip
- total storage for triangle strip same as for triangle fan
- in practice, triangle meshes are often composed of multiple triangle arrays, each of which may be either independent triangles, a triangle fan, or a triangle strip. If indices are used, then a separate vertex array is also necessary.
Barycentric Coordinates
- recall the standard Cartesian (orthonormal) basis in 2D
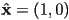 ,
, 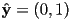
- any point
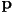 in 2D can be specified as a 2-dimensional vector
in 2D can be specified as a 2-dimensional vector 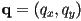 of its coordinates
of its coordinates - the interpretation is that the location of
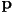 is given by origin of the coordinate frame plus a vector formed by the linear combination of the basis vectors weighted by
is given by origin of the coordinate frame plus a vector formed by the linear combination of the basis vectors weighted by 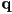
- if the origin is
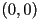 then this works out to
then this works out to 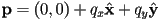
- this may seem tautological (true by construction), but that is because the standard basis at origin
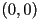 is a special case:
is a special case: 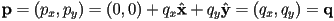
- however, we will need this level of formality to handle cases where the origin is not
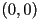 and/or the basis is not the standard basis
and/or the basis is not the standard basis
- now we will develop a coordinate system based on arbitrary 2D triangle
- the extension to 3D is straightforward; we will study it later in the course
- let the triangle vertices be
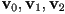 in CCW order
in CCW order - we will consider a barycentric coordinate frame to be defined as a local frame relative to the Cartesian world frame in which the triangle is specified
- define the barycentric basis vectors as
 and
and 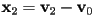
- note that these may be non-orthonormal; i.e., they may not be perpendicular and/or they may not be unit length
- define the origin of the barycentric frame to be the first triangle vertex
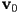
- now any 2-vector
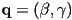 identifies a point relative to the barycentric basis and origin
identifies a point relative to the barycentric basis and origin - we can compute the corresponding world frame point
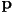 using the same formula as above:
using the same formula as above: 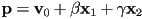
- note that this works for any
 , whether the point is inside or outside the triangle
, whether the point is inside or outside the triangle - thus, the barycentric basis and origin define a coordinate system for the entire 2D plane (as long as the triangle is not degenerate)
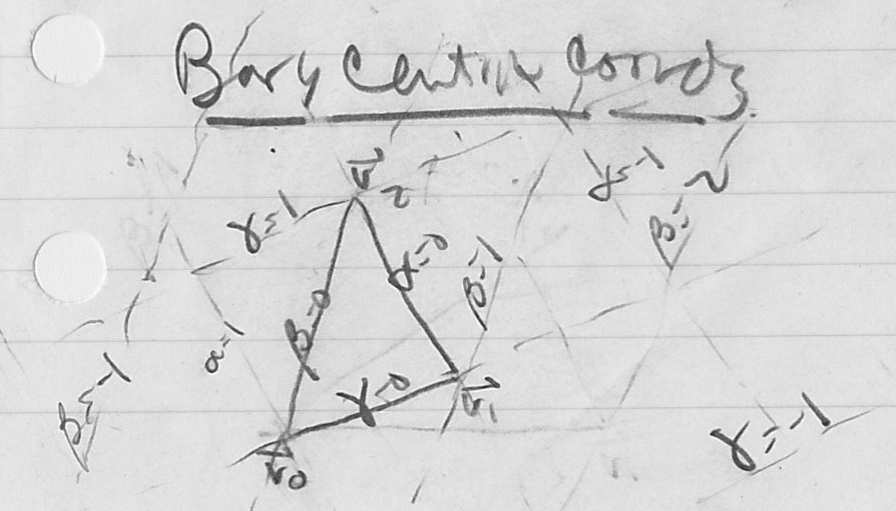
- one reason this is useful is that, with a little algebra, we can come up with simple conditions on
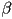 and
and 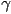 which hold if and only if
which hold if and only if 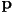 is inside the triangle
is inside the triangle - first, expand the above equation for
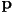 to use only the original triangle vertices:
to use only the original triangle vertices: 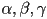 are called the barycentric coordinates of
are called the barycentric coordinates of 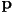
- interpretation:
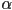 is a scaled distance from the edge
is a scaled distance from the edge  towards
towards 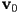
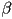 is a scaled distance from the edge
is a scaled distance from the edge 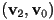 towards
towards 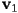
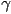 is a scaled distance from the edge
is a scaled distance from the edge 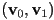 towards
towards 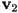
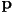 is inside the triangle (or on an edge) iff
is inside the triangle (or on an edge) iff- or, equivalently,
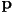 is on a vertex when the above conditions hold and any two of
is on a vertex when the above conditions hold and any two of 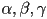 are both zero (this implies the remaining coordinate is 1)
are both zero (this implies the remaining coordinate is 1)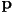 is on an edge when the above conditions hold and any one of
is on an edge when the above conditions hold and any one of 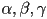 is zero (this implies the remaining two coordinates sum to 1)
is zero (this implies the remaining two coordinates sum to 1)- note that for all points on an edge, the two non-zero barycentric coordinates linearly interpolate from one vertex to the other
- in fact, barycentric coordinates also smoothly interpolate between all three vertices even in the interior of the triangle
- this is heavily used in graphics to smoothly interpolate coloring or shading information specified at vertices into the interior of a triangle
- recall that attributes such as color can be interpolated as well as coordinates
- especially in 3D, a common technique—called Gouraud shading—is to only calculate the effects of lighting in detail at the vertices, and then to interpolate through the interior
- this is not strictly correct, but it’s usually much faster than doing detailed calculations for every pixel, and it often looks fine as long as the triangles are relatively small
- we now know how to calculate the world-frame point
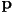 corresponding to barycentric coordinates
corresponding to barycentric coordinates 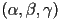 for a given triangle, but how to do the reverse?
for a given triangle, but how to do the reverse? - want to find
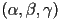 given
given 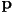 (whether or not
(whether or not 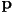 is in the triangle)
is in the triangle) - recall that “plugging in” the coordinates of a point into the implicit equation for a line in 2D returns a value proportional to the signed perpendicular distance from the point to the line
- i.e. if the equation of a line is
 then
then 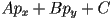 is proportional to the signed perpendicular distance from
is proportional to the signed perpendicular distance from 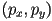 to the line
to the line - also recall that for any

 is also an equation for the same line
is also an equation for the same line - idea: first find any implicit equation for the line through each triangle edge, then apply a scaling factor to each so that the opposite vertex is at value 1 of the corresponding barycentric coordinate
- from before, one way to produce an implicit equation for a line through two points
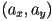 ,
,  is
is 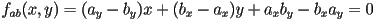
- let
 be the corresponding expression for barycentric coordinate
be the corresponding expression for barycentric coordinate 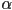
 be the corresponding expression for barycentric coordinate
be the corresponding expression for barycentric coordinate 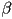
 be the corresponding expression for barycentric coordinate
be the corresponding expression for barycentric coordinate 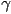
- now just need to calculate appropriate scaling factors
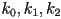 so that
so that - so these are just
- putting it all together, to find
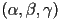 given
given 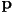 , whether or not
, whether or not 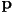 is in the triangle
is in the triangle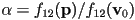
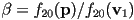
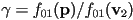
- where
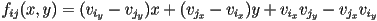 and the original triangle coordinates are
and the original triangle coordinates are 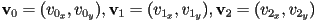
Rasterizing Triangles
- now that we know, for a given triangle with CCW vertices
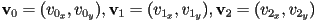
- how to determine the barycentric coordinates
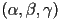 for any point
for any point 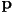 in world frame
in world frame - how to determine if
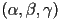 are inside the triangle
are inside the triangle - how to interpolate vertex attributes, e.g. colors, using barycentric coordinates
- a reasonable triangle rasterization algorithm, i.e. an algorithm that takes
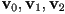 and turns on (or colors) the pixels inside the triangle, is simply
and turns on (or colors) the pixels inside the triangle, is simply ,
, 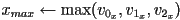
 ,
, 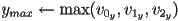
- for
 to
to 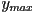
- for
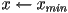 to
to 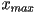
- compute barycentric coordinates
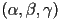 of
of 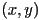
- if
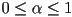 and
and 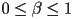 and
and 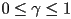
- turn on pixel
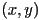
- or, if vertex colors
 ,
,  ,
, 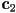 were given, set pixel
were given, set pixel 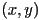 to color
to color 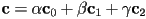
- runtime scales as the size of the bounding rectangle of the triangle
- reasonably fast in practice, especially if care is taken to implement all calculations incrementally, in the same spirit as we did for rasterizing a line segment
- another practical issue to deal with is rasterizing two triangles that share an edge
- in practice, want each screen pixel to be “owned” by at most one triangle
- translucent triangle rendering looks bad otherwise
- “single ownership” can be be accomplished in a careful implementation
Next Time
- reading on website
- rigid and non-rigid transformations in 2D
- homogeneous coordinates
- scene graphs
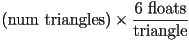
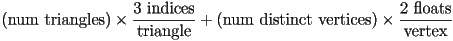
 vertices which defines a corresponding mesh of
vertices which defines a corresponding mesh of 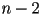 triangles
triangles has vertices
has vertices  in CCW order
in CCW order 
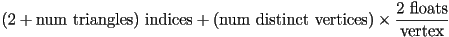
 has vertices
has vertices 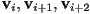
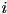 is even and CW order if
is even and CW order if 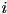 is odd
is odd 
