Lecture 7: Lists continued
Abstract Data Types.
Generic lists.
Lists in Java.
7.1 The Abstract Data Type
The IListOfBooks interface with its two implementations EmptyNode and ElementNode (see Lecture 6: Recursive unions: Lists) create a list-like structure, but not quite. We associate certain operations with a list, such as being able to add to it at specific positions, remove from it, traverse it, etc. But our current implementation has several design issues.
First, our way of creating a list is to cobble together one explicitly as shown in the examples.
partialListOfBooks = new ElementNode(new Book("HP 1", "J.K. Rowling", 1997, 19.99f), new ElementNode(new Book("HP 2", "J.K. Rowling", 1999, 29.99f), new ElementNode(new Book("HP 3", "J.K. Rowling", 2001, 10.99f), new EmptyNode())));
Secondly, there isn’t a good way to make helper methods (e.g. insert) non-public. This is because the IListOfBooks interface exposes all the operations on the nodes as public methods. We could create an abstract class and make insert a private method there, but then the ElementNode class would have to represent the rest field as an object of this abstract class, and its constructor would have to take in such an object as well. This somewhat breaks the illusion of there being an invisible abstract class that is handling some implementation details without exposing them in the interface.
What we need is a way to talk about a list of things as “one object” that hides all its implementation details and only exposes “list-level” operations. Thus we should be able to talk of a list as a data structure that offers these operations. At a high level, the concept of a data structure with typical operations expected from it is called an Abstract Data Type (ADT).
An ADT represents a data structure at a high-level and abstract way, only from the point of view of operations and not how the structure is actually implemented. This allows us to concentrate on the use of such a structure in a particular context. Thus when we talk about a list in general, we talk about its expected operations without specifying (right away) whether it is implemented as a linked list, or in some other way. If we do implement it as a linked list, the entire notion of a “node” (and therefore its interface, abstract and concrete implementations) is an internal detail and is not exposed as part of the list interface. This gives us more freedom to hide helper methods behind the ADT and expose only operations that make sense for a general list.
What would a List ADT contain? Any list stores data as a sequence, i.e. each piece of data in the list has the notion of a position. We would like to think of the following operations that are expected from a list-like structure:
Add an element to it at the beginning
Add an element to it at the end
Add an element to it in the middle (e.g. so that it occupies a specific position)
Count the number of elements in the list
Get the element at a specified position in the list
Remove an element from the list if it exists
7.1.1 Design of an Abstract Data Type
We can design an abstract data type as a set of functions that operate upon a list. Each function takes a list as input and returns an answer. In the case of list-changing operations (e.g. adding/removing), the function would return the resulting list.
In Java a possible implementation could look like the following:
public interface ListNode {} public class EmptyNode implements ListNode { public EmptyNode() {} } public class ElementNode implements ListNode { private Book data; private ListNode rest; public ElementNode(Book data, ListNode rest) { this.data = data; this.rest = rest; } public Book getBook() { return this.book;} public ListNode getRest() {return this.rest;} } public class ListOperations { public static ListNode addFront(ListNode head, Book b) {...} public static ListNode addBack(ListNode head,Book b) {...} public static ListNode add(ListNode head, int index, Book b) {...} public static int count(ListNode head) {...} public static Book get(ListNode head,int index) {...} public static ListNode remove(ListNode head,Book b) {...} }
The ListNode is an interface that defines the basic union type. It is implemented (as before) by the EmptyNode and the ElementNode classes. Since all of the functions are external to the nodes, we can implement them as static methods inside a separate class in Java.
An example of usage would be:
@Test public void testListUsage() { ListNode head = new EmptyNode(); Book book1 = new Book(...); Book book2 = new Book(...); Book book3 = new Book(...); //add some books head = ListOperations.addFront(head, book1); head = ListOperations.addBack(head, book2); head = ListOperations.add(head, 1, book3); //the list should be book1, book3, book2 assertEquals(3, ListOperations.count(head)); assertEquals(book3, ListOperations.get(head, 2)); ... }
This is a non-object-oriented design, similar to what we saw in Lecture 1. We have achieved some of the encapsulation that we expected, with ListNode representing the data and ListOperations encapsulating all the functions operating on the list. When we contrast the above test with our earlier implementation, we observe that creating a list is a simpler operation: we tell what we want to do ("add to the front") and the details of linking various list nodes is hidden inside the addFront function. These functions also enforce important invariants needed to maintain the integrity of the list, such as "the list ends with an EmptyNode object." The programmer who implements the test does not have to ensure this. Furthermore, helper methods can be made private in the ListOperations class, keeping its interface clean.
Another design could be the classic object-oriented design. Similar to the process earlier, we distill the list operations into an interface:
/** * This interface represents the List of books ADT */ public interface BookListADT { /** * Add a book to the front of this list * @param b the book to be added to the front of this list */ void addFront(Book b); /** * Add a book to the back of this list (so it is the last book in the list * @param b the book to be added to teh back of this list */ void addBack(Book b); /** * Add a book to this list so that it occupies the provided index. Index * begins with 0 * @param index the index to be occupied by this book, beginning at 0 * @param b the book to be added to the list */ void add(int index,Book b); /** * Return the number of books currently in this list * @return the size of the list */ int getSize(); /** * Remove the first instance of this book from this list * @param b the book to be removed */ void remove(Book b); /** * Get the (index)th book in this list * @param index the index of the book to be returned * @return the book at the given index * @throws IllegalArgumentException if an invalid index is passed */ Book get(int index) throws IllegalArgumentException; }
Note that in contrast to the IListOfBooks interface in Lecture 5: Union Data types, this interface represents a list, and not a list node (the list node is a union type, but we are thinking of a list as a single entity. Thus, a list is not a union).
In the following sections, we elaborate on the implementation of this OO-based design.
7.2 OO: Implement a list as an ADT
We keep the design similar to that in Lecture 5: Union Data types. We represent a node in the list with a BookListADTNode interface, and implement it as BookListADTElementNode and BookListADTEmptyNode classes respectively.
Now let us rethink the way we implement our list ADT. We could use such a list as follows:
BookListADT list = ...; //add one at beginning list.addFront(new Book("HP 2", "J.K. Rowling", 1998, 10.99f)); list.addFront(new Book("HP 1", "J.K. Rowling", 1997, 19.99f)); ...
Similar to the design above, we can now build a list progressively, one book at a time. However in this design, the client is keeping track of a "list object" that itself offers methods to manipulate it (instead of holding onto a head and using another class for the functions). This "list object" represents a list, and implements the BookListADT interface. This class uses the nodes and their functionality to maintain a list, all within it.
/** * This class implements the List of Books ADT */ public class BookListADTImpl implements BookListADT { ... }
7.2.1 Data
The following figure helps to visualize how this list will evolve when elements are added to it.
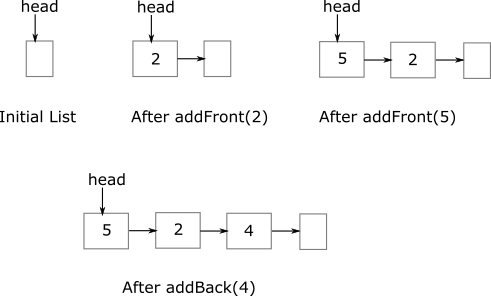
The list is initially empty. After 1 addition, it grows to having one non-empty node. If the list is printed at this point, it should print the contents of the node. After two more additions, the list changes to the last figure. If the list is printed at this point, it should print the contents of the three nodes.
Thus the list implementation must keep track of the current status of the list. This keeps changing as operations are used. The implementation keeps track of the current list as a BookListADTNode field.
public class BookListADTImpl implements BookListADT { private BookListADTNode head; //list is initialized to be empty public BookListADTImpl() { head = new BookListADTEmptyNode(); } }
As the operations are called, the identifier head changes to keep track of the resulting list. This effect is called mutation. You can think of the head variable changing as the object is used.
Mutation helps an object to record changes in itself as a result of operations. Note that none of the add methods returns anything: any changes they produce are recorded within the list object itself. Thus the results of such operations are not explicitly returned, but simply recorded in the fields of the calling object. This is called a side effect of the method.
7.2.2 Mutation and ADT
It is not required to use mutation to implement an ADT. Consider if we had chosen not to use mutation to implement this ADT. In that case, the BookListADT interface would be very similar to the ListOperations interface above, except the methods would not be static. Its usage would be:
BookListADT list = ...; Book book1 = new Book(...); Book book2 = new Book(...); Book book3 = new Book(...); //add some books list = list.addFront(book1); list = list.addBack(book2); list = list.add(1,book3); ...
The usage of "list" twice on each line makes it seem redundant. However one could implement the methods without mutation, returning a "fresh" list each time (one could keep track of the old and new list simultaneously). This style has some advantages in certain contexts.
With mutation the left hand side of the assignment statements is removed. The client simply specifies operations on the list, and when it requires the current status of the list, uses other methods (such as toString, get and count) to know different things about the result of the operations executed thus far.
Our preference for using mutation in this example has more to do with our overall vision of using the list (manipulate-but-store, return results when needed), rather than the concept of the ADT itself.
7.2.3 getSize() and toString
These methods in BookListADTImpl simply delegate to the corresponding methods in the node classes (count and toString).
7.2.4 Add to the front of the list
How should the list change if a new book is added to its front? If the list was empty, it would now have a new BookListADTElementNode object with the rest of the list as empty. If the list was not empty the new list would have a new BookListADTElementNode object with the rest being the list as before.
The list can delegate this work to the nodes, as all these operations have to do with individual nodes. As we have BookListADTEmptyNode and BookListADTElementNode we can allow dynamic dispatch to choose between these cases.
//In BookListADTImpl @Override public void addFront(Book b) { head = head.addFront(b); } //In BookListADTEmptyNode @Override public BookListADTNode addFront(Book book) { return new BookListADTElementNode(book, this); } //In BookListADTElementNode @Override public BookListADTNode addFront(Book book) { return new BookListADTElementNode(book, this); }
Notice the code in BookListADTImpl. It says “add b to the front of the current list, and update the result to be the new list.” The assignment statement mutates head.
7.2.5 Add to the back of the list
Adding to the back of the list is easier: the last node in the list is always an empty node. Thus BookListADTEmptyNode will create a new BookListADTElementNode that will store the new book, with the rest of the list being empty. In other words, it will be identical to its addFront method as above.
Since an BookListADTElementNode object can never be the end of a list, it has to simply “pass on” to the rest of the list.
//In BookListADTImpl @Override public void addBack(Book b) { head = head.addBack(b); } //In BookListADTEmptyNode @Override public BookListADTNode addBack(Book book) { return addFront(book); } //In BookListADTElementNode @Override public BookListADTNode addBack(Book book) { this.rest = this.rest.addBack(book); return this; }
Why must this.rest mutate in BookListADTElementNode? Consider that before adding, this.rest may be an BookListADTEmptyNode object. After adding, it will change to a BookListADTElementNode object as returned by the addBack method of the BookListADTEmptyNode class. This is also the reason this.head of BookListADTImpl must also mutate.
7.2.6 Add to a specific position of the list
Consider a visualization of adding something so that it occupies a specific position. The following figure shows adding a new element so that it occupies index 2 (assuming positions start at 0).

Do Now!
Try to reason how this operation can work. Can you add to the front of some list?
Upon close inspection it can be observed that the new element must be added to the front of the list beginning with 4. Furthermore, the rest field of the node with 2 must mutate so that it now refers to this new list. Putting this another way, we must add the new element to the front of the list beginning with the node currently at the required index, and mutate the node just behind it.
We start with the insight that if the position to be added is 0, we know how to do this (it is the same as adding to the front of the list). Adding at position 2 in the list starting at 5 is the same as adding at position 1 in the list starting at 2, or adding at position 0 (i.e. in front) in the list starting at 4. Thus if we haven’t reached the front of the correct list yet, we keep adding to the “rest” of the list.
//In BookListADTImpl @Override public void add(int index, Book b) { head = head.add(index, b); } //In BookListADTElementNode @Override public IListOfBooks add(int index, Book book) { if (index == 0) { //add to the front of this list return addFront(book); //add in front of this list and return the updated list } else { this.rest = this.rest.add(index - 1, book); //add at index-1 in the rest of the list return this; } }
Notice the critical line this.rest = this.rest.add(index - 1, book);. When index is 1 it will advance to the rest list which will add the book and return the updated list. Although the line looks confusing as it has recursion and mutation on it, expressing it in plain language helps us understand what it is actually accomplishing (add an element to the rest of the list, and let the result be the new rest of the list).
What about BookListADTEmptyNode? The only valid index at which something could be added would be 0.
7.2.7 Getting the ith book
Getting the book at a specific index is similar to adding a book there: one must get to the appropriate place in the list and return the book at that node. Like before “the 3rd book in the list starting at the first node is the same as the 2nd book in the list started at the second node, and so on.” We also need to account for the possibility that the index is invalid. This translates to the following implementation:
//In BookListADTImpl @Override public Book get(int index) throws IllegalArgumentException{ if ((index >= 0) && (index < getSize())) { return head.get(index); } else throw new IllegalArgumentException("Invalid index"); } //In BookListADTElementNode @Override public Book get(int index) throws IllegalArgumentException{ if (index == 0) return this.book; return this.rest.get(index - 1); } //In BookListADTEmptyNode @Override public Book get(int index) throws IllegalArgumentException { throw new IllegalArgumentException("Wrong index"); //it should never get here if index is valid! }
7.2.8 Removing a book
A book to be removed can only be in an BookListADTElementNode object, if it exists in the list. When this node is found, something similar to add(int index, Book b) happens. The rest of the previous node must mutate to refer to the rest of the list for this node. This will effectively bypass and remove this node.
Much like add(int index, Book b) it helps to think about getting to a stage where one must remove the beginning node of a list. The list after such a deletion is simply the rest of the list. We will mutate the rest field like before.
//In BookListADTImpl @Override public void remove(Book b) { head = head.remove(b); } //In BookListADTElementNode @Override public IListOfBooks remove(Book book) { if (this.book.equals(book)) { return this.rest; //return the rest of the list as the result of deletion } else { this.rest = this.rest.remove(book); //the rest is whatever the //result of removing it from the rest will be return this; //this is now the list as a result of deletion, so return it } }
7.2.9 Tests
The advantages of designing a list as an ADT are apparent when we write code that uses it. Here is what the tests look like:
public class BookListADTTest { @Test public void testListADT() { BookListADT list = new BookListADTImpl(); assertEquals("", list.toString()); //add one at beginning list.addFront(new Book("HP 2", "J.K. Rowling", 1998, 10.99f)); list.addFront(new Book("HP 1", "J.K. Rowling", 1997, 19.99f)); assertEquals("(Title: HP 1 Year: 1997 Price: 19.99)(Title: HP 2 Year: " + "1998 Price: 10.99)", list.toString()); //add to the end list.addBack(new Book("HP 3", "J.K. Rowling", 1999, 12.99f)); list.addBack(new Book("HP 4", "J.K. Rowling", 2001, 15.99f)); assertEquals("(Title: HP 1 Author: J.K. Rowling Year: 1997 Price: 19.99)"+ "(Title: HP 2 Author: J.K. Rowling Year: 1998 Price: 10.99)"+ "(Title: HP 3 Author: J.K. Rowling Year: 1999 Price: 12.99)"+ "(Title: HP 4 Author: J.K. Rowling Year: 2001 Price: 15.99)", list.toString()); assertEquals("HP 1", list.get(0).getTitle()); assertEquals("HP 2", list.get(1).getTitle()); assertEquals("HP 3", list.get(2).getTitle()); assertEquals("HP 4", list.get(3).getTitle()); list.remove(new Book("HP 3","J.K. Rowling", 1999,12.99f)); assertEquals("(Title: HP 1 Author: J.K. Rowling Year: 1997 Price: 19.99)"+ "(Title: HP 2 Author: J.K. Rowling Year: 1998 Price: 10.99)"+ "(Title: HP 4 Author: J.K. Rowling Year: 2001 Price: 15.99)", list.toString()); } }
As you can see one can operate on a list as if it were an object rather than having to explicitly keep track of the list. Specifically there is no mention of the BookListADTNode interface and the BookListADTElementNode and BookListADTEmptyNode classes. All the implementation details of the list are hidden from the client, which is good object-oriented design.
7.3 A list of anything
If we look carefully at the BookListADT we notice that none of the operations are book-specific. This is not surprising: the operations we desire from a list are irrespective of what that list contains. A list of numbers behaves the same way as a list of books or a list of images. Therefore it is reasonable to expect that if we created a list for strings, all its methods would look very similar to those in our BookListADTImpl implementation. How can we write a list in a way that is independent of what data is stored in it?
What we need is provided by generics in Java. Generics are classes or interfaces that specify operations but leave the type of data they work with unspecified. When we instantiate these generic classes we specify the actual type of data they work with.
7.3.1 The generalization of book list
In an attempt to make our BookListADT work with other types of data, we create an interface ListADT as follows:
/** * This interface represents a generic list. It is a generalization of the * BookListADT interface. * * We represent the type of data that this will work with a generic parameter * T. This is a placeholder for the actual data type. */ public interface ListADT<T> { /** * Add an object to the front of this list * @param b the object to be added to the front of this list */ void addFront(T b); /** * Add an object to the back of this list (so it is the last object in the * list * @param b the object to be added to teh back of this list */ void addBack(T b); /** * Add an object to this list so that it occupies the provided index. Index * begins with 0 * @param index the index to be occupied by this object, beginning at 0 * @param b the object to be added to the list */ void add(int index, T b); /** * Return the number of objects currently in this list * @return the size of the list */ int getSize(); /** * Remove the first instance of this object from this list * @param b the object to be removed */ void remove(T b); /** * Get the (index)th object in this list * @param index the index of the object to be returned * @return the object at the given index * @throws IllegalArgumentException if an invalid index is passed */ T get(int index) throws IllegalArgumentException; }
As the above code shows we define a generic interface ListADT<T> where T is a placeholder for the actual type of objects that this list will hold. We write all method signatures by writing T every time we mean “the object in the list” (for example, get returns an object of type T).
Much like the BookListADT, an implementation of ListADT will keep track of the node for the list within it. So we must create generic versions of BookListADTNode, BookListADTEmptyNode and BookListADTElementNode which we name GenericListADTNode, GenericEmptyNode and GenericElementNode respectively.
/** * This represents an empty node of the generic list implementation. */ public class GenericEmptyNode<T> implements GenericListADTNode<T> { @Override public int count(){ return 0; } @Override public GenericListADTNode<T> addFront(T object) { return new GenericElementNode(object, this); } @Override public GenericListADTNode<T> addBack(T object) { return addFront(object); } @Override public GenericListADTNode<T> add(int index, T object) throws IllegalArgumentException { if (index == 0){ return addFront(object); } throw new IllegalArgumentException("Invalid index to add an element"); } @Override public GenericListADTNode<T> remove(T object) { return this; //cannot remove from nothing! } @Override public T get(int index) throws IllegalArgumentException { throw new IllegalArgumentException("Wrong index"); } @Override public String toString() { return ""; } }
/** * This is a non-empty node in a generic list. It contains the object data * and the rest of the list */ public class GenericElementNode<T> implements GenericListADTNode<T> { private T object; private GenericListADTNode<T> rest; public GenericElementNode(T p, GenericListADTNode<T> rest) { this.object = p; this.rest = rest; } @Override public int count() { return 1 + this.rest.count(); } @Override public GenericListADTNode<T> addFront(T object) { return new GenericElementNode(object, this); } @Override public GenericListADTNode<T> addBack(T object) { this.rest = this.rest.addBack(object); return this; } @Override public GenericListADTNode<T> add(int index, T object) { if (index == 0) { return addFront(object); } else { this.rest = this.rest.add(index - 1, object); return this; } } @Override public GenericListADTNode<T> remove(T object) { if (this.object.equals(object)) { return this.rest; } else { this.rest = this.rest.remove(object); return this; } } @Override public T get(int index) throws IllegalArgumentException{ if (index == 0) return this.object; return this.rest.get(index - 1); } @Override public String toString() { String objstring = this.object.toString(); String rest = this.rest.toString(); if (rest.length() > 0) return objstring + " " + rest; else return objstring; } }
In Java only non-primitive types can be used with generics. That is, one cannot create ListADT<int>. If we wish to create a list of integer numbers, we can use the wrapper class Integer.
Finally we can implement the ListADT interface in the ListADTImpl class.
/** * This is the implementation of a generic list. Specifically it implements * the ListADT interface */ public class ListADTImpl<T> implements ListADT<T> { private GenericListADTNode<T> head; public ListADTImpl() { head = new GenericEmptyNode(); } @Override public void addFront(T b) { head = head.addFront(b); } @Override public void addBack(T b) { head = head.addBack(b); } @Override public void add(int index, T b) { head = head.add(index, b); } @Override public int getSize() { return head.count(); } @Override public void remove(T b) { head = head.remove(b); } @Override public T get(int index) throws IllegalArgumentException{ if ((index >= 0) && (index < getSize())) { return head.get(index); } else throw new IllegalArgumentException("Invalid index"); } @Override public String toString() { return "(" + head.toString() + ")"; } }
7.3.2 Testing the ListADT implementation
We can now create examples of ListADTImpl objects and test them.
public class ListADTTest { private ListADT<String> stringList; @Before public void setup() { stringList = new ListADTImpl<String>(); } @Test public void testStringList() { stringList.addFront("won"); stringList.addFront("Patriots"); stringList.addBack("Super"); stringList.addBack("Bowl"); stringList.add(2, "the"); assertEquals("(Patriots won the Super Bowl)", stringList.toString()); assertEquals(5, stringList.getSize()); assertEquals("Super", stringList.get(3)); stringList.remove("Patriots"); stringList.addFront("Falcons"); stringList.add(1, "did"); stringList.add(2, "not"); stringList.remove("won"); stringList.add(3, "win"); assertEquals("(Falcons did not win the Super Bowl)", stringList.toString()); assertEquals(7, stringList.getSize()); } }
When we declare the variable stringList we must specify what kind of a list it can refer to.
When we instantiate the list object in setup() we must specify what kind of objects the list can hold.
We see that for the stringList object, java replaces the generic parameter T with String. Thus the get method returns a String object, while the addFront, addBack and add methods take String arguments.
All parameters to methods of stringList change from T to String.
7.4 Higher-order functions on lists
Recall the three higher-order functions from Lecture 6: Recursive unions: Lists: map, fold/reduce and filter. As we now have a list available as an ADT, we can now conceptualize higher-order functions on them.
7.4.1 Map
A map is a higher-order function that converts a list that contains data of one type, into a list of identical structure that contains data of another type. Each element in the resulting list can be thought of as a conversion of the corresponding element in the original list. Thus the map higher-order function requires a function that converts from the source to the destination type.
We can define a map on our ListADT-type objects as follows:
public interface ListADT<T> { ... /** * A general purpose map higher order function on this list, that returns * the corresponding list of type R. * @param converter the function that converts T into R * @param <R> the type of data in the resulting list * @return the resulting list that is identical in * structure to this list, but has data of type R */ <R> ListADT<R> map(Function<T,R> converter); }
Specifically, we use Java’s Function interface to define a method that converts an object from type T into type R. This signature allows us to map our list into a list of any other type allowed by Java’s generics.
How do we define it? Similar to other operations, the ListADTImpl implementation simply delegates to a (map) method in the GenericListADTNode-type objects. One minor problem is that our method is supposed to return a ListADT<R> object, while the map in the nodes will return a GenericListADTNode<R> object. Therefore we write a private constructor that encapsulates the returning (head) node into a ListADTImpl object.
public class ListADTImpl<T> implements ListADT<T> { private GenericListADTNode<T> head; ... //a private constructor that is used internally (see map) private ListADTImpl(GenericListADTNode<T> head) { this.head = head; } @Override public <R> ListADT<R> map(Function<T,R> converter) { return new ListADTImpl(head.map(converter)); } }
The above usage necessitates the following addition in the nodes:
//In GenericListADTNode /** * A general map higher order function on nodes. This * returns a list of identical structure, but each data * item of type T converted into R using the provided * converter method. * @param converter the function needed to convert T * into R * @param <R> the type of the data in the returned list * @return the head of a list that is structurally * identical to this list, but contains data * of type R */ <R> GenericListADTNode<R> map(Function<T,R> converter); //In GenericElementNode @Override public <R> GenericListADTNode<R> map(Function<T,R> converter) { ... } //In GenericEmptyNode @Override public <R> GenericListADTNode<R> map(Function<T,R> converter) { ... }
The implementation in GenericEmptyNode is trivial: the mapped list is also empty.
//In GenericEmptyNode @Override public <R> GenericListADTNode<R> map(Function<T,R> converter) { return new GenericEmptyNode(); }
How do we create a non-empty mapped list? We express this operation in terms of itself: Starting from this node, the mapped list has the first node containing the data converted from this node, followed by the rest of the mapped list. This leads to the following straightforward implementation:
//In GenericElementNode @Override public <R> GenericListADTNode<R> map(Function<T,R> converter) { return new GenericElementNode( converter.apply(this.object), this.rest.map(converter)); }
We can test this map implementation using a test that converts a list of strings into a list of integers:
@Test public void testMap() { // convert the list of strings above to a list that // contains the length of each word in the list String sentence = "The quick brown fox jumps over the lazy dog"; String []words = sentence.split("\\s+"); for (String w:words) { stringList.addBack(w); } ListADT<Integer> wordLengths = stringList.map(s->s.length()); assertEquals(stringList.getSize(), wordLengths.getSize()); for (int i=0;i<words.length;i++) { assertEquals(words[i].length(), (int)wordLengths.get(i)); } }
Do Now!
Think about how to implement fold and filter.
7.5 Lists in Java
The ListADT interface and its ListADTImpl implementation of a generic linked list are very similar to something that already exists in Java. Java defines a List<T> interface for all operations on lists. Look at the List documentation. This interface is implemented as a linked list by the LinkedList<T> class.
7.5.1 The LinkedList<T> class
Here is an example of the above test, but using Java’s List<T> interface and LinkedList<T> class.
@Test public void testStringLinkedList() { List<String> llist = new LinkedList<String>(); llist.add(0, "won"); llist.add(0, "Patriots"); llist.add("Super"); llist.add("Bowl"); llist.add(2, "the"); assertEquals("[Patriots, won, the, Super, Bowl]", llist.toString()); assertEquals(5, llist.size()); assertEquals("Super", llist.get(3)); llist.remove("Patriots"); llist.add(0, "Falcons"); llist.add(1, "did"); llist.add(2, "not"); llist.remove("won"); llist.add(3, "win"); assertEquals("[Falcons, did, not, win, the, Super, Bowl]", llist.toString()); assertEquals(7, llist.size()); }
Notice the minor differences: List<T> has no addFront, it simply uses add with an index of 0. The toString() also produces a slightly different string.
Do Now!
The ListADTImpl internally tracks an GenericListADTNode object to implement its operations. Think about how you will implement our ListADT interface by using Java’s LinkedList class.
7.5.1.1 Printing a list as before
Let us write a method that returns a string that is like the one we wrote in the BookListADTImpl: each object is enclosed in parentheses and objects are separated by spaces. The test for it would be:
@Test public void testToString() { List<String> llist = new LinkedList<String>(); llist.add("I"); llist.add("am"); llist.add("a"); llist.add("teacher"); assertEquals("(I) (am) (a) (teacher)", StringListUtils.toString(llist)); }
Since we cannot add a method to Java’s LinkedList class, we write a static method in a helper class called StringListUtils.
We can implement it recursively as before: “the string representation of the list is the string representation of the first element in the list, and appended to it is the string representation of the rest of the list.” Unfortunately we do not know how LinkedList is implemented in Java and furthermore, it has been designed so that we would not have access to its internal nodes. But we do have the ability to get the element at any position using the get method.
So we could change the definition as: “for each position in the list, create a string representation of object at that position and append them all to each other.” We can still implement this recursively. We use an argument that counts the position starting from 0, and then recursively call the method with the next position.
public static String toString(List<String> list) { return toStringRec(list, 0); } private static String toStringRec(List<String> list, int index) { if (index >= list.size()) { return ""; } String rest = toStringRec(list, index + 1); if (rest.length() > 0) { return "(" + list.get(index).toString() + ")" + " " + rest; } else { return "(" + list.get(index).toString() + ")"; } }
This implementation works, but is unwieldy. The underlying operation, traversing the list from one end to another, is a fundamental operation on lists. Java provides us a better way of traversing the list, using the for-each loop.
public static String toString(List<String> list) { String result = ""; for (String obj : list) { result = result + " (" + obj.toString() + ")"; } return result.substring(1); }
We can read this code as “for each item obj in list create a string using the string representation of obj and append it to the result.” The type of obj is the same as that of the contents of the list (hence it is String above). In other words, this construct starts at the beginning of the list, gives us a chance to operate on the element it is currently at, and advances to the next element.
7.5.1.2 Printing the list as before with position
Suppose we wanted to print the list as shown in this test:
@Test public void testToStringPos() { List<String> llist = new LinkedList<String>(); llist.add("I"); llist.add("am"); llist.add("a"); llist.add("teacher"); assertEquals("(0:I) (1:am) (2:a) (3:teacher)", StringListUtils.toStringPos(llist)); }
Thus we want a string that contains not only the contents of the list in sequence, but also the position of each item.
When we attempt to use a for-each loop for this purpose we hit a roadblock: this loop gives us access to the objects in sequence, but not to their positions in the list. What if we could iterate through the list in a different way: using positions rather than actual objects? The List<T> interface provides us with a get method that can return the object given its position. What we want is a way to count through the positions of the list and operate on the object at the current position. A counted for loop allows us to do this:
public static String toStringPos(List<String> list) { String result = ""; for (int index = 0; index < list.size(); index = index + 1) { result = result + " (" + index + ":" + list.get(index).toString() + ")"; } return result.substring(1); }
The counted for loop is useful in other situations too. But it is primarily used when a certain block code must be repeatedly executed, and the number of times it is executed is counted in similar increments after starting from a fixed value.
7.5.2 Arrays
So far we have seen one way in which a list of elements can be created: linked lists. In this representation the list is made of several nodes. Each node keeps one element along with where the remaining part of the list is.
This is not the only way to represent a list. An alternative way is to store all pieces of data next to each other in a single, contiguous chunk. This way of representing a list is called an array. The figure below illustrates the structural difference between a linked list and an array.
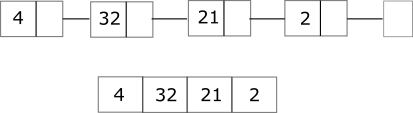
Given a data type T, an array T[] is a fixed-length, mutable sequential list of elements of type T. There are several ways to create arrays in Java.
int[] array = {4,3,1,2}; int[] array2 = new int[4]; String[] array3 = {"I","am","a","good","person"}; String[] array4 = new String[16];
The first example shows how to create an array of integers by explicitly typing the sequence of numbers. This array has a length of 4. The second example shows how to create a “blank” array of 4 integers. Since we did not explicitly give values to it, Java auto-initializes all of them to 0. The third example shows how an array of a non-primitive type (String) can be created similar to example 1. The fourth example shows how to create an array capable of holding 16 String objects. This line just creates the array, not the actual String objects. Java auto-initializes all of them to null. Irrespective of how an array is created, its length cannot change after creating it.
Given an array-type variable, we can determine its length by using its length attribute. An example would be array3.length from the above example, which would have value 5. Notice that length is not a method.
Similar to the positions we have been using, array positions (called indices) begin with 0. For an array of length l, the valid indices are 0..l-1. Given the array array and an index 2, array[2] is the 3rd element in the array (whose value is currently 1 from above). This array-index notation can be used to read or write to that position in the array: array[i] for a valid index i acts like an ordinary variable. Attempting to read from or write to an array using an invalid index throws the ArrayIndexOutOfBoundsException.
Arrays are actually the reason why list indices in Java (and many other programming languages) begin with 0. The technical reason for this has to do with how arrays are stored in memory, and how indexing actually works.
assertEquals(2, array[3]); assertEquals("good", array2[3]); assertEquals(null, array4[0]); array4[0] = "New string"; assertEquals("New string", array4[0]); array[2] = -1; array[1] = array[1] + 5; assertEquals(-1, array[2]); assertEquals(8, array[1]);
Arrays are reference types. Therefore when arrays are directly assigned to each other they merely create aliases.
int[] a = {2,3,1,5}; int[] b = new int[5]; int[] c = a; //creates an alias int[] d = {10,3,1,5}; assertEquals(1, a[2]); assertEquals(0, b[3]); assertEquals(1, c[2]); //identical a[0] = 10; assertEquals(10, a[0]); assertEquals(10, c[0]); //changed! assertEquals(a, d); //identical, but not equal. Fails! assertArrayEquals(a, d); //passes
The correct way to create a copy of an array is to create another array of equal size and then copy the elements one-by-one. The latter step can be done using a counted for loop.
int[] a = {2,3,1,5}; int[] c; c = new int[a.length]; for (int i = 0; i < a.length; i = i + 1) { c[i] = a[i]; } //or use c = Arrays.copyOf(a, a.length); a[0] = 10; assertEquals(10, a[0]); assertEquals(2, c[0]); //did not change
7.5.2.1 Pros and cons of arrays
Arrays are conceptually simple to work with. They are “light-weight,” in that they don’t have methods attached to them like classes. As an array is stored in a single chunk of memory, it has advantages related to speed as compared to linked lists.
Because an array is not a class, we cannot associate operations directly with it as we did with our ListADT interface and ListADTImpl class. Java provides some helpful methods that work with arrays: see the documentation for the Arrays class. They work closer to functional style (“take this array and operate on it”) rather than OO style (“list, operate upon yourself”).
A second drawback is that once an array is created it cannot be resized. But what if we do not know a-priori the number of elements that we wish to store in the array? The only way to “resize” an array is to create a bigger array, copy over all the elements from the old to the new array and then set the old array to be an alias of the new array.
c = new int[some length bigger than a]; for (int i = 0; i < a.length; i = i + 1) { c[i] = a[i]; } a = c; //henceforth this newer, larger array can be referred to as 'a'
Thus if we use arrays and they need to resize we need to do the above operations every time. What if we wanted to leverage the above advantages of arrays, but encapsulate them with their operations and not worry about having to resize? The ArrayList class in Java does just that!
7.5.3 The ArrayList<T> class
True to its name, the ArrayList class is a List (it actually implements the same List interface as the LinkedList class), but is implemented as an array. One can add elements to it without worrying about its length: it resizes itself on-demand. As it implements the List interface all the methods that we used earlier for the LinkedList class can be used with it as well. Since it is a generic class, it can be used only with non-primitive types.
7.6 Higher-order functions using Java’s lists
Earlier we motivated higher-order functions as a useful way to abstract behavior over lists and possibly other recursive union-type data structures. Starting with Java 8, Java lists now (indirectly) support writing many functional programming constructs, including higher order functions.
Most of this support is based on the notion of streams, which is a new and separate representation of sequential data. Streams facilitate writing parallelizable higher-order functions.
Consider a list of books created as follows:
List<Book> bookList = new LinkedList<Book>(); bookList.add(new Book("HP 1", "J.K. Rowling", 1997, 19.99f)); bookList.add(new Book("HP 2", "J.K. Rowling", 1998, 10.99f)); bookList.add(new Book("HP 3", "J.K. Rowling", 1999, 12.99f)); bookList.add(new Book("HP 4", "J.K. Rowling", 2001, 15.99f));
7.6.1 Map: Extracting all authors in a list
What if we wish to construct a new list that contains authors of the above books, in the order of the books themselves? We would have to traverse the above list, access each author and populate another list with it. We could accomplish this with a for loop as follows:
//Objective: extract all the titles List<String> allTitles = new LinkedList<String>(); // Accomplishing this with a for-each loop for (Book b:bookList) { allTitles.add(b.getTitle()); } assertEquals("[HP 1, HP 2, HP 3, HP 4]", allTitles.toString());
Instead we can write a map operation from List<Book> to List<String> using the map method:
//Objective: extract all the titles // Accomplishing this with a map function (List<Book> => List<String>) List<String> allTitles = bookList.stream() .map(b -> b.getTitle()).collect(Collectors.toList()); assertEquals("[HP 1, HP 2, HP 3, HP 4]", allTitles.toString());
Specifically:
bookList.stream() converts the List object into a Stream object. This object supports various higher-order functions.
We invoke the map method of the stream. We pass it a lambda function b->b.getTitle(). Since this is called on a stream containing Book objects, the type of b in the lambda function is inferred automatically. Similarly the return type of getTitle implies the type of the resulting stream.
The method collect is used to go the other way: convert a stream into a Collection object. Specifically we convert it to a list.
7.6.2 Fold: Total price of all books
We can compute the price of all books in the list using a loop as follows:
//find the sum of all prices of the books double totalPrice; // Accomplishing this with a for-each loop with a counter totalPrice = 0; for (Book b:bookList) { totalPrice += b.getPrice(); } assertEquals(59.96, totalPrice, 0.01);
Instead we first write a map operation to convert a List<Book> to a List<Double>, and then a fold/reduce operation on it. Java 8 has several inbuilt fold functions. Since we want to find the sum of prices, we use the inbuilt sum method.
//find the sum of all prices of the books // Accomplishing this with the built-in reduce (fold) sum // (List<Book> => double) double totalPrice = bookList.stream() .mapToDouble(b -> b.getPrice()) .sum(); assertEquals(59.96, totalPrice, 0.01);
We can also write the fold operation explicitly. As explained earlier, a fold operation requires an initial value, and a combine algorithm. We use the reduce method for this, passing it an initial value of 0, and a lambda function (a,b) -> a + b. Once again the types of a and b are inferred automatically by the type of the calling stream object.
//find the sum of all prices of the books // Accomplishing this with a reduce function that explicitly // starts with initial value of 0, and then combines two elements // by adding them double totalPrice = bookList.stream() .mapToDouble(b -> b.getPrice()) .reduce(0, (a, b) -> a + b); assertEquals(59.96, totalPrice, 0.01);
7.6.3 Compound operation: total price of all books published before 2000
Suppose we wish to determine the total price of all books that were published before the year 2000. We can accomplish this with a loop as follows:
//Objective: find the titles of all books written before 2000 double totalPrice = 0; for (Book b:bookList) { if (b.getYear() < 2000) { totalPrice += b.getPrice(); } } assertEquals(43.97, totalPrice, 0.01);
We can accomplish this with a combination of higher-order functions as follows:
We filter the list of books to include only those books that were published before 2000.
We map the filtered list of books into a list of prices.
We fold the list of prices using the sum method above.
// Objective: find the titles of all books written before 2000 // Accomplishing this with a filter (List<Book> => List<Book>) // followed by a map (List<Book> => List<Double>) and then a fold totalPrice = bookList.stream() .filter(b -> b.getYear() < 2000) .mapToDouble(b -> b.getPrice()) .sum(); assertEquals(43.97, totalPrice, 0.01);