Lecture 19: Strategies and Decorators

19.1 Design Problems

An important design goal is scalability. Often we do not know every requirement in a design, but anticipate some future enhancements. If code is designed not only to work correctly with the given requirements but also support adding some future features then the design is protected from variations.

While this is a noble aim, anticipating most or all future changes is infeasible. However different situations of what may come in the future lead to specific designs that aid in preparing the design for the future. We will see two such situations in this lecture.

19.2 Replacing the guts of a class

Let us imagine we wish to create a game of Tic-tac-toe. We may have a version of the game where two human users can play with each other, or have a human player play the computer. In case of the latter, the computer must determine which move to make next. There are several alternatives:

• Scan the board row-wise and play at the first available position

• Choose a random available position

• If a move will result in a win, choose that move

• If the opponent is one move away from a win, block that win

All these alternatives formulate the strategy of a player. Similar to the design above we can create a Player class that implements all necessary operations. We isolate the method to determine the next move, and then implement one subclass for each alternative above.

However subclassing has several drawbacks:

1. A new class is created for every alternative. While this class may not be big because we minimized code duplication we end up creating an entirely new data type just when one part of it changes

2. It is difficult to create a version that combines several alternatives.

The second drawback is even more glaring for the Tic-tac-toe example. Only the first two strategies (choose first available, choose random) are complete, in that they will always result in a position being chosen so long as the game is not complete. The latter strategies are incomplete. A more practical strategy would be to block a win if applicable, otherwise choose a random position. An even better strategy would be to try to win, if not block a win and as a last resort choose a random open position. All of these composite strategies will be subclasses, even though they are partly implemented in other classes.

19.2.1 The Strategy Design Pattern

Recall how we arrived at the subclassing design: we abstracted out the common parts until we isolated the method that is actually different depending on the strategy. In general we can use this technique to isolate the strategy to a single method that must be implemented in different ways. Instead of creating a separate class for each such implementation we express this method as a function object and allow the original class to accept a function object.

We can then create different implementations of this function object, each encapsulating a strategy. In order to create a composite strategy we create an implementation that stores a reference to another strategy. Its implementation would try the incomplete strategy in itself, and if it is not applicable use the other strategy. This allows us to create an arbitrary chain of strategies in general.

19.2.2 Strategies to sort

Several applications need to arrange data in a non-ascending or non-descending order. There are several sorting algorithms that can be used for this purpose. Although the theoretical performance of all these algorithms is known, the practical performance often depends on the actual data. Therefore it may be desirable for certain applications to use and switch between sorting algorithms depending on some criteria. We can implement this ability to switch using strategies.

We start by defining the basic strategy as an interface.

We then define our proof-of-concept class that manages data. It accepts a strategy during creation to use for sorting.

We now define a simple strategy using the traditional insertion sort algorithm.

Similarly we can define a sorting strategy using the traditional top-down recursive merge sort algorithm.

We can use these strategies to sort data with our Arranger object:

19.2.3 A hybrid sorting algorithm

Many practically used sorting algorithms are hybrids of existing algorithms. For example, it has been observed that insertion sort, although quadratic in time, is more efficient for smaller arrays than the merge sort algorithm. We can exploit this by implementing a hybrid sorting algorithm: we use traditional merge sort, and when the sub-array is small enough we can resort to insertion sort instead.

Using the strategy pattern makes it easier to define such a hybrid sorting algorithm by composing existing strategies. The strategy pattern guarantees that such a composite strategy can be plugged in to any client that accepts such a strategy.

19.2.4 When is the Strategy pattern applicable?

The Strategy pattern is applicable when an operation can be implemented in several ways by replacing how a part of it is implemented. It is especially helpful if we need to compose an algorithm using other algorithms that solve the same problem but in a simpler or restrictive way. In essence using the strategy pattern allows us to change the “guts” of how a class is implemented. The advantage of using a strategy pattern over subclassing is that it allows us to change dynamically the strategy used by an object (i.e. we can create a tic-tac-toe player object and dynamically change the strategy used by it without having to create new player objects every time).

A useful analogy to a strategy is creating a Halloween exhibit. We’d like all our exhibits to look like pumpkins but instead have lights or other props inside it. So we carve the guts out of the pumpkin and cut open a lid, so that we can insert anything into the pumpkin. Similarly a strategy pattern makes it easy to carve out and replace the guts of an algorithm.

19.3 Adding a new operation to an object

A GUI library typically has widgets to draw certain UI elements. For example most libraries have a label to display static text, a text area that is used to enter several lines of text, a panel that acts like a rectangular placeholder to contain other elements, etc.

We need to add the ability to scroll each of them. This is useful if the size of the widget is greater than the screen-space given to it. Scrollbars may or may not be needed depending on whether this size disparity exists or not. We can create scrollable versions of these widgets. Because we want to retain the original classes, we create subclasses that implement these extra operations.

Similar to scrollbars, we wish to also add borders around any rectangular widget. We face the similar constraint, in that we need bordered and borderless versions of these widgets. We follow the same design as before: subclass the original widgets and implement extra operations.

This way of designing is not scalable. In order to add one new, optional feature to 3 types of objects we created 3 new classes, and then 3 new classes for each new feature after that. Moreover we have lots of code duplication. In the above design we are “reimplementing” the scrolling and border features across all widgets.

But there is a bigger problem with this design. What if we wanted to create a “scrollable bordered” widget? This represents a combination of new features. This would create 3 new classes that combine the two new features. If we add one more new feature X it would create a total of 12 new classes: 3 classes for a widget with X, 3 classes for a widget with X and Scrollable, 3 classes for a widget with X and Bordered and 3 classes for a widget with X, Scrollable and Bordered! Clearly this design cannot be sustained as more features are inserted into existing classes.

19.3.1 Adding features to objects, not classes

The above design is effectively adding new methods into classes without changing them. Consider this alternative design:

Instead of subclassing the scrollable uses composition to reuse the widget. Thus the scrollable “contains” the widget to be scrolled. The critical aspect of this design is that the scrollable is a widget, so it can be used wherever a normal widget applies. The extra functionality is implemented only once, in the Scrollable class. Compare the Scrollable keeping a reference to a widget to the design of the strategy pattern above. Such a link allowed the strategy to be composed of other strategies. We can use a similar idea to create bordered widgets.

This is the decorator design pattern. This design has the following aspects:

• A decorator allows us to “attach” and “detach” new methods to an object dynamically (i.e. without having to create a separate object and without having to change its source code).

• A decorator allows us to combine several features in a scalable manner.

• All routine operations can be delegated directly from the decorator to what it contains (this makes a scrollable label still a label).

19.3.2 When is the Decorator pattern applicable?

A decorator is applicable when new operations need to be added to an object in a dynamic manner (i.e. at runtime). Decorators are especially useful if these new features treat the underlying object as a black-box. For example scrolling and bordering only treat a widget as a rectangular area, irrespective of what they contain/show. Think of a decorator as “gift-wrapping” the original object.

19.3.3 Decorators to enhance existing operations

The above introduction to decorators is a bit unusual. Decorators are typically used to enhance existing operations. In this traditional sense, objects can be decorated “transparently”. That is, an object is used in the same way as its decorated self. This use of decorators is seen when an existing operation of an object is restricted or enhanced in a certain way.

A practical example of traditional decorators are the stream classes in Java (I/O streams, not the Stream API). In Lecture 12: Abstracting a controller we introduced the OutputStream class. This abstract class is the superclass of all classes that represent an output stream of bytes. An output stream accepts bytes and writes them to a data sink. For example the FileOutputStream and ByteArrayOutputStream classes write bytes to files and byte arrays respectively.

Depending on the nature of the specific data source, it may not be advisable to write a single byte of data to it each time a byte is sent to the output stream (for example, writing data one byte at a time to a file on disk is very inefficient). A good strategy is to “collect” bytes to a temporary buffer in main memory, and periodically empty the buffer to disk. This strategy is called buffering, and is very common. However output streams have no such in-built capability. Thus, to add this capability we must “enhance” the write operation offered by an output stream.

The FilteredOutputStream class defines a general-purpose decorator for OutputStream objects. It stores an OutputStream delegate, and defines/overrides all the OutputStream methods to pass on the data to the underlying delegate. The BufferedOutputStream class subclasses the FilteredOutputStream and implements the buffering mechanism. The following code snippet shows an example usage.

We can define our own custom-decorators on output streams as well.

19.3.4 Writing characters in lower case

Let us assume our program writes characters to a file. We use a PrintStream to decorate the FileOutputStream object. This gives us the buffering mechanism, and the ability to write entire strings at a time.

The above program writes the input string verbatim to the file.

What if we wanted to write messages to the file, but in lower case? We could manually convert each string to lower case before writing it, or we can decorate the output stream with this ability. To do this, we will create a new output stream.

We now override the write method. We convert the character to be written to lower case before sending it to the delegate.

We can now use this to decorate our PrintStream object from above:

Note that the extra feature (writing only lower-case to the file) did not change our writing code at all, except creating the decorated stream. The above code writes the string “i love program design paradigms. this is a great course!” to the file.

19.3.5 Simple encryption as decorators

We can use this to implement more drastic transformations on the bytes before writing them to a data source. For example, we can encrypt bytes using many encryption schemes.

As a simple proof of concept, we implement a one-character shift cipher. A shift cipher on an alphabet of characters works by “shifting” each character by a fixed number of places in the alphabetic sequence. For example, a simple shift-by-1 cipher would convert ‘a’ to ‘b’, ‘b’ to ‘c’, and so on, finally converting ‘z’ to ‘a’. The corresponding deciphering algorithm would shift-by-1 in reverse.

We implement this by defining another decorator.

We can then use this to decorate our earlier stream as follows:

Again, the encryption is transparent to the code, other than creating the decorated stream. The above code writes the string “J mpwf Qsphsbn Eftjho Qbsbejhnt. UIJT JT B HSFBU DPVSTF!” to the file.

19.3.6 Dynamic Decoration

One of the main features of a decorator is that objects can be decorated at run time. Thus, the same object can be wrapped and unwrapped in decorators dynamically. For example, we can “add” and “remove” lower-casing and shift-ciphering capabilities while writing to the same file.

The above code writes the same input message four times to the file in different formats: the original message, the original message converted to lower case, the original message encrypted with a shift cipher, and finally the original message first converted to lower case and then encrypted with a shift cipher. The original output stream was not closed as decorators were added, nested and removed to it.

19.4 Decorators vs strategies

How do decorators compare to strategies? The following visual shows how one can start from a single object and then enhance it using both.

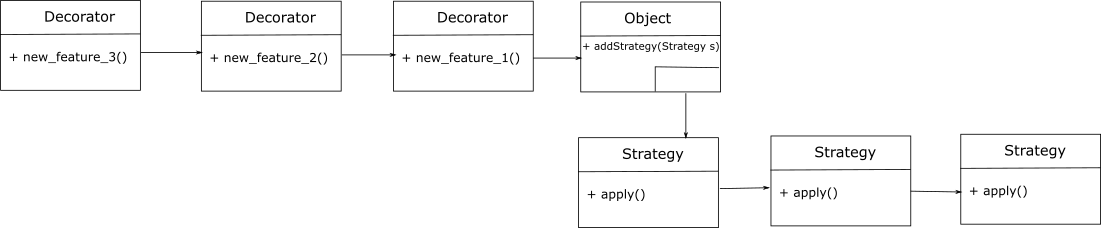
To add a new feature to the object while still supporting its interface, use a decorator. To change the way the object internally works, carve out the strategic part and encapsulate in a strategy. Both decorators and strategies can be composed, allowing us to add several new features and create composite strategies.