Lecture 5: Union Data types

5.1 Introduction

Often we encounter data that can take one of several forms. There are some things that are common to all forms, while others are unique in each form. This is a union data type. We encountered a union type in Lecture 1: The Essence of Objects in the form of various kinds of publications. There are many examples of union types: chess pieces, geometric shapes, types of employees in a company, etc.

Much like the publications example, the design of union types typically takes one of two forms (exemplified in Lecture 1: The Essence of Objects):

• Non-OO: Create several data types, one for each unique form. Write operations as external functions that operate on union-type data. The functions may query the type of data passed to it, and operate accordingly. This is a common design in functional languages, but is sometimes useful in procedural languages as well.

• OO: Consolidate all common operations in an interface, then implement each unique form of data as an implementation of this interface. This is a common design in object-oriented languages.

A subtle difference between the design process of union types and the design process we followed in Lecture 3 and Lecture 4 is that with union types, we know in advance what types must be represented (we may add more types in the future). This means we can often anticipate abstraction and design for it upfront. The remainder of this lecture explores such a design process on a common example of union types: shapes.

5.2 Shapes

5.2.1 Problem

We are building an application that allows an interior designer to draw 2D floor plans of houses. This application allows a user to draw various kinds of 2D shapes on the screen. Common shapes are circles, rectangles, squares, etc. Being on the screen, each shape has a reference point (e.g. the center of the circle, the lower-left corner of a rectangle, etc.). It is useful to be able to compute various properties of a shape, such as its area, perimeter, distance from a global reference point, etc. Shapes are commonly resized as part of the drawing. Shapes also need to be compared to each other based on area.

5.2.2 Interface Design

We begin by distilling from the above description a list of operations that all shapes ought to offer. They are:

• A method to compute and return the area of the shape.

• A method to compute and return the perimeter of the shape.

• A method to compute and return the distance of this shape (i.e. its reference position) from the origin. We treat the origin as the global reference point.

• A method that compares two shapes based on their area and returns the result.

• A method that creates a "resized" version of this shape.

Most of the above operations seem "observational," i.e. they compute and return a value based on the attributes of the shape. The last operation "changes" a shape. We can characterize this operation in two ways: "change this shape" or "create a new, changed version of this shape". We adopt the latter definition, as it does not mutate the object.

5.2.2.1 Why avoid mutation?

Whenever there is a choice between immutable and mutable objects, choose the former. It avoids many pitfalls and errors. There are situations where the benefits of mutation exceed its pitfalls. We will see such cases in future lectures.

The notion of not allowing any side effects is sometimes referred to as "purity" or "pure programming." Functional programming languages embrace this concept by default, but it can be deliberately adopted in many other languages.

A mutation is when an attribute of an existing object is changed after it has been created. This change is done most often through one of the methods of that object. Such methods record the effect of their operation within the state of the object, rather than or in addition to returning it to their caller. Often a method is written that mutates the state in a way that is not obvious to its caller. This causes side effects (intended or unintended) on the object, and has the potential to cause hard-to-find bugs in code. Making an object immutable is a reliable way to avoid this problem. In fact, one of the hallmarks of most functional languages is that they do not allow mutation. Every function can be thought of as producing an output from some input data that does not change.

5.2.3 The interface

We put the above methods in a Shape interface.

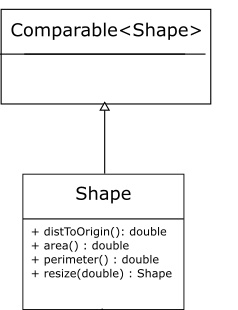
Do Now!

Pay attention to the types used in the interface, and argue why they are a good choice.

5.2.4 Shape attributes

What attributes do our shapes have?

• They all have a reference point, represented by x and y coordinates. Each shape has its own context of this reference point (e.g. it is the center for a circle, but a corner for the rectangle), but that does not change how it is represented.

• A circle has a radius, which is unique to it.

• A rectangle has a width and height, which are unique to it.

• A square has a side.

Inheritance represents a "is-a" relationship between two classes. Programmatically inheritance allows a (derived) class to inherit all attributes and methods of another (base) class. However the main reason to use inheritance is that it accurately represents the relationship between what the two classes represent. Thus, using inheritance (or not) is a design decision.

We also observe that a square is a special type of rectangle (with width and height equal to each other). We can represent this relationship between shapes using inheritance between their classes. Specifically, our Square class extends the Rectangle class.

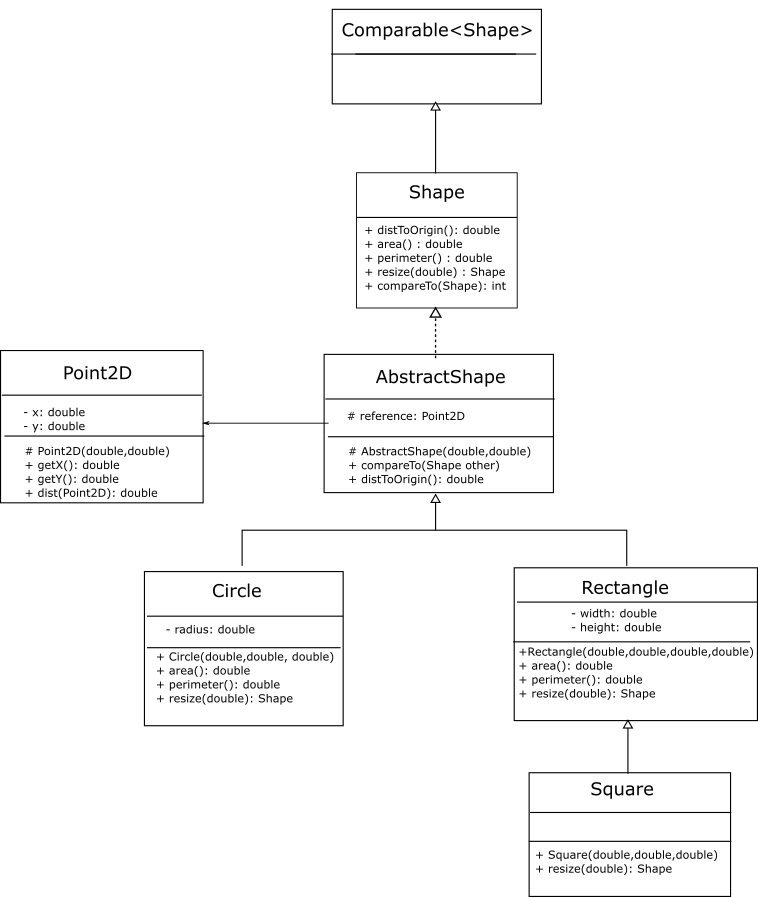
Our preliminary design can be expressed as:

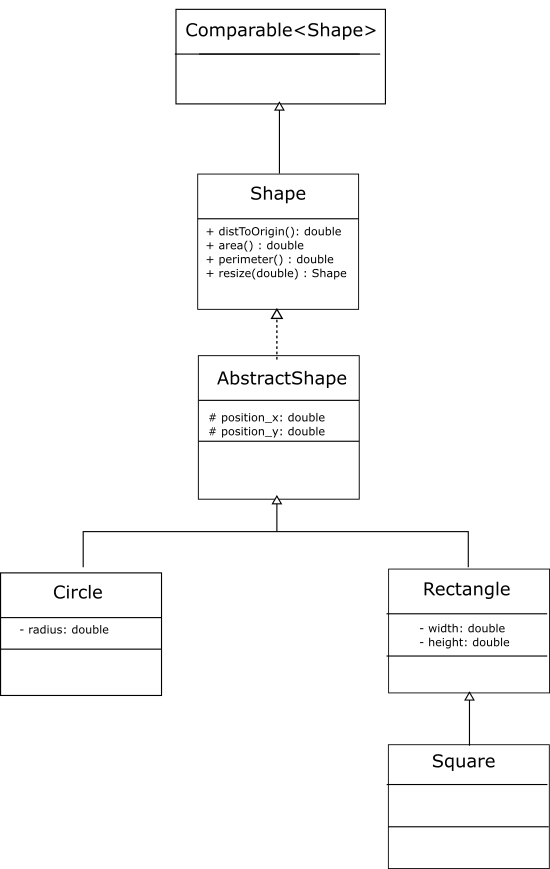
As we may need to access reference positions in the concrete classes, we make them protected in the AbstractShape class.

5.2.5 Constructors

A direct way to instantiate various shapes would be to provide all their relevant data. For the circle this means the reference position and radius, for the rectangle it is the reference position, width, and height, whereas for the square it is the reference position and length of the side.

It may seem odd that a (abstract) class that, by its very definition cannot be instantiated, has a constructor. In this case think of its constructor as simply a one-stop method to initialize any common fields that this class has. Often this constructor is marked as protected to further underscore its status as an "internal" method.

We have placed the fields for the reference positions in the AbstractShape class. Therefore it makes sense to initialize these fields in that class as well. Accordingly, we can write a constructor in the AbstractShape class that takes the reference position as arguments and initializes its fields. Because this constructor will only be called from its subclasses, we make it protected.

The constructors for the concrete classes now call the constructor of their base class (AbstractShape) and pass it the arguments for the reference position. In Java we can call the constructor of the base class as super(...);. This must be the first line in the constructor of the derived class.

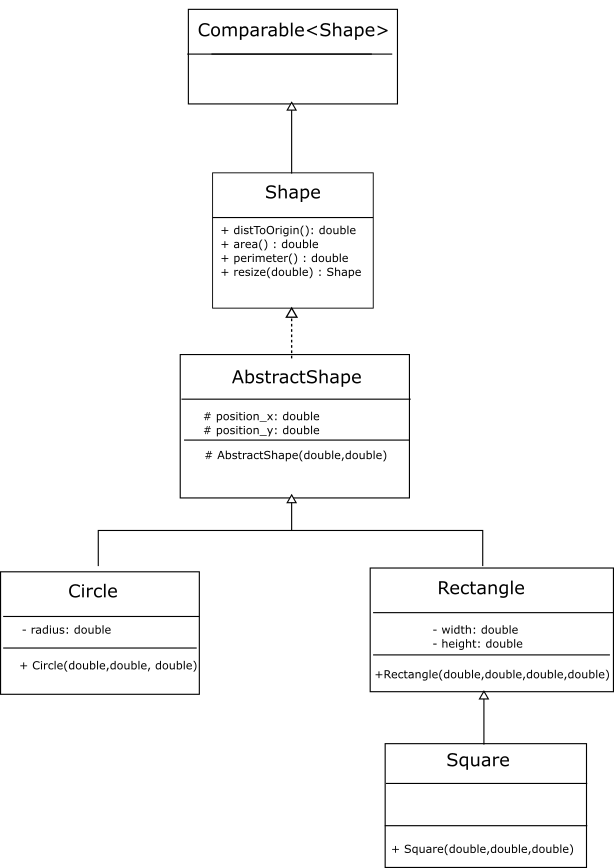
5.2.6 Methods: area, perimeter, resize and comparison

Some of the methods are fairly straightforward. Each shape has a different way of computing its area and perimeter, so these methods have to be implemented in their respective classes. Taking advantage of inheritance, the Square class would simply reuse these methods from the Rectangle class.

Each shape’s resize method creates and returns a resized version of itself. Therefore each class can implement its own resize method. In this case the Square class must implement this method as it must return a Square object.

Our method of comparing two shapes uses their area. As we did in Lecture 3 we use the Comparable interface to provide an "official" way of comparing two shapes. As all shapes have an area method we can implement this method fully in the AbstractShape class. Our design evolves to:

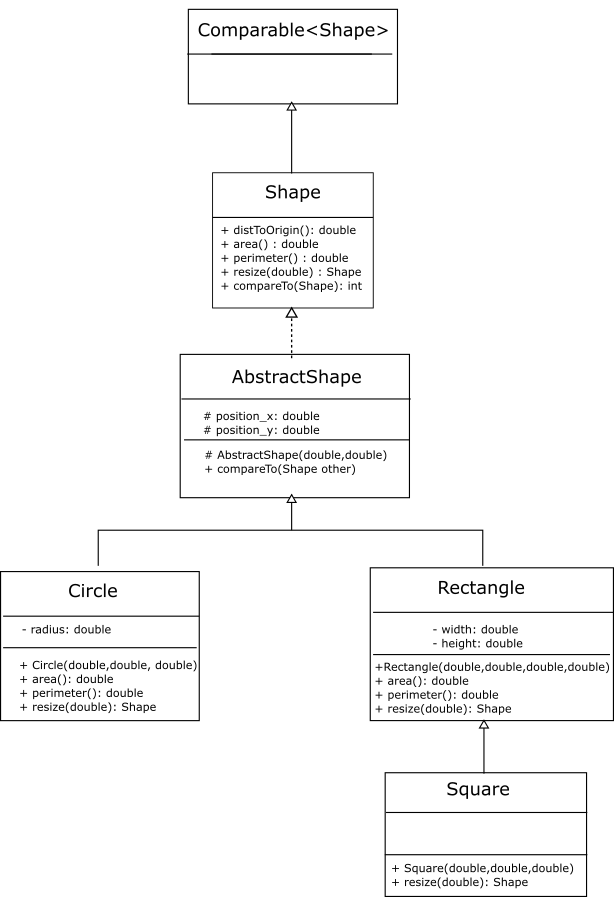
5.2.7 The distToOrigin method

The distToOrigin method implements the above formula but for \(c=d=0\). Since the reference position of each shape is part of the AbstractShape class it makes sense to implement the distToOrigin method there.

However we observe that the above arithmetic is relevant to 2D points, and not shapes per se. It can be useful in other (hitherto unknown) contexts as well, and putting it in the AbstractShape class will make its reuse more difficult (one will have to use the shape classes just to get the Euclidean distance implementatoni). This leads to the possibility of refactoring out and encapsulating the "reference point" part of a shape into a new class that represents a 2D point.

Given our current design, how can we refactor it for this?

• Create a Point2D class. Add attributes x and y and a constructor that takes the x and y coordinates of a point.

• Implement observer methods (getters) for its x and y coordinates, so that the shapes may query their reference positions as before.

• Implement a method to compute the Euclidean distance between two Point2D objects. For example, its signature may be

  public double dist(Point2D other)

• In AbstractShape replace the two protected attributes position_x and position_y with a single protected attribute reference of type Point2D.

• Change the implementation of the constructor of the AbstractShape to call the Point2D constructor with the position passed to it.

Note that the changes to the AbstractShape class do not affect any of its subclasses, so no other code needs to change.

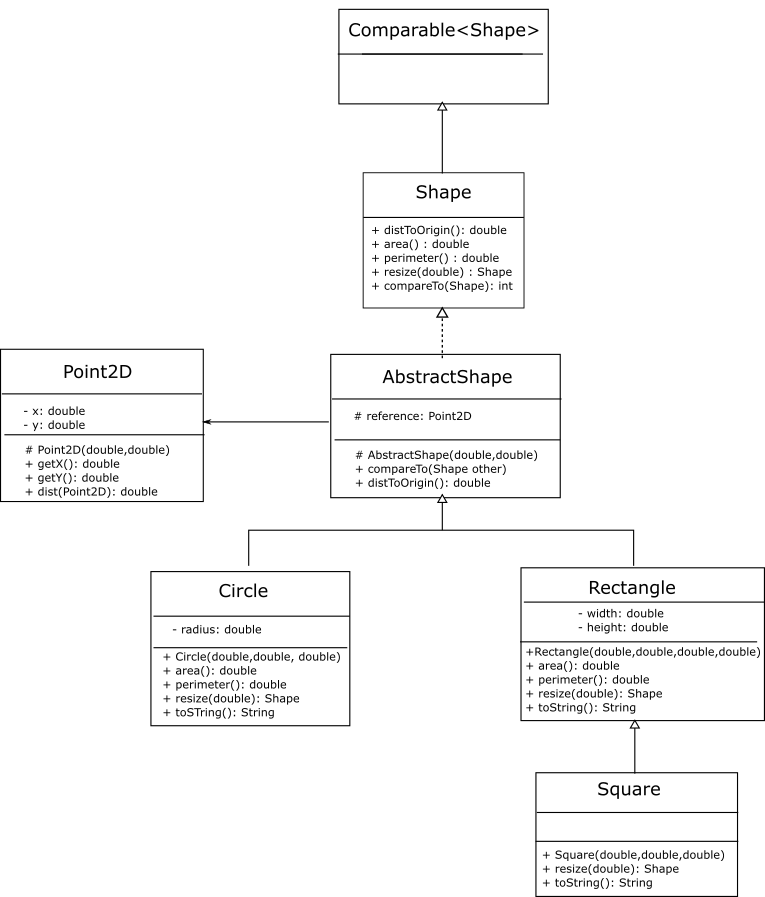
We can now put the distToOrigin implementation in the AbstractShape class. It will simply use the dist method of the Point2D class to compute the distance between its reference position and the point (0,0).

5.2.8 The toString method

How do we test these classes? When we instantiate the shape objects we must verify that they have been created correctly. We could test this indirectly by using its observer methods (area and perimeter), but we do not have observer (i.e. getter) methods for each attribute specifically. We can add such methods, but there are two problems:

• As a design rule, one must not add a method to a class or interface unless there is at least one situation where it will be used. Being able to test an implementation is, by itself, not a justification (these methods will not serve any relevant purpose for the client).

• As the attributes of each shape are different, we would need to write different observer methods for each shape. This would mean that each concrete shape, in addition to implementing methods from the Shape interface, will now have methods unique to itself. This breaks our abstraction (we will no longer be able to use Shape-type variables to refer to objects, as we will not be able to call these unique methods using them).

Every Java class has a default public String toString() method because it extends the Object class. The default implementation of this method prints some generic (and often useless) information about the object. Therefore it needs to be overridden in most cases.

It would be helpful to have an operation that converts a Shape object into a string representation. If the string representation contains information about the object, it can be used in a test. It can also be used in other situations (e.g. printing an object in a human-readable form). This object-to-string conversion is important and general enough for Java to provide such a method by default to all its classes: public String toString().

Beyond the specification that it returns a String representation, there are no other rules about its format. We can therefore decide on any formatted string that fulfills our purpose, so long as we document it clearly. For example, we decide that the toString() method of the Circle class should return a string formatted as "Circle: center (3.000,4.000) radius 5.000". For our purposes of testing, this string contains all attributes and thus we can use it to verify the correctness of an object’s attributes. We would need to decide the format of this string for each specific shape and implement it in the corresponding class.

Note that implementing the toString method in all our shape classes does not change their interface. This is because Java already provided them with a (default) toString method. Therefore even if this method is implemented in the shape classes as an afterthought, it has no effect on any existing client code.

5.3 Implementation

Our design of these classes is now complete, and we can write the implementation.

Note that most of our discussion above happened without actually writing any code. We started with a shell design: Shape interface, AbstractShape, Circle, Rectangle and Square classes. We then thought about each method’s implementation and distributed it among these four classes. We restricted our discussion to strictly "what" the method does and if one could implement the method in terms of other known methods. Most of our issues were addressed during the design, so that implementation (i.e. writing code) becomes a straightforward activity.

When the codebase for an application becomes larger and more complex, it becomes more difficult to examine and reason about design choices, refactor the design and the code. It is often easier to examine design choices and unearth potential problems by looking at design representations (such as class diagrams and interfaces), rather than directly reading code whose understandability may be subjective or even questionable. This may be even more helpful when one must understand and modify code written by somebody else: reverse-engineering the design from an implementation helps in such cases.

5.4 Equality

We would also like to be able to answer the question "is shape A the same as shape B?" Although we have briefly encountered this issue in earlier lectures (see Lecture 3 and Lecture 4), let us examine this issue in more general terms before we implement it for shapes.

5.4.1 The general notion of equality

It is obvious that our definition of equality for any kind of data should have these three properties. We must keep this in mind when we define what it means for two objects to be "equal" to each other.

Java provides two ways to check equality of two pieces of data. One way is to use the == operator (i.e. if (a==b) {...}). In case of primitive types, this operation works correctly and as expected. However since reference types store memory addresses, the == operator effectively determines if both are "literally the same object." Thus == determines shallow, intensional and nominal equality.

The second way (available only for objects) is to use the equals(..) method. The default implementation of this method compares references (and hence is equivalent to using the == operator). However unlike the == operator, we can redefine the equals method for our classes. We did precisely this for the Duration classes in Lecture 3 and Lecture 4. Thus, although the default equals method determines shallow, intensional and nominal equality, it is possible to override it to determine deep, extensional or structural equality as per the context.

Let us review our design template for writing an equals methods (See Comparison and other methods):

5.4.2 Equality for shapes

Our shape classes will be used in the context of a drawing application. To match our typical use-cases, our definition of sameness is as follows: "shape A is the same as shape B, if they are both of the same type and they coincide perfectly with each other when drawn on the screen." The latter part of the definition is clear (and dependent on the dimensions), but the former part implies that a "square" is considered a different shape from a "rectangle" with the same reference position and identical width and height.

Do Now!

Is our definition of shape equality reflexive, symmetrical and transitive?

We apply the above design template to the Circle class as follows:

Similarly we implement the equals methods for Rectangle and Square. Remember that we need to implement it separately for the Square class because our definition of equality says that a square is different from a rectangle of identical dimensions and reference (i.e. the type of shape matters).

Our equals method not being symmetric is not a case of bad luck: whether two objects are equal to each other depends on the order in which you compare them when you write code! This is a classic example of a hard-to-find bug: it works correctly some times but not others.

returns true! This is because a Square extends Rectangle, so a Square object is an instance of a Rectangle object. Thus our implementation violates the symmetry property of equality.

If we trace the origins of this problem, they are in the fact that the parameter of equals method is of type Object, necessitating the instanceof that creates this problem.

5.4.3 Equality of shapes: Take Two

Let us take a step back. How would we write a method that only compares a circle with another circle? We can do this by writing a method

in the Circle class. How can we generalize this to compare any shape to a circle? We can do this by writing the equalsCircle method with the above signature in all the shape classes. Its implementation in all the shape classes except for the Circle class would simply return false, as those shapes are fundamentally not circles.

How do we force all shapes to have a method boolean equalsCircle(Circle other)? We could add it to the Shape interface. But doing so clutters the interface as it will have a lot of these shape-to-shape comparisons that reveal specific implementations (violates the Dependency Inversion Principle, see note in Lecture 3). Also doing so exposes this method to anybody using Shape objects, whereas this seems more to be a matter internal to shapes (a client should be able to simply call one method for equality, instead of choosing from several methods depending on the pair of shapes it wishes to compare). So we add it to the AbstractShape class and make it protected.

Since most child classes will have this method simply return false, we can put this default implementation here.

By default the equalsCircle method of all shapes returns false. We override this method in the Circle class so that it compares two circles (this and other) more meaningfully.

Thus our shape classes now have a way of testing equality of any shape with a circle. We can write similar methods to compare any shape with a rectangle and a square.

This solution will allow us to compare any shape to any other shape.

Now let us attempt to write the equals method in the Circle class.

We know that this is a Circle object (because this method is in the Circle class), but we don’t know the type of the object o. If we knew that it was of type AbstractShape we can call its equalsCircle method and pass this to it (why equalsCircle? Because we know one of the objects is a circle, so this is the only comparison that makes sense).

Depending on what kind of an object other really is, the appropriate method will be called (if it is a circle, the sameCircle in the Circle class will be called that will meaningfully compare the two circles, else the default will be called which will return false). Once again, this is due to dynamic dispatch (see Dynamic dispatch).

Similarly we can implement the equals method for the Rectangle and Square classes, replacing equalsCircle with equalsRectangle and equalsSquare respectively.

goes to the equals method of the Rectangle class, which in turn calls the sameRectangle method on s1. This returns false (as it should). Thus the symmetry property is now obeyed.

5.4.4 Double dispatch

The above implementation may appear a bit convoluted, so let us revisit its design. Let shape1 and shape2 be any Shape objects. When we attempt to test for equality, we will either call

The appropriate equals method will be called depending on the type of the calling object (this is dynamic dispatch). Once inside the equals method, it calls the appropriate equalsXXX method depending on which class it is in. It uses the second shape as the calling object for this (after ensuring that is an AbstractShape, i.e. such a method exists). The equalsXXX in turn has several implementations (the default one in AbstractShape, and overridden ones). Once again, dynamic dispatch is used to determine which implementation of the equalsXXX method to call. In summary, two dynamic dispatches are being used to get to the appropriate shape-pair-specific method of checking equality. This is called double dispatch.

The advantage of using double dispatch is the same as that of using dynamic dispatch. Without double dispatch, our equals method would have taken the form:

In general, we will have to check for individual types, starting from the "most specific" subclasses (Square so far) and making our way up the inheritance hierarchy. Imagine the code changes if we introduce new shapes after writing all these methods!

can be "funnelled" to the correct method by checking the types of objects for both shape1 and shape2 (we write a default equals method that return false and then write a equals(Circle) in the Circle class, equals(Rectangle) in the Rectangle class, etc. Then the "correct" equals method will be called by checking the type of both calling object and argument). Java does not do this, so we must resort to writing several equalsXXX methods. Functional programming languages typically implement "true" double dispatch, so this implementation is simpler in them. However the merits of using double dispatch over checking for specific types still holds in Java (even if a bit clunky).

5.4.5 New shapes?

What if we create a new type of shape, say a triangle?

One option is to make it part of this hierarchy by saying

to the AbstractShape class that returns false, and then overriding it meaningfully in the Triangle class. Compare these changes to those required in the no-double-dispatch code above.

While having to edit AbstractShape is undesirable, it is unavoidable. Note that we created the abstract class purely for better design. A user of these shape classes needs to work only with the Shape interface and concrete shape classes, never AbstractShape. Thus while editing the AbstractShape is not ideal it does not have an impact on the user code (and thus it qualifies as internal code refactoring).

The second option is to create this class separate from this hierarchy by saying

Then we can write its equals method independently. By not putting it as part of this hierarchy, we have implicitly stated that none of the AbstractShape-type objects can be equal to this object.