12 Homework 14
This assignment is due Monday, 4/14 by MIDNIGHT
This HW has TWO parts – Part A, which is autograded, and Part B, which is manually graded. They have SEPARATE submissions on gradescope.
Please submit the respective halfs to HW14A and HW14B on Gradescope.
What to Download:
This is the starter file for the A part of the HW. For the B part, submit either a single file, multiple files, or a zip file, with your solution.
12.1 Part A: Performance
IMPORTANT:
Since LSL does some things that make performance testing a little more difficult, for this assignment, we are using Racket instead. Not only is Racket a lot faster, it has a lot more "normal" performance characteristics.
We are using a library, lsl/performance, provided by LSL, to measure & graph the performance of functions.
Technically, since we are measuring average performance, we are measuring big-θ, which is average case complexity, rather than big-O, which is worst case complexity, but for the problems we are looking at, which do not involve randomization, the distinction shouldn’t matter.
In each problem, you’re asked to move the function down a complexity class. i.e., in the list below, if you measure the function to perform at, e.g., O(n^2) (quadratic), then your task in to change it so that the code behaves as O(n) (i.e., linear), but O(1) (constant) would be fine as well. One important note: if you only test the functions on very small inputs, they may look constant when they are not. Since every problem can be moved down, none of them start out constant, but beware of doing inadequate measurement.
O(1) < O(n) < O(n^2) < O(2^n)
Note that there are many other complexities that fit it between these (e.g., O(n*log(n))), but distinguishing them from the others via a small enough number of samples might be hard, so we are simplifying (and, e.g., we’d consider O(n*log(n)) to look linear, as it often essentially behaves).
For reference when trying to understand the graphs produced by visualize, here are examples of simple graphs for each of the complexities:
(require lsl/performance)
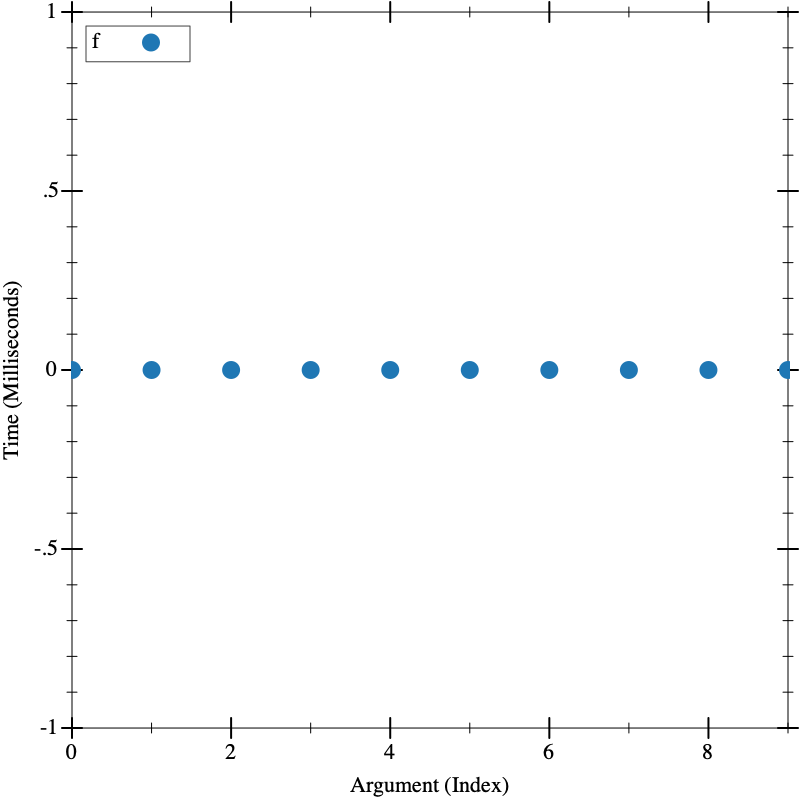
O(1)
(define (f _) 1) (visualize (build-list 10 (lambda (n) (* n 1000))) f)
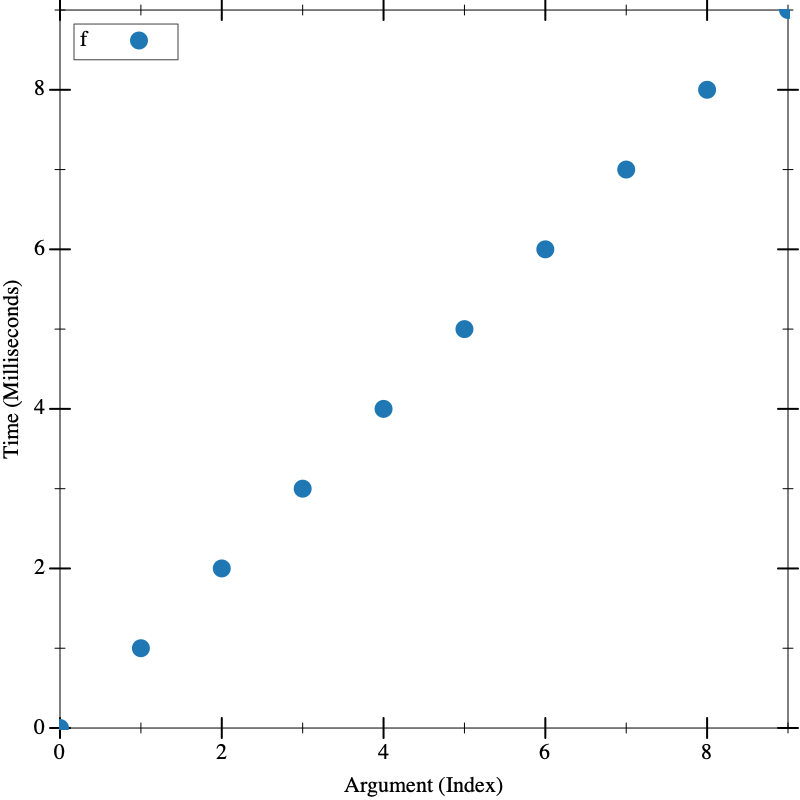
O(n)
(define (f n) (if (zero? n) 1 (f (sub1 n)))) (visualize (build-list 10 (lambda (n) (* n 700000))) f)
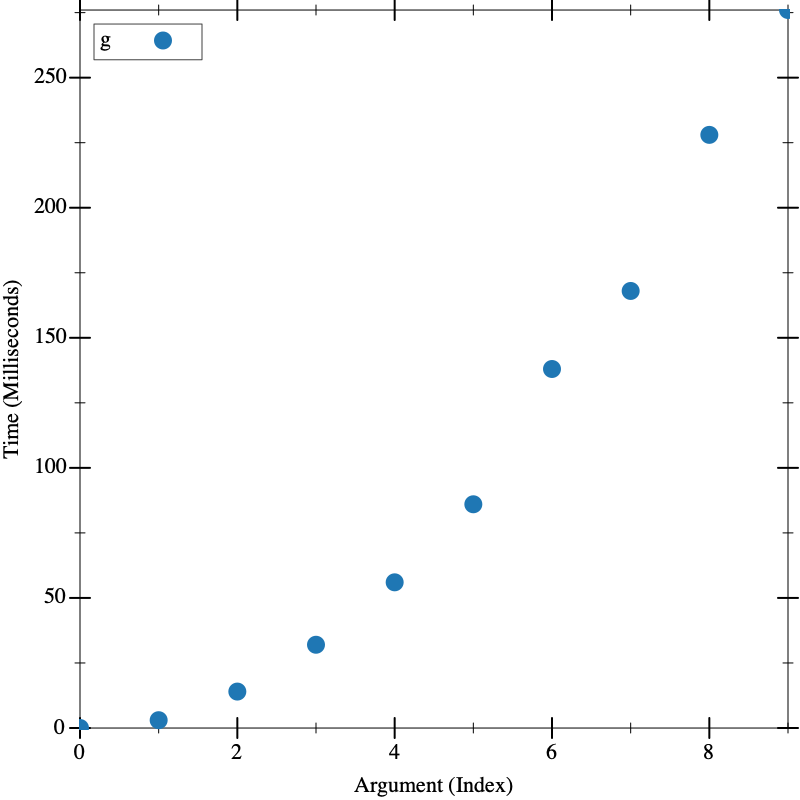
O(n^2)
(define (g n) (local ((define (f n) (if (zero? n) #t (f (sub1 n)))) (define (gl k) (if (zero? k) #t (and (f n) (gl (sub1 k)))))) (gl n))) (visualize (build-list 10 (lambda (n) (* n 2000))) g)
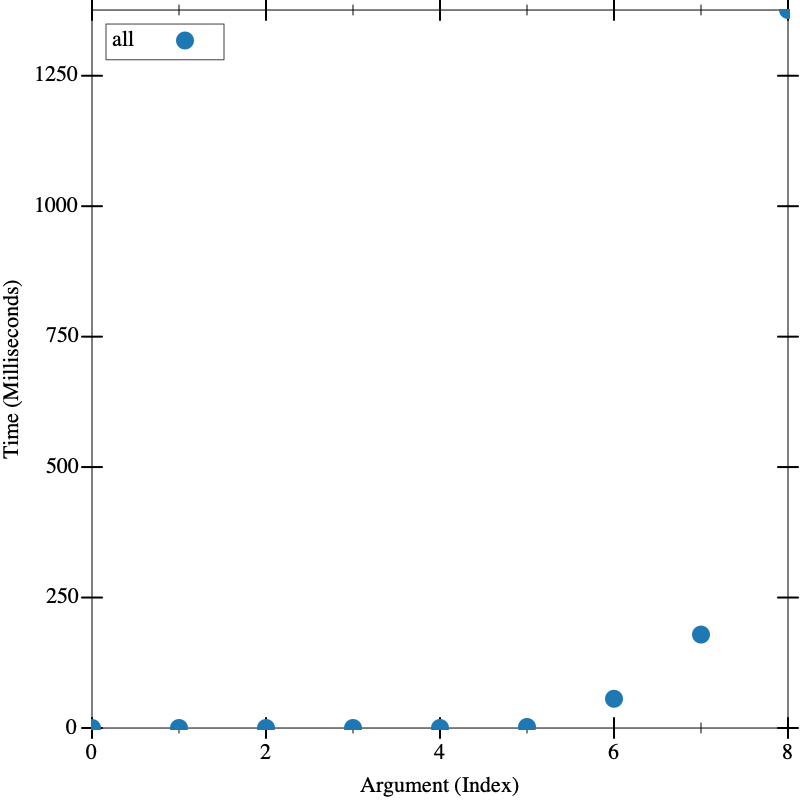
O(2^n)
(define (all n) (local ((define (all-local n) (cond [(zero? n) '(())] [else (let ([xs (all-local (sub1 n))]) (append (map (λ (x) (cons 1 x)) xs) (map (λ (x) (cons 0 x)) xs)))]))) (map reverse (all-local n)))) ; Going up by 3, but gets so fast towards end, showing intermediates (visualize '(0 3 6 9 12 15 18 19 20) all)
12.2 Problem A:1
Consider the following function. Investigate it using visualize, figuring out appropriate inputs to pass to it to discover the time complexity (one of the four above), and then modify the code to shift it to a lower complexity class.
| (define (list-reverse l) |
| (cond [(empty? l) empty] |
| [(cons? l) (append (list-reverse (rest l)) (list (first l)))])) |
NOTE: you may not use the built-in reverse function.
12.3 Problem A:2
Consider the following function. Investigate it using visualize, figuring out appropriate inputs to pass to it to discover the time complexity (one of the four above), and then modify the code to shift it to a lower complexity class.
| (define (fib n) |
| (cond [(<= n 1) 1] |
| [else (+ (fib (- n 1)) (fib (- n 2)))])) |
12.4 Part B: Revisiting Your PBT Library Choice
In this part of the assignment, you will return the the Property Based Testing library you identified and wrote a memo about in Homework 10. Specifically, we want you to solve several problems using it.
You should submit all the code for the below problems – either in a single file, in multiple files, or a zip file with all necessary files.
If you have multiple files, please include a README file that is text that explains how to run your code.
12.5 Problem B:1
Test out your property-based testing library by implementing the following functionality in your language, writing property-based tests, and running them:
Show that sorting a collection (array, list, etc) does not change the size of the collection.
Write code that adds an element to a collection (array, list, etc), if it doesn’t already exist in it, and show that it does not decrease the size of the collection.
12.6 Problem B:2
In this problem, we want you to use an existing JSON serialization/deserialization library (if your language does not have one, you can of course implement it, but that’s not our intention).
First, you need to define a data structure (in your programming language) that represents a map from student ids (as strings) to structures representing students (with a name, list of interests, and address). This data structure is part of a hypothetical application for matching students with people who live near them and have similar interests, the rest of the application will not be implemented!
Now, you should write code that turns that data structure into JSON (using whatever functionality is available in your language’s JSON library), and separate code that does the reverse. This would be used to either store the data, or send it over the network.
Now, write property-based tests that show that for random examples of your data structure, the serialization and deserialization functions are inverses of each other; i.e., that deserialize(serialize(x)) = x for all x.
12.7 Problem B:3
In this problem, first define a native data type for a color, which should be able to represent colors in the following three ways:
Named colors (Red, Green, Blue, etc: how many is up to you, but a finite number)
RGB colors (three numbers, 0 to 255, that represent the amount of Red, Green, or Blue in the color)
CMYK (four numbers, 0 to 255, that represent how much Cyan, Magenta, Yellow, and Black, in the color)
Now, write code that turns your color into a "packed" representation as an array (or list) of numbers. You are welcome to choose any representation as you like, but we’d suggest using the first number as a "tag" that indicates which possibility you are in.
Next, write code that takes a "packed" representation as an array (or list) of numbers, and convert it back into the native color data structure.
Finally, write property based tests that show that for random examples of your color, the "unpacking" and "packing" functions are inverses of each other; i.e., that unpack(pack(x)) = x for all x. You should also show that for any array (or list) of numbers, the "unpacking" function either gives a sensible error, or returns a color that, when "packed", gives the same array (or list) of numbers.