Lecture 7: Using LSL III

1 Purpose

Show more features from LSL to support reasoning about programs

2 Outline

Last week we showed how we can express specifications about programs and use check-contract to search for counter-examples to them by generating random input examples and running them.

This works quite well, and we’ll continue to use it, in more and more sophisticated ways, throughout the semester. Sometimes, though, the fact that we only check a certain number of random inputs may mean we won’t find a bug. For example, consider the following (pathological) "multiplication" function.

(: bad-mult (-> Real Real Real))

(define (bad-mult x y)   (if (= x 10417)       0       (* x y)))

(: bad-mult-prop (-> Real Real True))

(define (bad-mult-prop x y)   (= (bad-mult x y)      (* x y)))

(check-contract bad-mult) (check-contract bad-mult-prop)

2 success(es) 0 failure(s) 0 error(s) 2 test(s) run

It passes check-contract, since the random testing doesn’t happen to find the single input on which it doesn’t work. This is an artificial case, but often, bugs appear at edge cases, and code may work well in all other cases. Another common source of bugs are overflow or underflow bugs, where bugs only appear when numbers are too large (or small) to be represented accurately in the (fixed) space typically used for them. In those cases, the code may work well for all "normal" values but when confronted with a large value, it may fail.

To address this, in limited settings, there is another way that LSL can validate these types of properties: by calling out to an SMT solver.

A little background on SMT. SMT (Satisfiability Modulo Theories) is a generalization of boolean satisfiablity. You will probably learn a bit more about it in either a theory of computation course or maybe an algorithms course, but the problem, stated simply, is:

Given a formula in propositional logic, that is, built with variables (e.g., P,Q,R,\ldots), operators (usually just \wedge,\vee,\neg), and parentheses, is there a truth assignment that makes the formula true?

A naive approach is simple: go through every possible assignment of variables, and see if any satisfy the formula. While this is obviously correct, it is also (nearly as obviously), exponential, since there are 2^n possible assignments (each variable has two possible assignments, so if there are n variables, 2 * 2 * \ldots 2 = 2^n).

For large formulas with lots of variables, this is clearly a bad idea. So why are we talking about this?

Well, two things come together to make SAT probably the most important problem in computer science.

First, an old theorem, proved independently in the early 1970s by Stephen Cook and Leonid Levin, showed that any problem in the complexity class NP could be reduced, or translated, to SAT in polynomial time.

It is thus the quintessential hard problem, but also, incredibly general, and if you have taken or do take a theory class, probably one of the things you will do is reduce some other problem to SAT.

But also, in the last few decades practioners have figured out how to solve most examples of SAT very very quickly. So while in the worst case (what the proofs from theorists show) it is incredibly hard, in many cases (including, as it turns out, many important and useful ones), we can do it quite quickly.

Example reduction

Consider a map coloring. If you want to assign different colors to adjacent squares on a map.

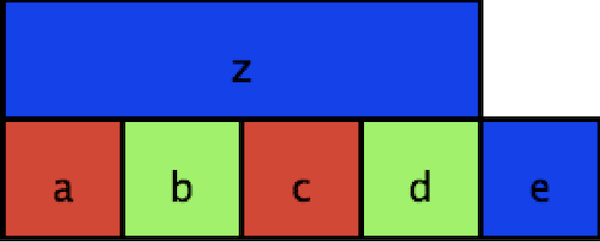
You could express this problem as a SAT problem by defining variables for whether each labeled square is colored red, blue, or green. Then, you need to not only show that a square can only be one color, but that each pair of adjacent squares, you could add a clause that says that the two squares cannot be the same color.

We can express this by the following. First, we show that we assign exactly one color to each square, by showing that one of the three variables (a_r, a_g, a_b) is true, but not more than one (by ensuring that for every pairing, at least one is false). \begin{array}{l} (a_r \vee a_g \vee a_b) \wedge (\neg a_r \vee \neg a_g) \wedge (\neg a_r \vee \neg a_b) \wedge (\neg a_g \vee \neg a_b) \\ \end{array}

We have to do this for each of our squares. This amounts to allowing an assignment, but doesn’t yet cover the adjacency requirement.

\begin{array}{l} (b_r \vee b_g \vee b_b) \wedge (\neg b_r \vee \neg b_g) \wedge (\neg b_r \vee \neg b_b) \wedge (\neg b_g \vee \neg b_b) \wedge \\ (c_r \vee c_g \vee c_b) \wedge (\neg c_r \vee \neg c_g) \wedge (\neg c_r \vee \neg c_b) \wedge (\neg c_g \vee \neg c_b) \wedge \\ (d_r \vee d_g \vee d_b) \wedge (\neg d_r \vee \neg d_g) \wedge (\neg d_r \vee \neg d_b) \wedge (\neg d_g \vee \neg d_b) \wedge \\ (e_r \vee e_g \vee e_b) \wedge (\neg e_r \vee \neg e_g) \wedge (\neg e_r \vee \neg e_b) \wedge (\neg e_g \vee \neg e_b) \wedge \\ (z_r \vee z_g \vee z_b) \wedge (\neg z_r \vee \neg z_g) \wedge (\neg z_r \vee \neg z_b) \wedge (\neg z_g \vee \neg z_b) \\ \end{array}

How do we handle adjacency? Well, we want to know that if two squares (say, a and b) are adjacent, then they cannot be the same color. So, for each color c, we add a clause \neg a_c \vee \neg b_c. Why does that work? If a_c is true, that means a has been colored with color c, which means \neg a_c is false, so for the clause to be satisfied, \neg b_c has to be true, which means that b_c must be false, and thus b cannot be colored with color c.

This means the rest of our complete formula is:

\begin{array}{l} (\neg a_r \vee \neg b_r) \wedge (\neg a_g \vee \neg b_g) \wedge (\neg a_b \vee \neg b_b) \wedge \\ (\neg a_r \vee \neg z_r) \wedge (\neg a_g \vee \neg z_g) \wedge (\neg a_b \vee \neg z_b) \wedge \\ (\neg b_r \vee \neg c_r) \wedge (\neg b_g \vee \neg c_g) \wedge (\neg b_b \vee \neg c_b) \wedge \\ (\neg c_r \vee \neg d_r) \wedge (\neg c_g \vee \neg d_g) \wedge (\neg c_b \vee \neg d_b) \wedge \\ (\neg c_r \vee \neg z_r) \wedge (\neg c_g \vee \neg z_g) \wedge (\neg c_b \vee \neg z_b) \wedge \\ (\neg d_r \vee \neg e_r) \wedge (\neg d_g \vee \neg e_g) \wedge (\neg d_b \vee \neg e_b) \wedge \\ (\neg d_r \vee \neg z_r) \wedge (\neg d_g \vee \neg z_g) \wedge (\neg d_b \vee \neg z_b) \\ \end{array}

Now, if we can find a satisfying assignment to this formula, we know that we can color the map. And in particular, the coloring will be given by the assignment: if a_r is true, a is red, if b_g is true, so b is green, etc.

It’s important to note, of course, that there may be many satisfying assignments, and the solver may only find one of them, or report that no such assignment is possible.

Reduction for properties about programs

While in theory SAT can be used to express an incredibly wide variety of properties, one of the most important practical uses is to express properties about programs or systems. One mechanism, called Bounded Model Checking, involves taking a program, transforming it into a version that works for some finite input k, and then checking some property about that program.

That can result in three possibilites: the property may be violated (in which case, a bug has been found for small input), the finitization fails (i.e., if a loop was unrolled n times, but that wasn’t sufficient for even the small input), or no problem is detected. In the first case, a bug has been found. In the second case, the program errors because of the loop invariant, but not because of buggy behavior. However, since only a finitized version of the program was run, it’s possible that there still exist bugs on larger inputs. In the last case, no bug is detected, and so we know no bugs exist for all small inputs, but may still exhibit bugs on larger inputs than we test on. One of the hypotheses of Bounded Model Checking is that if the program is correct for small inputs, it will be correct for larger inputs.

How this relates to LSL

As it turns out, LSL has built-in support to automatically do these sorts of reductions. Under the hood, is uses a state-of-the-art tool called Rosette, which can translate a subset of the programs you write into formulas and run them against an SMT solver (by default, the solver Z3).

The way this works is that, provided the input to a function is finite, rather than running check-contract, you can run verify-contract.

If we return to our (trivially buggy) pathological multiplication function, we can find the bug easily:

(verify-contract bad-mult-prop)

-------------------- interaction-area tests > Unnamed test FAILURE params:     '(#<procedure:...yntax/interface.rkt:83:7>) name:       verify-contract location:   eval:6:0 discovered a counterexample   counterexample: (bad-mult-prop 10417.0 -1.0)   error:     [assert] bad-mult-prop: contract violation       expected: True       given: #f       blaming: program (as server) -------------------- 0 success(es) 1 failure(s) 0 error(s) 1 test(s) run

Note how it shows the counter-example when it finds a verification failure.