Assignment 8: Iterators and Sameness, and Finishing Games🔗

Goals: Further practice with ArrayLists; mutable worlds.

Instructions🔗

The submissions will be organized as follows:

• Homework 8 Problem 1: The Knitting.java file.

• Homework 8 Problem 2: Rush Hour part 3

Due Date: Thursday, March 21st at 9:00pm

Problem 1: Knitted fabric🔗

In this problem you are going to design two distinct but related data definitions: one to describe knitted fabric, and another to describe the instructions needed to actually make a fabric. Read the entire problem carefully before starting; you might otherwise jump to conclusions that are not warranted.

A knitted fabric is made up of two basic kinds of stitches: knits and purls. On the front side of the fabric, a knit stitch looks like a V, while on the back side it looks like a -. Purl stitches are the opposite: on the front side of the fabric they look like a -, while on the back side they look like a V. A knitted fabric is made up of rows of these stitches, typically starting from the bottom and working upward (e.g. from the waistband of a sweater up to the neck), and combining different stitches in different pattern on different rows naturally produces different textures of results.

Design a class KnittedFabric (and any helper classes) to represent a knitted fabric. (Hint: your design should not need any fields of type String.) Your KnittedFabric class must include a constructor with zero arguments, to create an empty fabric.

Design a method KnittedFabric addRow(Iterator<IStitch> rowIter) that takes in an iterator of stitches, from left to right on the front side of the fabric, and adds that row of stitches to the current fabric — and then returns the current fabric, so that you can add another row to it easily.

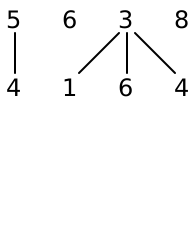
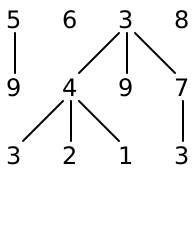
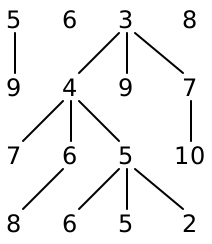
Design a method String renderFabric that draws your fabric as a string of text. You can see some examples of rendered fabrics below.

Design a method sameFabric that checks if two knitted fabrics look the same. Keep in mind, you might be looking at the front side of one fabric and the back side of the other, but they might be the same fabric if you turn them both to face forward — the following two fabrics are the same:

VVV----V    and     -VVVV---
---VVVV-            V----VVV

Design the class KnitFabricInstructions (and any helper classes needed) to represent knitting instructions for a full fabric. You should at minimum have classes that represent the three kinds of instructions, single rows of instructions, and an entire fabric’s worth of instructions. Your KnitFabricInstructions class must have a zero-argument constructor that creates an empty set of instructions.

Design a method KnitFabricInstructions addRow(Iterator<IInstruction> instructions) that adds a row of instructions to the growing fabric. Note that the instructions should be interpreted based on whichever side of the fabric is next: either right-to-left instructions for a front-side row, or left-to-right instructions for a back-side row. Like the other addRow method, this one will return the current set of instructions, so that you can continue add more rows of instructions.

Design the method KnittedFabric makeFabric() that follows the instructions and generates the knitted fabric result. (Hint: you will likely want an accumulator parameter in a helper method somewhere; that accumulator likely will be a boolean; you may need other accumulators or other helpers as well.)

Design the method boolean sameInstructions(KnitFabricInstructions other) that decides whether this set of instructions and that set of instructions will produce the same final fabric. As a tiny example, “knit 3, purl 3, knit 3, purl 3” will produce the same fabric as “((knit) 3 times, (purl) 3 times) 2 times.”

Problem 2: Rush Hour, Part 3🔗

In the previous part of Rush Hour, you implemented player movement rules, added obstacles and irregularly-shaped levels. In this week’s exciting conclusion, you’ll create a variation on the game, and add a way to fix mistakes.

8.1 Klotski🔗

The general mechanic of “moving rectangular tiles in straight lines and trying to get a goal piece out the exit” has come up in lots of varieties over time. This week, you will extend your implementation to support Klotski, whose rules are similar to Rush Hour but with a few variations:

• Tiles can be 1x1, 1x2 or 2x2 cells large.

• Tiles can move in all four directions: left, right, up and down. They cannot turn or move diagonally.

• The goal is to get the 2x2 square out the exit.

• No other tiles can be removed from the exit. (This would make the game somewhat trivial!)

Here are two Klotski boards to get you started:

In both of these levels, the goal is to get the red square out the exit.

To enter these worlds as strings, extend your string-parsing such that

• "." represents a 1x1 piece

• "S" represents a 2x2 piece

NOTE: you will still need to support standard Rush Hour rules! You must be able to start a Rush Hour level and play by Rush Hour rules (where pieces can only move in one dimension) as well as be able to start a Klotski level and play by Klotski rules (as described above).

Exercise

Extend your implementation of Rush Hour to now support Klotski as well. Hint: You will likely need at least two World subclasses, to represent your distinct rulesets. Be sure to avoid as much code duplication as possible: your code will still be graded on its design and clarity.

8.2 Keeping score🔗

Exercise

Add a move-counter to keep track of the number of moves a player has made. A move should count how many pieces are selected and moved — merely selecting and deselecting a piece should not count as a move, and multiple consecutive moves of the same piece should count as only one move.

Show the score somewhere on screen. Lower scores are better!

8.3 Fixing mistakes:🔗

Exercise

It’s far too easy to make mistakes in this game, and it’s reasonable for a player to try out some ideas and then want to “go back” to a previous board state. Add an undo feature, that lets the player type "U" in order to rewind the game by one step. (Note that each undo should increase the player’s score! Undoing a bad move should not also rewind their score to something better.) Make sure that the game does not crash if the player tries to undo when there are not currently any moves to undo.

Have fun!

You can find a few more levels at https://josephpetitti.com/klotski. You might also try designing a few levels of your own – see if you can combine both Rush Hour mechanics (like trucks and obstacles and irregular board shapes) and Klotski rules, or Klotski shapes (1x1 and 2x2 pieces) with Rush Hour rules.

8.4 Submission notes:🔗

As with prior parts, you should submit an updated UserGuide.txt and Design.txt that describe how a user should play your game, and how a developer should read and understand your code. Make sure you submit all the necessary source and image files that your graders need in order for them to run your games.

There will likely be a self-eval questionnaire the day after this assignment is due. Much like the peer evaluations asked you to review each other’s code, this self-evaluation will ask you to justify your design choices against your Design.txt explanations, and to guide your graders to understand where to find particular test cases, examples, or other implementation choices.