Assignment 6: Mutable data
Goals: Constructing cyclic data; using mutation to design data structures; using mutation to solve algorithmic problems.
Instructions
As always, be very careful with your naming conventions.
The submissions will be organized as follows:
Homework 6 Problem 1: The Registrar.java file.
Homework 6 Problem 2: The Deque.java file.
Homework 6 Problem 3: The Huffman.java file.
Homework 6 Problem 3 – Examplar: The ExamplesHuffman.java file.
Huffman Examplar: Tuesday, February 25, 9:00pm.
Implementations: Friday, February 28, 9:00pm.
Problem 1: The Registrar’s Office
The registrar’s office maintains a great deal of information about classes, instructors, and students. Your task in this problem is to model that data, and implement a few methods on it. We deliberately do not give you the class diagram for this problem: from the description below, you should properly design whatever classes you think are relevant. Please use generic lists (i.e. IList<T>) for this problem.
6.1 Data constraints
A Course consists of a name (a String), an Instructor named prof, and a list of Students named students. No Course can be constructed without an Instructor available to teach it. Hint: Do you think that you should provide a list when constructing a Course? Why or why not?
An Instructor has a name and a list of Courses named courses they teach. Instructors are initially constructed without any Courses to teach.
A Student has a name, an id number (an int), and a list of Courses they are taking. Students are initially constructed without taking any Courses.
It should always be the case that any Student who is enrolled in a Course should appear in the list of Students for that Course, and the Course should likewise appear in the Student’s list of Courses.
It should always be the case that the Instructor for any Course should have that Course appear in the Instructor’s list of Courses.
6.2 Methods and examples to design
Design a method void enroll(Course c) that enrolls a Student in the given Course. Design any helper methods as appropriate.
Design a method boolean classmates(Student s) that determines whether the given Student is in any of the same classes as this Student.
Design a method boolean dejavu(Student s) that determines whether the given Student is in more than one of this Instructor’s Courses.
Construct example data consisting of at least five Students, at least four Courses and at least two Instructors. Test all your methods thoroughly.
Hint: you will at minimum need to design some kind of sameness-checking method for Students. We are not giving you any guarantees about how the classes in your program might be used or instantiated, so you must figure out what information should be used to define sameness, and justify your reasoning.
Problem 2: Who’s On Deque?
We would like to build a generic list in such a way that we can start either at the front, or at the back, and move through the list in either direction. Here is an example of such a list (shown here with Strings), drawn as an object diagram:
+---------------+
| Deque<String> |
+---------------+
| header ----------+
+---------------+ |
+--------------+
|
v
+------------------+
+---------->| Sentinel<String> |<-------------------------------------------+
| +------------------+ |
| +---- next | |
| | | prev ------------------------------------------------+ |
| | +------------------+ | |
| | | |
| v v |
| +--------------+ +--------------+ +--------------+ +--------------+ |
| | Node<String> | | Node<String> | | Node<String> | | Node<String> | |
| +--------------+ +--------------+ +--------------+ +--------------+ |
| | "abc" | | "bcd" | | "cde" | | "def" | |
| | next ----------->| next ----------->| next ----------->| next ----------+
+-- prev |<--- prev |<--- prev |<--- prev |
+--------------+ +--------------+ +--------------+ +--------------+Every Deque has a header that consists of the Sentinel node. This header field does not change, but the fields within the Sentinel node (that provide the links to the first and the last item in the Deque) can and will change.
Each data Node has two links, one to the next item in the list and one to the previous item in the list.
The Sentinel node is always present. It also has next and prev fields, which are consistently updated to link to the head of the list and to the tail of the list, respectively.
The Sentinel and Node classes both inherit from a common superclass (shown below), because the next or prev item after any given node may be either a data-carrying Node or the Sentinel marking the end of the list.
The list shown above has four data-carrying nodes and the lone sentinel. The empty list has just the Sentinel, and its links to the first and to the last item just reference the Sentinel node itself. So an empty list would have the following object diagram:
+---------------+
| Deque<String> |
+---------------+
| header ---------+
+---------------+ |
|
+--------+
+----+ | +----+
| | | | |
| V V V |
| +------------------+ |
| | Sentinel<String> | |
| +------------------+ |
+--- next | |
| prev ---------------+
+------------------+ +--------------------+
| Deque<T> |
+--------------------+
| Sentinel<T> header |-+
+--------------------+ |
|
+--------------------------+
|
|
| +---------------+
| | ANode<T> |
| +---------------+
| | ANode<T> next |
| | ANode<T> prev |
| +---------------+
| /_\ /_\
| | |
| +----+ |
V | |
+-------------+ +---------+
| Sentinel<T> | | Node<T> |
+-------------+ +---------+
+-------------+ | T data |
+---------+With one caveat, below.
6.1 Data definitions and examples
Define the classes ANode<T>, Node<T>, Sentinel<T>, and Deque<T>.
For Sentinel<T>, define a constructor that takes zero arguments, and initializes the next and prev fields of the Sentinel to the Sentinel itself.
For Node<T>, define two constructors: the first one takes just a value of type T, initializes the data field, and then initializes next and prev to null. The second convenience constructor should take a value of type T and two ANode<T> nodes, initialize the data field to the given value, initialize the next and prev fields to the given nodes, and also update the given nodes to refer back to this node. Throw an IllegalArgumentException in this constructor if either of the given nodes is null. (You can use if (theNode == null) { ... } to test for null-ness.) Note carefully the order of the arguments in this constructor! The order should match the class diagram above; getting the order wrong will result in oddly “backwards” lists.
For Deque<T>, define two constructors: one which takes zero arguments and initializes the header to a new Sentinel<T>, and another convenience constructor which takes a particular Sentinel value to use.
Make examples of three lists: the empty list, a list of Strings with the values ("abc", "bcd", "cde", and "def") shown in the drawing at the beginning of this problem, and a list with (at least) four values that are not ordered lexicographically. (Hint: If you’ve defined your constructors correctly, you shouldn’t need to use any explicit assignment statements in your examples class!)
(Make more examples as needed to test the methods you define.)
Name your examples class ExamplesDeque, and your first three examples deque1, deque2 and deque3.
6.2 Methods
Design the method size that counts the number of nodes in a list Deque, not including the header node. (I.e., just count the Nodes and not the Sentinel.)
Design the method addAtHead for the class Deque that consumes a value of type T and inserts it at the front of the list. Be sure to fix up all the links correctly!
Design the method addAtTail for the class Deque that consumes a value of type T and inserts it at the tail of this list. Again, be sure to fix up all the links correctly!
Design the method removeFromHead for the class Deque that removes the first node from this Deque. Throw a RuntimeException if an attempt is made to remove from an empty list. Be sure to fix up all the links correctly! As with ArrayList’s remove method, return the item that’s been removed from the list.
Design the method removeFromTail for the class Deque that removes the last node from this Deque, analogous to removeFromHead above. Again, be sure to fix up all the links correctly!
You probably have duplicate code in addAtHead, addAtTail, removeFromHead and removeFromTail. Revise your code to abstract out any duplication into helper methods —
most likely, helper methods on ANode<T> and its subclasses. These last two methods slightly break our claim above. Consequently, they’re not an ideal design for our interface, but they are better practice for the skills on this assignment than a more robust OOD approach to them.
Design the method find for the class Deque that takes an Predicate<T> and produces the first node in this Deque for which the given predicate returns true. (The Predicate<T> interface is predefined for us, just like java.util.function.Function<A, R> was from the previous homework. It is essentially the same as the IPred<T> interface from lecture, though the method name is slightly different:// Represents a boolean-valued question over values of type T interface Predicate<T> { boolean test(T t); } You’ll need to import this interface, and then define several classes that implement it, to test your code.)
If the predicate never returns true for any value in the Deque, then the find method should return the header node in this Deque, rather than return null. (Hint: think carefully about the return type for find!)
Design the method removeNode for the class Deque that removes the given node from this Deque. (Unlike removeFromHead or removeFromTail, this method does not need to return anything. Why?) If the given node is the Sentinel header, the method does nothing. (Hint: think again about the return type from find!) If you’ve revised your code to remove duplication as suggested above, this method should be very short and simple to implement.
Problem 3: Huffman Coding
A character encoding is a way of representing an alphabet (set of characters) with some kind of code. In computer science, that code is often made of single bits, 0s and 1s, since that is how all data is ultimately stored.
Unicode’s industry-standard encoding is what lets us have emojis. :-)
For example, if we had the following encoding:
Letter |
| Code |
a |
| 0 |
b |
| 1,0 |
c |
| 1,1 |
Then "abc" would be encoded as the five bits 01011, and 1110 would be decoded as "cb".
After all, there are far fewer short codes than long codes. Why?
While there are various properties that make Huffman codings interesting, the one we are most interested in is that it is a prefix code. This means that no encoding of one character is a prefix of any other character’s encoding. The example given above is a prefix code. The following, however, is not:
Letter |
| Code |
e |
| 0 |
f |
| 1 |
g |
| 01 |
What would 01 decode to, ef or g? Prefix codes help eliminate these types of ambiguities.
6.1 The algorithm
The best way to explain the Huffman coding algorithm is to illustrate it.
For example, say we begin with the following letters:
"a", "b", "c", "d", "e", "f"
Where each letter has the following relative frequencies:
12, 45, 5, 13, 9, 16
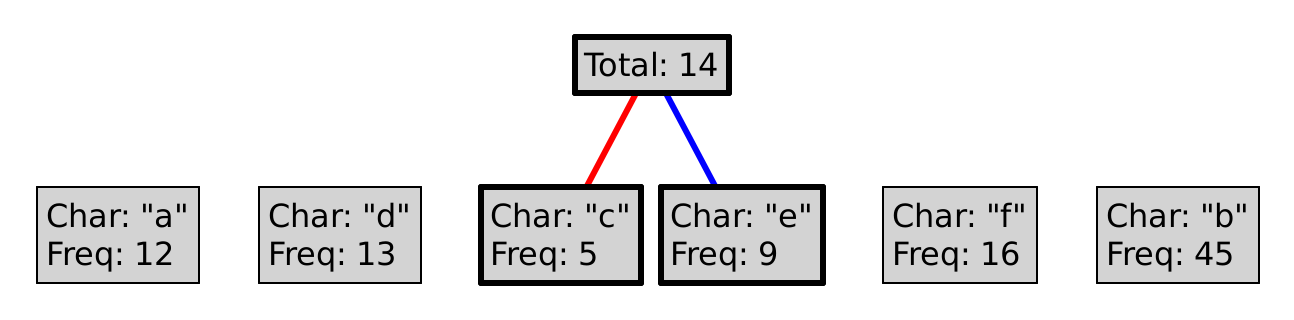
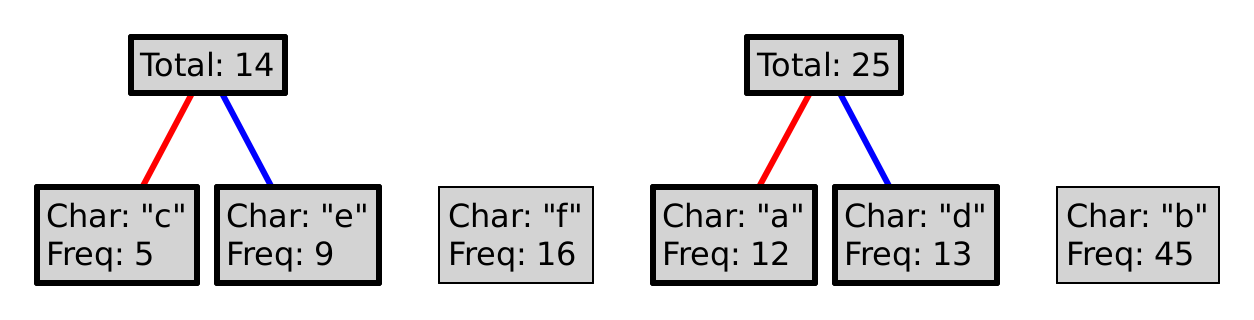
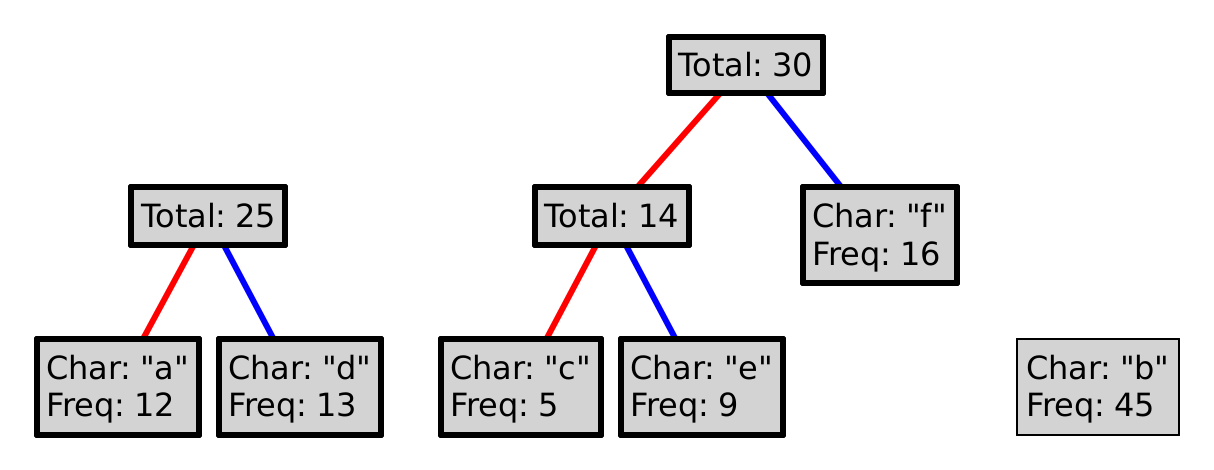
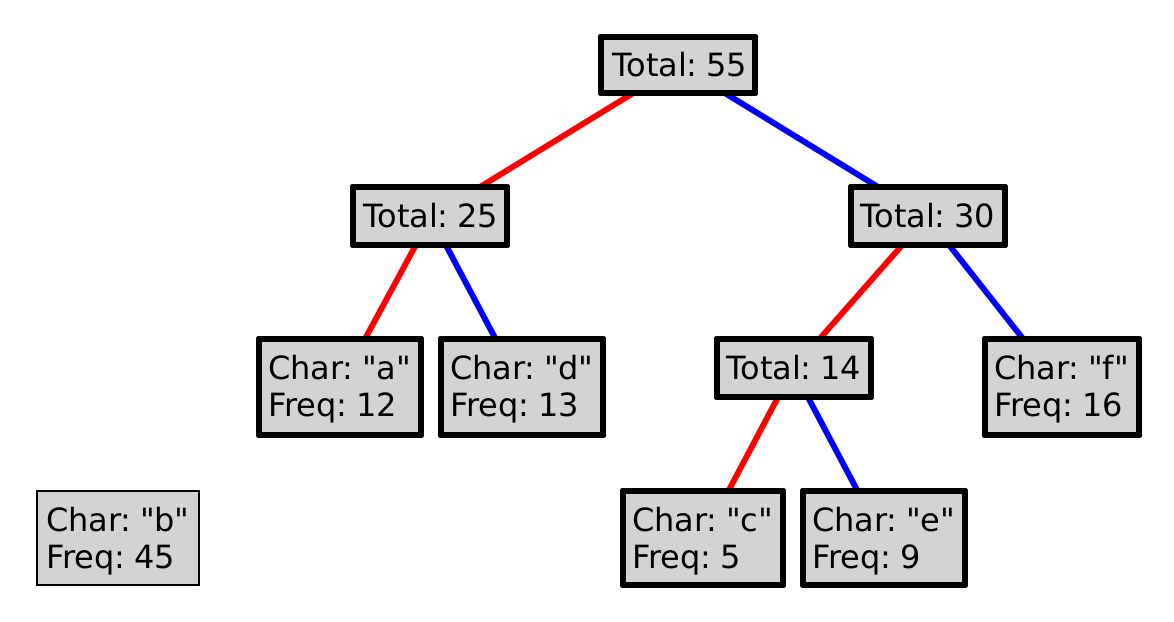
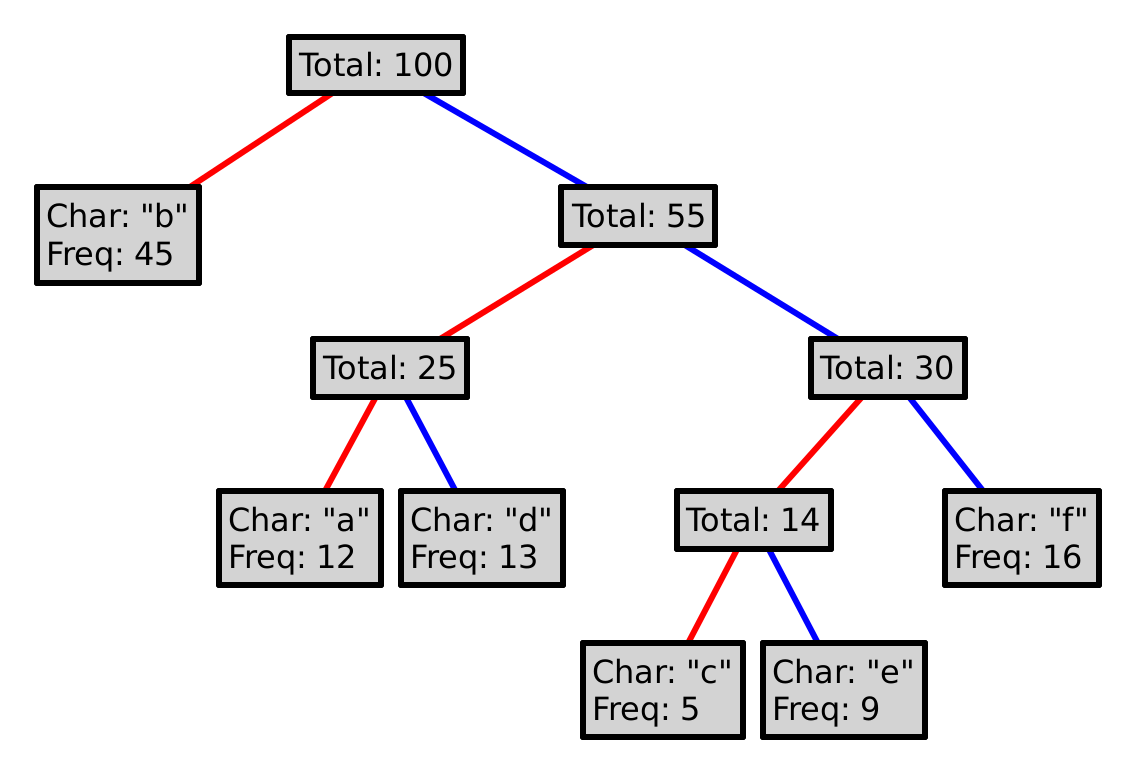


This process is guaranteed to produce a prefix code. Why? Could we choose red as 1, and blue as 0? Could we choose differently at every level of the tree?
To encode a character, follow the path from the root to the leaf with that letter, where a red line represents a 0, and a blue a 1. So, encoding "eba" with the tree above would produce 11010100. Decoding a sequence of 0s and 1s is (essentially) the inverse operation, so decoding 101111 would yield "df".
Composing the encoding and decoding operations in either order should produce what is effectively the identity function (on either strings or bit-sequences), but they aren’t quite inverse functions. Why not?
6.2 Data design and methods
Design the Huffman class, which should be constructed with two ArrayLists, one of strings and the other of integers (in that order), representing the letters of the alphabet in question and their relative frequencies. You may assume the integers are always positive and that the strings are always of size 1 (and never equal to "?"), but you should throw an IllegalArgumentException if the lists are of different lengths or if the length of the list of strings is less than 2 (after all, there wouldn’t be much point of encoding a 1-letter alphabet).
Your forest should be represented by an ArrayList of some kind. You may need a helper class; you may need multiple ArrayLists; the design is up to you.
In order for your encoded output to match ours, and therefore match the test cases, we need to specify how to sort the leaves and nodes. When sorting the initial leaves, you should use a stable sorting algorithm. This means that if two different elements have the same value for the purposes of sorting, their relative order in the original list should be preserved. (For instance, if two letters have the same frequency, then they have the same value for sorting even though they are not the same letter.)
Similarly, when you insert a new node into the forest, you should ensure that it appears as deep in the list as possible, so that if it ties with something else already in the list, the existing value “wins” and should come first. You should be sure to carefully test these properties of your sort, and you should not have to attempt to re-sort the entire list when inserting a new node.
Design the encode method, which takes a string and returns an ArrayList<Boolean>, where 0 is represented by false and 1 by true. If the string contains any character not in the alphabet, an IllegalArgumentException should be thrown with the exact error "Tried to encode <the character in question> but that is not part of the language.", where "<the character in question>" is replaced with the first character in the string that is not in the alphabet.
Design the decode method, which takes an ArrayList<Boolean>, where 0 is represented by false and 1 by true, and returns the string represented by this encoding. If at the end of the list of booleans you run out of booleans before you can reach a terminal node in the tree, you should end the string with a single "?". For example, in the above tree, the list of false, true, false, would decode to "b?".
(Hint: for a change, we’re not treating Strings as primitive data: you’ll need to search around the methods on Strings to find one that helps get length-1 substrings out from the string. You should not need to work with Java chars for this assignment.)
Examplar submissions
As before, we are going to supply an additional submission on Handins. You will write examples and test case sagainst a placeholder of the Huffman class, and we will run your test cases against the wheats and chaffs for this problem.
Name your examples class ExamplarHuffman and start it as follows:
import huffman.*; import tester.Tester; class ExamplesHuffman { // your examples go here }