Homework 2b🔗

MUST BE DONE ON YOUR OWN.

Due Date Thu at 9:00pm (Week 2)

Purpose Practice with structs and conditionals

MAKE SURE YOU INCLUDE TESTS FOR ALL OF YOUR FUNCTIONS.

Submit all of the following in a single .rkt file to Handins. You will get immediate feedback and can resubmit.

Reminder: whenever a problem says to design a function, we expect to see the full design recipe followed – signatures, purpose statements, relevant templates, and sufficient examples, along with your actual solution.

Exercises

Exercise 1 Finish the dist-to-0 function that we began in class today that uses the Posn data definition (and the posn struct) from class, instead of three separate numbers as had been done on the previous homework.

Exercise 2 The Euclidean distance above is sometimes described as the “as the bird flies” distance, since birds can fly over any ground-level obstacles. But for people walking around in cities like Manhattan, where the roads are laid out in a rectangular grid, the Euclidean distance doesn’t really describe the distance a person walks from one point to another, following the streets. Note that there are multiple paths: one can take a "direct" strategy, going as far left (or right) as needed, followed by as many up (or down) steps as needed. You could also take a "random walk", going some blocks leftward, some upward, and so on until the destination is reached. But it doesn’t make sense to take both left and right steps, or both up and down steps, since such detours “cancel each other out”.

Stop! Assuming you take no detours, does it matter which strategy you follow?

The Manhattan distance between two points measures this detour-free length of a path between two points that follows the rectangular grid of streets found in cities (like Manhattan).

Design the function manhattan-distance, which computes the Manhattan distance of the given Posn to the origin.

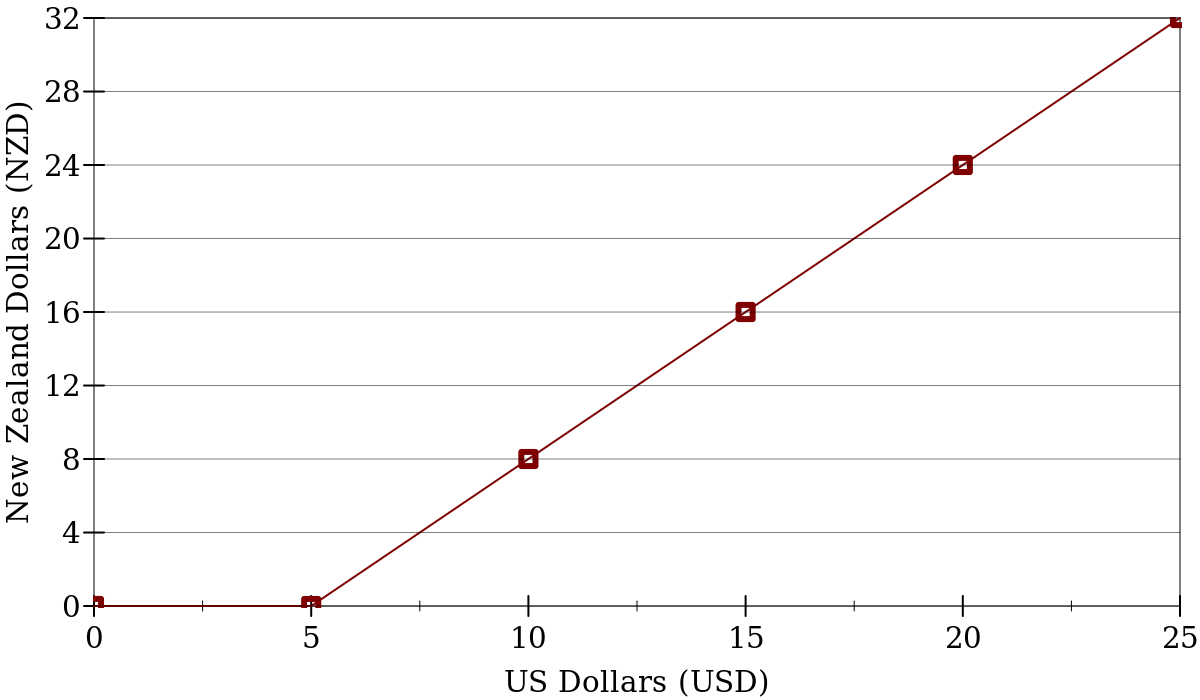
Exercise 3 When planning a vacation to another country, it’s a good idea to check the exchange rate between local and foreign currencies. For instance, one currency-exchange service provides the following chart for Americans traveling to New Zealand...

Notice that there is a flat fee charged for service as well as a conversion rate for each dollar being converted. For example, anything less than 5 USD gets eaten by the service fee, but 10 USD gets you 8 NZD.

Design a function, usd->nzd, to convert from US Dollars to New Zealand Dollars.

Hint: it can be useful to write out a table of input/output pairs to help understand these types of mathematical relationships (and these can then provide great tests!)

Exercise 4 Design the function leap-year? which determines if a natural number represents a leap year in the Gregorian calendar.