Homework 2a

MUST BE DONE WITH YOUR PARTNER

Due Date Tues at 9:00pm (Week 2)

Purpose Start working on course project, practice with design recipe

Submit all of the following in a single .rkt file to Gradescope You will get immediate feedback and can resubmit.

Exercises

Everyday I’m Shuffling

; A CSG (CoinShuffleGame) is a (make-csg CoinOrFalse CoinOrFalse CoinOrFalse)

(define-struct csg [left middle right])

; and represents the three cups in a coin shuffle game, and what is under them

; A CoinOrFalse is one of:

; - #false

; - Number

; and represents either no coin or the coin's monetary value

; A Guess is one of:

; - "left"

; - "middle"

; - "right

Exercise 1 Provide examples and templates for the above data definitions. Recall that when data definitions refer to other complex data types, the template must reflect this by calling the appropriate template.

Exercise 2 Design a function, shuffle-right, which moves all cup values in a CSG to the right. The right cup’s contents should loop back to the left cup.

Exercise 3 Design a function, csg-value, which given a CSG and a Guess, outputs the monetary value of the guessed cup. No coinage is worth 0.

Exercise 4 Design the function inflation, which given a CSG and a number, adds that monetary value to all of the coins in the cup, and leaves empty cups as is.

Course Project

Over the course of the semester, you will design a game called Shannon, in which players use gates from Boolean logic (AND, OR, NOT) and to solve puzzles on space-constrained grids.

The puzzles have the following form: a grid has a fixed number of input & output wires, and a Boolean function that is the goal of the game. The goal of the game is to add gates & connective plates in order to implement the given function. Given infinite space (and in 3D), this would be relatively easy, but the space and planar constraints can make it possible to create somewhat tricky puzzles.

For example, a simple example grid might be:

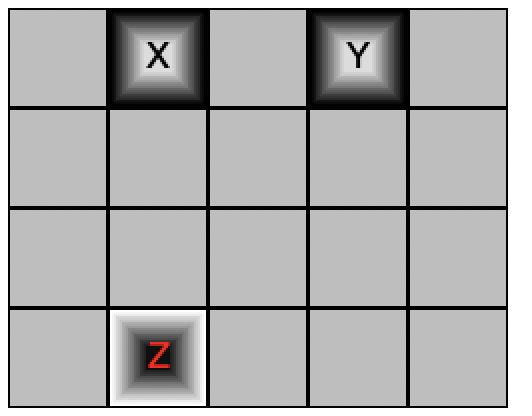
Where the black letters are input wires, the red are output, and the function was:

(define (f x y)

(not x))

This puzzle could be solved by connecting the input to output with conductive plates (which allow boolean values to flow across them in any non-diagonal direction) and a single NOT gate that is oriented down, e.g., as follows:

In this assignment, you will start designing data to represent various part of the game.

Exercise 5 First, design data to represent a single "Cell" of the grid, which may hold an input/output wire (e.g., "X", "Y", "Z" above, distinguishing whether they are input or output), a gate (AND, OR, NOT, with orientation), a conductive plate, or be empty.

Exercise 6 Now, design a function, "cell->image", that turns a cell into an image, suitable for displaying to a player of the game. You should first define a constant "CELL-SIZE" that is the dimensions of the cell. You may be as creative as you’d like (you do not have to follow our design above), but be sure that each one is the same size.