Lecture 4: Recursive data structures: Lists (& Abstract Classes Review)

How to represent lists of data.
Methods on lists.
Abstracting behavior.

4.1 Brief Review: Abstract Classes

We saw in Lecture 3: Representing more complex forms of data that an interface and abstract classes can be used to specify the protocol for types to implement specific behavior. Depending on the situation either approach towards design - using interfaces and/or abstract classes - is appropriate. During Analysis and early Design, one may take a "top down" approach and use abstract classes to help organize and understand the domain more effectively. An abstract class might begin as a placeholder for a hierarchical concept, and it may disappear as design iterations fold those concepts into more direct approaches for implementation. On the other hand, during later design and iterations of implementation, one may take a "bottom up" approach to re-factor the existing classes and "push" common, reusable code into an abstract class.

Some general observations for design decision-making (with the understanding that there is no one correct answer for all cases)

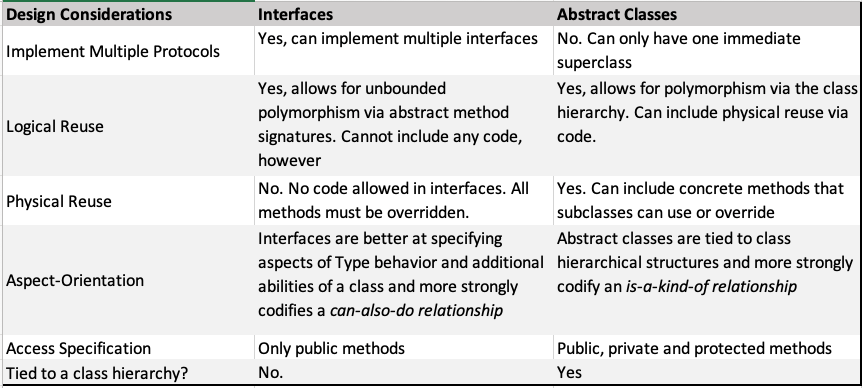
4.2 Quick Peek: Static

So far, we have discussed classes, objects, instance data (the attributes specified by a class and "realized" when an object is instantiated from the class blueprint), and instance methods (the functions specified by a class and invoked by each instance to do something). Thus, we have (up to now) used classes as a blueprint for how to make and use objects. In addition to this viewpoint, object-oriented systems also support the concept of classes themselves having behavior and data for use by its instances and other clients. The breadth of support for class-related behavior and data varies from one OO language to the next. But in general, this facility allows class-scoped data to be accessed before/without any objects created. In Java, class data and class methods are created with the static keyword.

When a variable is declared as static, then a single copy of variable is created and shared among all objects at the class level. All instances of the class share the same static variable, so these "class variables" (rather than "instance variables") are similar to class-scoped global variables.

Note that class methods (static methods in Java) can only access class variables (static data in Java) since there is no guarantee that an object will actually be in existence when the method is invoked.

Note the use of the fully-qualified name by using the className dot static-method format. Again, there is no OBJECT invoking this method; we are accessing it through the class.

When would you use static/class methods and data? Certainly when you would have leaned towards using a global variable, class data (and the class methods to access that data) are a suitable choice. Later in this course when we cover design patterns you will explore the use of class methods for the purpose of creation and "factory" approaches to give your systems flexibility in how objects are instantiated.

4.3 Recursive data structures

We saw in Lecture 3: Representing more complex forms of data that an interface can be used to represent data that is one of several different forms. Sometimes, some of those forms refer to themselves or other forms of the data type adhering to the protocol (common list of methods) and implementing the interface. If so, this is a recursive structure.

4.4 A collection of books

We use a simplified variant of a book representation. This is included in the Book.java file in the accompanying code. Specifically, the Book class has the following structure:

Suppose we wish to keep track of several books. The simplest way to do this is to create a list. There are several ways to represent a list of something, one of which is a linked list.

A linked list is made of individual nodes. A node in the list contains the data (in our case, the book) and points to the next node in the list (the link). The last node in such a list is often empty, signifying the end of the list. Thus the linked list stores the data sequentially.

4.4.1 Data representation and operations

A linked list is an example of a self-referential data structure, i.e. a recursive structure. As the illustration above shows, a list can be thought of as a single node followed by “the rest of the list”. An empty list consists simply of an empty node. Thus a list can implement a protocol that handles that variety. A list can be (a) an empty node or (b) a node with an element of data and another list.

We’d like to define the following operations on a list:

• Count the number of books in the list

• Calculate the total price of the list of books

• Print the list of books

• Get a list of books that were published before a given year

• Sort the list of books by price

This is denoted by the following class diagram

and by the following code snippet:

An EmptyNode object represents an empty list. It also represents the end of a list. This is sometimes referred to as a sentinel representation, in contrast with ending a list in null. Having an explicit empty object in the end helps in implementing several operations, as we see in this lecture.

4.4.2 Examples

Here are some examples of lists of books:

4.4.3 Counting the number of books

For the above list, we expect the following results for counting:

When a structure is recursive (as this list is), it helps to express an operation on it recursively as well. Often operations on recursive structures are recursive themselves as they exploit the structure.

We may describe counting the number of books as: “the number of books in the list can be obtained by counting the first book, and adding it to the number of books in the rest of the list.” As the base case, if the list is empty, the number of books is 0. Since EmptyNode represents an empty list, the base case is the implementation of count() in that class, while the recursive definition is the implementation of count() in the ElementNode class.

How do we know the recursive method will work? this.rest is an IListOfBooks and is guaranteed to have a count() method.

Here are the JUnit tests for this method:

4.4.4 Counting: Take 2

Look at the implementation of the count method in the ElementNode class.

This method recursively calls itself (for the next node) and then adds 1 to the result. In other words it “builds” the count as the recursion unravels (from back to front in the list). Another way to think about this operation is to build the count as one proceeds from the beginning to the end of the list.

We can do this by keeping track of the “current” count of books from the beginning of the list to the node where we currently are. Before proceeding to the rest of the list, we add 1 to this count. Thus when we reach the end of the list, the value of this count is equal to the number of books in the list. In other words, we accumulate the count as we traverse the list from front to back.

Where do we store this “accumulator” so that we can access it from the counting method? A common approach is to store this accumulator as a “global” variable. Besides the fact that Java does not support global variables, using global variables is usually bad design (its use is justified only when a value needs to be accessed from several places, and in that case the design is likely flawed). Instead, we can pass this accumulator as an argument to our method.

We begin by declaring a helper method for our nodes.

Declaring a helper method in the interface makes it public, which is bad design. A better design would be to use an abstract class and put this method there as protected.

How do we implement this method in the EmptyNode class? Our above logic says that when we reach the end of the list (i.e. the EmptyNode object) the value of the accumulator is equal to the number of books. Therefore this implementation simply returns the accumulator.

How do we implement this method in the ElementNode class? We add 1 to the accumulator and pass it along.

Finally, we make the count method use this helper method.

4.4.5 Unravel or accumulate?

Both approaches result in the correct answer, so which one is “better”?

We observe that the first implementation builds the count as the recursion unravels (back to front). No work is done before the recursive call is made and all the work is done after the recursive call returns. The accumulator implementation builds the count as the recursion proceeds (front to back). All the work is done before the recursive call is made, and nothing after it returns. This last observation implies that the last operation that countHelp does is to call itself recursively. This is referred to as “tail-recursive.”

There is one programming benefit to tail-recursive operations: they can be replaced with a non-recursive construct (usually loops). Recursive implementations, when done correctly, are elegant but suffer from one possible problem: stack overflow. This occurs where there are too many recursive calls resulting in filling up of the program stack. In this particular method, the number of recursive calls is equal to the size of the list, so we may encounter this problem for large lists.

How can tail recursion be replaced? This tail recursive implementation can be described as “start with 0, increment the accumulator by 1 for every non-empty node in the list” This description readily reveals that a loop can be used for this purpose. In fact most modern compilers automatically recognize tail recursion and optimize the generated code. It is also possible to automatically transform code into tail recursion and then optimize it. Some aggressive compilers, especially in functional programming languages where recursion is ubiquitous, include such features.

Do Now!

Try to make the countHelp method non-recursive.

Beyond the programming and efficiency benefits, the accumulator method is an important design technique by itself. Depending on the actual operation, it may be easier to think of accumulator-type design.

4.5 Printing the list of books

We can “print” the list of books by simply writing a toString method for its nodes that creates and returns a string of a specific format.

Before we write the toString() method we need to illustrate how we’d like the output to look. We would like each book to appear within a set of parentheses, with all books in a single line. Here is an example:

Let us try expressing this operation recursively as well. Its objective is to generate and return a string. One way to express it would be “The string representing the contents of a list can be constructed by creating a string representation of the first book, and appending to it the string that represents the rest of the list.”. If the list is empty (base case) then an empty string is returned.

This expression is very similar to that of the count(), and we expect its implementation to be similar as well. How do we create a string representation of a book? We could get all the data from the Book object and create the string ourselves, or we can delegate to ...the toString of the Book class!

Do Now!

Try to rewrite toString using an accumulator design.

Here is the test for this method:

4.5.1 Computing the total price of all books

Do Now!

Express this operation in a recursive way, and design an implementation for it

4.5.2 Getting a list of all books published before a given year

This method requires us to assemble a list of only those books in the original list that were published before the given year. For each node that contains a book, we must decide whether the book in that node should be included in our resulting list or not. We can compare the year of publication of the book with the given year directly, or we can delegate this determination to the Book class itself, as a method boolean before(int year).

Can we express this operation recursively as well? Here is one way: “the list of books published before a given year is made of (a) the first book in our list if it was published before the given year, followed by such books in the rest of the list or (b) simply such books in the rest of the list, if the first book was not published before the given year.”

4.5.3 Sorting the list by price

Sorting, or arranging in an increasing/decreasing order is a very common operation for lists. At the lowest level, it requires comparing two things in the list (in our case, comparing books by price) so that we know their relative order in the list. There are many different ways to sort a list. Here is one: the list is recursively defined as the first book, and the rest of the list (the structure of ElementNode). Imagine if the rest of the list was already sorted as how we want it. How can we use it to obtain the entire sorted list? We must insert the first book into the sorted list in such a way that the resulting list is sorted. This insight gives us the recursive expression for this operation: insert the first book into the sorted rest of the list. How do we sort the rest of the list? We see that sortByPrice() exists for this.rest, so we already have a way to do that!

We’re almost done–we need to implement the insert(book} method in both EmptyNode and ElementNode. Notice that the above code suggests that the insert method must return the resulting list. Thus its signature will be IListOfBooks insert(Book book).

The result of inserting a book into an empty list is a list of one element and an empty node at its end. This leads to the following implementation in EmptyNode.

For the ElementNode class we must compare the book to be added to the book that is in the node. If the book in the node is cheaper, then the new book should be inserted in the “rest” of the list. If not, the resulting list will have this book at the beginning, followed by the existing list.

this.rest.insert(book) will not work, because this.rest is of type IListOfBooks! So we must add this method to the ILiIListOfBooks interface as well.

The missing piece is the cheaperThan in the Book class:

This technique of sorting a list is called insertion sort. It is relatively straightforward to implement recursively, but often not the best way (in terms of efficiency) to sort a list.

4.6 Abstracting behavior

4.6.1 Getting a (sub) list...

Consider a new operation for our list of books: "Get a list of all books that are written by an author with name ‘Rowling’".

We add this method to the IListOfBooks interface:

We can then implement it in the two implementations as:

When we compare this method with the allBefore method before, we see several similarities in code. First, the signatures are similar. Secondly their implementations in EmptyNode are identical. Most importantly, their (non-trivial) implementation in the ElementNode class is similar as well. The only difference is the use of the containsAuthor method instead of the before method. In turn, both these methods have something in common: they operate upon a Book object. This repetition will proliferate if we design similar operations: "Get a list of all books that cost less than $10", "Get a list of all books that are published after 1980", etc. This hints that we can abstract such operations so that we do not have to repeat their common parts.

At a higher level, the common aspects of all these methods are: Apply a test to the book at the current node, and do one of two things depending on the result of that test. We can abstract this into one method, if we have a way of "providing the test" to this method. The test is a method of the form:

We can "provide" a "test" to this method as any object that contains the above method within it. We formalize this in an interface.

A function that takes in some data and returns a true/false answer is called a predicate. The IBookPredicate interface defines a "function object," an object that serves as a "wrapper" for a predicate function.

Now we can abstract the "Get a list..." method as:

We can implement it as follows:

We can express "all books before given year" and "all authors with name ‘Rowling’" as two implementations of the IBookPredicate interface:

Getting all books published before 2000 changes from

to

and getting all books with the name ‘Rowling’ changes from

to

This design has three distinct advantages:

• All "Get a list of books that satisfy this condition" are implemented only once, so long as the condition is a predicate that takes a Book object as its only argument.

• The Book class need not be cluttered with specific predicates such as allBefore and containsAuthor. So long as there is a way to get an attribute, it is possible to write any predicate that uses it. This is both good and bad: we will return to this issue later.

• Since a predicate is a boolean condition, we can create compound predicates using logical operators. For example, we can combine the two conditions above to "get a list that contains books published before 2000 AND whose author is Rowling." Such a predicate can be implemented simply as a class that implements the BookPredicate interface, takes two other BookPredicate objects as input to its constructor, and returns their AND result in its test method.

We can standardize this code even more! It turns out that Java has an interface that represents a predicate, so we need not define our own. This is the Predicate<T> interface. Since our predicates operate on books, we use its Predicate<Book> form.

4.6.1.1 Java syntactic sugar

The classes BookBefore and BookWithAuthor seem somewhat excessive, because they have only one method in them (and the constructor to input the year and name of author). If they are instantiated only at one place, we can replace them with nameless, anonymous classes:

Since there is only one place where the class was used, we can write its entire implementation at its place of usage. We need not name the class as BookBefore: it suffices to say that we are implementing a class that implements the Predicate<Book> interface. Since the class is being defined here, it can access the variable year defined right outside it. Thus we can summarize this usage as Define data needed in the predicate, then define the predicate as an anonymous class.

Anonymous classes have the potential to clutter code, if they are verbose. Therefore they should be used only when both of the following conditions are fulfilled:

• The class is short (i.e. it has 1-2 methods, and all of them are short).

• The class will be instantiated only once (because it needs to be defined at the place of instantiation).

In our specific situation, this can be simplified even more. Similar to the name of the class (BookBefore), the name of the method inside it (test) is also redundant. This is because it is the only method required to be in that class (since it implements Predicate<Book>). In other words, instead of saying Call the test method of this object we can get away with saying Call the only method inside this object, that takes a Book object and returns a boolean. Such nameless methods are lambda functions. A lambda (nameless) function is useful only when it is the only one around. Starting with Java 8, lambda functions are supported in Java.

The part (Book b) is the signature of the (nameless) lambda function. The -> points to its implementation, which follows it. Since the implementation is only one line, we type it directly (otherwise use curly braces).

Let us summarize explicitly how this latest code works:

• The getList method expects a Predicate<Book> object. What it really cares about is a method that has a single argument of type Book, and returns a boolean.

• Our lambda function notation provides it with such a function, using the minimum notation (i.e. no enclosing class, no method because they are redundant)

• The getList method traverses the list, and at every non-empty node it passes the Book object to this lambda function and acts according to its result.

Use of lambda functions states our original purpose more succinctly and clearly: write a method that takes a (predicate) function as an argument and uses it. In Java, functions cannot be passed as arguments directly, because Java treats data and methods as two different things. Therefore we enclose the function inside a (Predicate) object, and then pass it around. Syntactic support for lambda functions just brings the Java code closer to its original intent.

Most functional programming languages do not distinguish between data and functions. Therefore this implementation would look more concise in such languages.

4.6.2 Sort by ...

Our sort method arranged books in the list in non-descending order of price. However we could also sort the same list in non-ascending order of price, or based on the author name or even year of publication. If we examine our implementation of sorting, we can observe that the ordering of books in the final list is decided by the cheaperThan method in the Book class. Therefore, in order to change our sorting method, we must provide a different way of comparing two books...and here is the opportunity for abstraction!

We need a standard way to compare two books. As before we can use the Comparable interface. The Book class could implement this interface in the form of a public int compareTo(Book b) method. However this implementation will contain (fixed) comparison between two books (e.g. based on price). We cannot change the criteria to compare books without editing the Book class. Moreover multiple criteria cannot simultaneously exist, because the Book class can implement the compareTo method only once.

Java provides us with another way for precisely this use-case: the Comparator<T> interface. This interface has one method:

that returns the result as an integer using the same convention as Comparable. We can implement a class (separate from Book) that implements the Comparator<Book> interface and provides this method. More importantly, we can write several such classes, each providing a different way to compare two books, without editing the Book class!

Do Now!

Re-implement the sort method so that it uses the Comparator interface somehow. Can you use Java 8 constructs to abbreviate the syntax?

4.7 Stating abstractions more formally

The abstracted forms of getList are examples of higher-order functions. A higher-order function is a function that takes another function as an argument, and possibly returns a function as a value. Designing an operation as a higher-order function offers a powerful means of abstraction. Higher-order functions are supported to some degree in many programming languages, often supported best by languages that support functional programming.

4.7.1 Filter

At a high level the getList method above is a special case of the following generic operation: Given a list, create a sublist of things in the original list that satisfy a given condition. This List => List operation is called a filter. One may think of a filter as a generic operation on a list, and returns a sublist of the same type. It takes the general form

List filter(List input, Predicate p)

4.7.2 Fold/Reduce

The count method above starts from an entire list and computes a single value. It can be characterized as a fold higher-order function (another name for it is reduce).

A fold operation is of the form List => value. A fold operation starts with an initial value, an algorithm to combine this initial value with elements in the list and return the combination. Examples of fold include counting the number of books in the list, calculating the total price of all books, determining if the list contains a book by Rowling, etc.

The two approaches to counting the books in the list described above are both fold operations. The accumulator approach builds the total as we traverse the list from left to right. This is called a fold-l operation. In contrast the non-accumulator approach builds the total right-to-left as the recursion unravels. This is called a fold-r operation. Both approaches use an initial value of 0 (the initial value of the accumulator in fold-l and the return value in the EmptyNode for fold-r). Both approaches do not explicitly take a function as an argument, but can be thought of as using the operation "add 1" on every element of the list.

It may be added that fold need not work only on lists: it works on most recursive data structures.

4.7.3 Map

Consider a new operation on the above list of books: return a list of all titles in the same order as the list of books. This is an example of a map higher-order function. In general a map operation takes in a list and returns a list of the same size, but possibly of a different type. The function that a map applies to each element of the list can be thought of as mapping the element to another element.

Higher-order functions have given rise to the popular "Map Reduce" programming model, which is used to process large data using parallel algorithms and architectures. It is based on the observation that a lot of operations on large data can be termed as a “map” (a combination of the map and filter operations above), followed by a “reduce” (to summarize the result). As a simple example, given a list of user profiles on Facebook, finding the average number of posts by female users would amount to summarizing users as a list of (gender, number of posts) using a map, selecting only females using a filter, and then averaging the number of posts on the result using a reduce/fold. In a language that supports higher-order functions, this can be as simple as (in pseudo-code)