Lecture 3: Representing more complex forms of data

Overview

We have seen how to write classes to represent simple data, and how to write methods for such classes. We will now see what options Java gives us for some other forms of data.

3.1 Representing data that have finite, specific values

We designed the Book class to represent a book. Let us add more data for a book: the manner in which it is available to buy. A book can be bought in several forms: hard cover, paperback, kindle, etc. How can we represent this information in the Book class?

One option may be to represent this data as a simple number, and associate its values with specific forms of books. A value of 1 means Paperback, a value of 2 means Hard cover and a value of 3 means Kindle. Although we can make our class work with such a representation, it has several problems:

• How may an object communicate this information to an outside (client) class? We can write a getBookType that returns this number, but then the client must know what exactly the number means. We may return it as a String to be more descriptive. This approach is fraught with other problems: what if there is a difference in spelling?

• An integer has more than 3 valid values. What if this number is set to a value other than 1, 2 and 3? What will that represent? This is a bigger problem, because it hints that our way of representing this data is not accurate.

3.1.1 Enumerated types

The form of book is information that has a unique property: it can be one of a finite set of values, nothing else. Such type of data is common: days of the week, months of the year, types of chess pieces, sizes of ice-cream, etc. Java allows us to define a special type for such data: enumerated type.

We can define a type TypeOfBook for the form of book:

in a file TypeOfBook.java. Then we can change our Book class:

In the above code snippet the field bookType can have one of only three values: TypeOfBook.HARDCOVER, TypeOfBook.PAPERBACK and TypeOfBook.KINDLE. Attempting to assign it any other value will give us an error!

We must now modify the toString method of the Book class to include this information. We would like to convert these values into strings: “Hard Cover”, “Paperback” and “Kindle”.

In the above way we can check whether enum-type fields have specific values.

3.1.2 The switch statement

Notice the if statements in the above toString method: it is checking for specific values, and then doing certain things. There is a neater way of writing this in Java: the switch statement. The switch statement is of the form:

The above statement breaks down specific values of id into cases. When this program is run, Java will check if the value of id is value-one. If so, it will execute [do-something 1]. If it is not, it will check if the value of id is value-two, and so on. If the value of id isn’t any of the cases it will reach the (optional) default case and execute [do-something-none-of-the-above].

The case statements tell it where to “enter” the code, but not when to leave. Thus if id==value-one it will execute [do something 1] but stop checking other case statements. The break statement at the end causes it to come out of the switchstatement. Without it it would execute [do something 2] and so on, as it is no longer checking the case statements once it finds a successful one! So remember to add a break at the end of each case.

We can use switch in the above toString as follows:

In this case there is no need for a default as switch statement has a case for every value of the enumerated type and the enumerated type ensures that there is no other valid value for bookType.

What kinds of types can be used with switch? We can use types for integral numbers (i.e. int, long, etc.), characters (char), enumerated types and starting with Java 8, we can also use String. Read more about the switch statement in the Java switch tutorial.

3.2 Union data

Boston has the subway system for the city area and the commuter rail system for the greater Boston area. Although the trains and these stops are different, they both serve the same purpose. Stops in both systems are called “station”. Thus, a station can be a commuter station or a subway station. Both kinds of stations have names and the names of the lines they serve, and sell tickets. They also have unique characteristics. This is an example of a union data type.

There are many examples of union types: chess pieces, types of shapes, types of employees in a company, etc. They have some things in common: they have some common attributes and behaviors, and others that are unique. How does one capture this relationship between them?

3.2.1 Shapes

Consider two kinds of shapes: circle and rectangle. We can represent them using two classes: Circle and Rectangle. Both shapes have a reference position (center for the circle, bottom left corner for the rectangle). Being shapes, it is possible to compute the area and perimeter of either of them. Similarly we can resize both of them, and compare them to each other in terms of their size. When we start thinking about how to represent these shapes using classes, a good place to start would be to identify what are operations that make sense for both of them. This set of common operations relates them to each other. The following set of methods emerge:

• A method to compute and return the area of the shape.

• A method to compute and return the perimeter of the shape.

• A method to compute and return the distance of this shape (i.e. its reference position) from the origin.

• A method that creates a “resized” version of this shape and returns it.

• A method that compares two shapes based on their area and returns the result.

Note that all these operations make sense for both shapes, even though the way you would implement them would be different for each (e.g. computing the area of a circle requires different data and math than that for a rectangle.}

Java allows us a way to create a “specification” for the common operations that many classes are supposed to have. This is called a Java interface. Interfaces are similar to classes, except they contain only method signatures and no fields. Thus they are purely a list of operations.

Similar to classes, interfaces are also written one in a file.

3.2.2 Circle and Rectangle classes

Having written this interface, we can now write classes that implement it. We can write the Circle class as:

When a class implements an interface, it is required to implement all the methods specified in it. Thus the above code will not compile, but it will when we add definitions for all the methods in the Shape interface.

Similarly the Rectangle class can be written as:

This design can be expressed in a class diagram as follows:

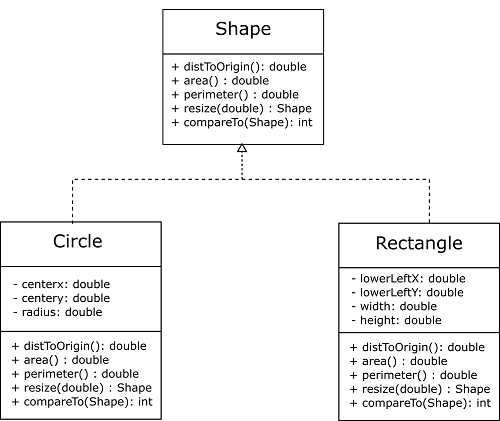
The dashed lines and the hollow triangle denote “implements”.

3.2.3 Fields

How can we represent the a circle with a position? Its position is denoted by the center (x,y) and its size is denoted by a radius. Using the double data type will allow us most flexibility.

A rectangle has a width and height. We choose the location of its lower left corner to be its position.

3.2.4 Constructors

We can write a simple constructor that initializes the center and radius of this circle to the values passed to it.

Sometimes for convenience we would like to create a circle with just the radius. We want the circle to have a default center of (0,0). We can offer this option to any user of this class by writing a second constructor for it.

We will define only one constructor for the Rectangle class:

3.2.5 The toString methods

How will we test whether the constructors are working correctly? We can written getter methods and use them in the tests. But we don’t yet have a good justification for methods that allow access. If we are going to test we can do so by writing toString methods that returns a string that represents the shape and test against it.

We introduce the use of a new method: String.format. This method is useful when a string of a particular format must be created. In this case we would like to print all our decimal numbers with exactly 3 numbers after the decimal point. We want Java to add trailing zeroes to fulfill this requirement if needed. Read more about this method in the documentation.

There is no standard format expected for the toString method. In this case we choose a format and made sure our tests are expecting the same format.

3.2.6 Tests

For now here are tests that verify that the two constructors for Circle and one constructor for Rectangle work as expected. They use the toString methods of these two classes.

If we wanted circle1 to be set to a Rectangle object we could! Thus circle1 can change its form at will. This concept is called polymorphism and is an important principle of OO. The advantage in this case, is that we can define variables that can be used for multiple (related) types of objects if need be. This is handy if we write some code and later decide that we want it to work with other, related classes.

Look at the line that declares variables for the various shapes. Normally we would have made all the variables for Circle objects to be of type Circle, and those for Rectangle objects to be Rectangle. However an interface can also be used as a type for an variable. What does this mean?

An variable whose type is an interface can be used for objects of any class that implements that interface. In other words the variable circle1 can be set to a Circle object, as well as a Rectangle object! This further underscores the idea that Circle and Rectangle are both related, in that they are both types of shapes. This is what union data type means: a Shape is either a Circle or a Rectangle (or any other shape that we choose to write like this).

3.2.7 Computing the area

In Java the methods that deal with each type of object are defined within the corresponding class definitions for those objects. So the area method that computes the area of a circle is defined in the Circle class, and the area method that computes the area of a rectangle is defined in the Rectangle class.

Remember again the difference in OO design: we are saying “circle/rectangle: compute your area”

Accordingly the area methods would be implemented as follows:

• We need to know the value of the mathematical constant $\pi$. This is provided by the Math class.

• The @Override is an annotation that means that this method was taken originally from something that this class implements.

• Normally you should write comments in the interface. If those comments completely describe what an implementing class is doing, there is no need to copy the comments over. Otherwise, write comments above this method.

The tests for these methods are:

3.2.8 Dynamic dispatch

It may be a bit surprising that the above test passes. Java called the area() method of the Circle class when we said assertEquals(Math.PI*25,circle1.area(),0.001); but called the area() method of the Rectangle class when we said assertEquals(5,rect1.area(),0.001);, even though the types of circle1 and rect1 are the same: Shape. Indeed by looking at just those lines and even the types of those variables, even we cannot tell where it should go!

If we now look at the context we see that circle1 is set to a Circle object and rect1 was set to a Rectangle object (this was done in setup()). Thus we expect those method calls to work the way they do. But how does Java know?

Python supports similar behavior, but takes it one step further. As Python does not require you to declare a type for a variable, it has no way of determining whether a function called on an object actually makes sense for that object. It takes a very liberal view: if the function being called exists in the object, then calling it should work (irrespective of whether it makes sense in the context or not). For example, consider if write a Person class and attempted to call a function “getAuthor” on a Person object. Although “getting the author of a person” makes no sense, calling this in Python is possible if the Person class actually has a function named “getAuthor”. This implies that Python believes that an object is defined completely and only in terms of its behavior. In other words, “if it looks like a duck, and it quacks like a duck, then (for all intents and purposes) it is a duck”. This analogy is quite literal, as Python terms this behavior duck typing. Duck typing is implemented in Python using a mechanism very similar to dynamic dispatch.

The process of matching a method call to a method body is called binding or dispatch. Java can do this in one of two ways. One way would be to bind when it is reading your code to compile it (i.e. statically). The other way would be to wait until you run the program, and then bind only when it must execute that line (i.e. dynamically). Java chooses the latter option, and is called dynamic dispatch.

We see above an advantage of this: we can write the area calculations for each shape in its own class, and then Java will figure out where to go depending on which object it is working with! The code looks clean.

Dynamic dispatch is convenient to distribute functionality in this way across union types. Whenever you are working with union types and feel the need to check what type you have: stop and try to use dynamic dispatch to eliminate that checking.

Consider another piece of magic thanks to dynamic dispatch: we can now reassign objects to variables in the setup method (as all variables are of type Shape) and the testArea() method, without changing any of its code, will now change its behavior accordingly!

Do Now!

Implement and test the perimeter method similarly.

3.2.9 Computing distance to origin

The distance to origin for a shape is the distance of the center of the circle to the origin, and the distance of the lower left corner to the origin for the rectangle. Accordingly, we can write these two methods as follows:

We observe that these methods are almost identical: both involve finding the distance of a point from the origin. Is there a way to avoid this code replication?

We observe that the computation requires only the knowledge of a point’s x and y coordinates. What if we represent a point as a class instead of two numbers inside these classes? We can then move to the point class the computation of its distance from the origin. The class diagram can be reworked as follows:

The arrows from Circle and Rectangle to Point2D are associations: read them as Circle has a Point, Rectangle has a Point.

Accordingly we create a Point2D class:

and then rewrite the Circle and Rectangle classes as:

Let us examine the salient features of this re-design:

1. Code replication is avoided: the math to compute the distance of a point to the origin is now only in the Point2D class. In general whenever you see code being replicated, try to redesign to avoid this.

2. Other than the Point2D class, no other class contains any code relevant to a point. We can use the Point2D class anywhere we need a point.

3. Because the shape classes do not contain any point-manipulation code directly in them, it is now easier to change to an alternative representation of a point. As an example, imagine representing a 2D point using the polar coordinate system rather than the Cartesian coordinate system. In order to do this, we would simply write a Polar2D class, put all the relevant operations in it and then have Circle and Rectangle simply store an object of Polar2D, nothing else!

4. We did not change the interface Shape or the constructors of the Circle and Rectangle classes. Due to this, our tests remain unchanged. In other words we redistributed code within the shape classes, without forcing the client code to change. This “internal changing” is referred to as code refactoring. The advantage is obvious: the maker of a class can change its implementation at any time without affecting those who are using the class. Note that this is possible only because we ensured that the list of public methods of our classes did not change in any way.

3.2.10 Resizing the shape

Look at the proposed method signature for resize in the Shape interface.

Why is this method returning a Shape object? We want the result of a resized circle to be a Circle object, and a resized rectangle to be a Rectangle object. Having a return type that can capture both (and all) possibilities makes this happen. However individual implementations of this method must ensure that the same kind of shape is returned.

We can see how a Circle or a Rectangle object can be returned when the return type is a Shape. This is not unlike what we saw in the tests, where a Shape variable could be set to Circle or Rectangle object.

We can test this method by verifying that different resizes work for both types of shapes.

Do Now!

What should happen if a negative number is passed as the resize factor? What will actually happen?

3.2.11 Comparing two objects

Look at the proposed method signature for compareTo in the Shape interface.

This comparison is based solely on areas, which we can compute for any shape by calling its area() method. Thus the implementations of this method would be:

They are identical! This is not surprisingly, since the comparison can be done by using methods in the interface (area()).

Do Now!

Write tests for the compareTo method.

Look at the way we specified the intended behavior of compareTo method in the Shape interface. This specification of what it will return in which situation is not accidental. This is the “standard” way of writing a method that compares two objects, and there is a Java interface written for this purpose: the Comparable interface. Thus whenever we wish to make two objects of our class comparable we can use this interface instead of defining explicitly what the compareTo method does. In our case, we make Shape borrow from the Comparable interface, as follows:

Comparable<Shape> means we wish to write a method whose signature is int compareTo(Shape other). Thus, whatever you specify in the Comparable interface becomes the type of the parameter to the resulting compareTo method.

3.2.12 Avoid code replication: Abstraction

The Shape interface captured the common operations for all shapes. However when we implemented the interface in the Circle and Rectangle classes we noticed that there are other common things: the existence of a reference point for each type of shape, the implementation of the compareTo method is the same for all shapes, etc. This resulted in code replication (compareTo was written twice although the code was identical, the reference point is defined in each shape and the distToOrigin method is defined separately even though they both are doing the same thing). It would be better if we avoid typing the same code in different placecs. Abstraction allows us to do this.

What we need is a place where we can put everything that is common to all shapes, so that individual shapes can simply get it from there. Interfaces only allow method signatures: we need something that can store common method bodies and fields. An abstract class allows us to do this.

AbstractShape implements Shape, and Circle and Rectangle extend AbstractShape. The AbstractShape stores the reference point and implements the compareTo and distToOrigin methods. It leaves some of the methods that it got from Shape for the actual shapes to implement. Thus the methods area(), perimeter() and resize(double) are specified in AbstractShape but not implemented there: these are called abstract methods. Because the AbstractShape class is incomplete it cannot be instantiated (i.e. one cannot create objects of that type).

Circle and Rectangle extend AbstractShape. This is an example of inheritance: one of the main principles of OO. Inheritance allows one class to inherit fields and methods of another class, and allows it to redefine inherited methods if necessary. The class that is being inherited from is often called the Base class, while classes that inherit from it are often called Derived classes. Inheritance is complete: a derived class inherits everything from its base class (it cannot pick and choose). Thus inheritance is appropriate only when a new class is everything an old class is, plus more or with slight modifications.

The effect of using inheritance in this example is that all common functionality can be put once in the abstract class, so that concrete shapes define only what is unique for them. This avoids code replication as desired, and further underscores the common aspects of shapes. Thus it is a coding and design win-win.

Notice another curious phenomenon: none of our tests changed! We redesigned our shape classes internally, without letting any clients be aware of them! This is another example of code refactoring, and is a necessary part of code development. Note that this was possible only because we defined an interface, and stuck to it while changing implementation details. This is another benefit of starting with an interface, and writing all client code using only interface names.

3.2.12.1 Coding details

• The resize methods need to access the reference point, which is now in AbstractShape and is private. Therefore we make it protected. A protected field or method can be directly accessed or called from a descendant class, but from nowhere else. Thus it is a special access modifier relevant only to inheritance, and is a compromise between private and public.

• Since the reference point is in the AbstractShape class, it makes sense that it be initialized in its constructor. But how does one call its constructor from the constructors of Circle and Rectangle constructors? We do this by using super(Point2D). super refers to the parent, similar to how this refers to itself. One can call a method defined in the base class as super.methodname(...). Similarly we can call the base constructor from the derived constructor by directly saying super(...). Any such call to the base constructor must be the first line inside the derived constructor.

3.2.12.2 Other sightings of inheritance

Given a situation is it better to use interfaces or abstract classes with inheritance? The answer is: both wherever appropriate! Interfaces allows us to write method signatures, and force any implementing classes to define those methods. Classes allows us to write fields and method bodies which derived classes can inherit. Abstract classes allow a happy medium: define some methods but not all. The recommendation is to start with an interface, then implement it and abstract common functionalities to an abstract class.

Inheritance is popular in many other situations. As said before, it is appropriate to use inheritance when a new class is everything that an old class, plus something else or with modifications. For example let us imagine we want to create a new shape, Square. We could define a new class that extends AbstractShape. But we realize that a square is just a rectangle with an additional constraint, its width is equal to its height. Note the sentence: a square is a rectangle. A hint for using inheritance is when you can frame a sentence relating the two classes with an is-a relationship. Thus we can write public class Square extends Rectangle. Inheritance need not be used only with abstract classes, as this example shows.

We have been wondering how Java can assume that every class we write will have a toString method. Now we can see how. Every class written in Java implicitly inherits from an existing class called Object. This class provides default implementations of many methods, including toString(). Because every class we write extends Object it gets those methods. If we wish to change the default method, we write a method whose signature exactly matches that of the inherited method. This is called method overriding, and explains the @Override tag when we define a toString method in one of our classes.

Java allows a class to extend at most one class: this is called single inheritance. Thus Circle extends AbstractShape, which implicitly extends Object. Thus Circle inherits all the methods defined in AbstractShape as well as Object.