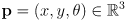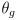Here is one way to modify the above algorithm so that it does not require decrease-key, and so that it does not mutate the sort key of any object that has already been added to the priority queue:
init empty priority queue Q of (vertex, dist) pairs sorted by increasing dist
# the dist part of each pair is immutable; more than one pair can be created for a single vertex
for each vertex v set v.visited = false, v.dist = infinity
set goal.dist = 0
add make-pair(goal, 0) to Q
while Q not empty # O(E) since inner loop adds a pair for every edge
(v, d) = pop Q # O(log E) with binary heap (Java PriorityQueue)
if not v.visited
set v.visited = true
# this inner loop iterates a *total* of O(E) times
for each neighbor vertex n of v with n.visited = false and n.dist > (v.dist + dist(v,n))
set n.next = v, n.dist = v.dist + dist(v,n)
add make-pair(n, n.dist) to Q # O(log E) with binary heap (Java PriorityQueue)