- distance to the object is thus
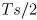 where
where
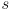 is the speed of sound in air
is the speed of sound in air - usually high-frequency sound is used to minimize annoyance, but there is still typically audible clicking at the pulse rate
- multiple sonars operating near each other usually need to be sequenced to minimize interference
- environmental sound and unwanted reflections can also cause problems
- an IR emitter sends a narrow focused beam out perpendicular to the sensor
- let
 be the distance from the sensor to an object in the environment
be the distance from the sensor to an object in the environment - some of the reflected light is collected by a lens with focal length
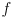 adjacent to the emitter at a fixed baseline distance
adjacent to the emitter at a fixed baseline distance
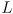
- the focused light its a position sensitive device (PSD) which reports its horizontal location as
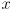
- by similar triangles,
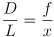
- thus
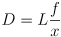
- diagram TBD
- the original concept of a laser scanner is based on time-of-flight of a laser light pulse
- in practice, many commercial implementations do not measure time of flight (which would require expensive very high speed electronics), but use approaches based on different types of interferometry
- for example, the emitted light could be amplitude modulated at e.g.
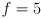 MHz, yeilding a wavelength of
MHz, yeilding a wavelength of
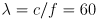 m where
m where
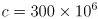 m/s is the speed of light in air
m/s is the speed of light in air - the phase difference
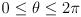 between the emitted and returned light is proportional to the distance
between the emitted and returned light is proportional to the distance
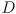 to the object:
to the object:
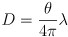
- diagram TBD
- note that aliasing will occur for
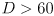 m, but in practice the returned beam will be significantly dimmed due to attenuation at some distance anyway
m, but in practice the returned beam will be significantly dimmed due to attenuation at some distance anyway - the beam is “scanned” across the scene by a spinning mirror, typically returning multiple range measurements in an angular band around the sensor
- a laser is used here mainly because it is easier to form a high-intensity tightly collimated (low-dispersion) beam which does not fan out very much over distance
- the high frequency stability of a laser can also allow narrow band-pass filtering of the returned light, to minimize interference from other light sources