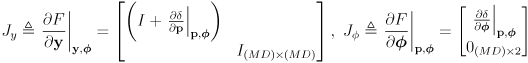Review of EKF Localization
- recall our approach from L15 for EKF localization of the robot pose
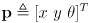 and its uncertainty represented as a
and its uncertainty represented as a
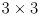 covariance matrix
covariance matrix
- the prediction phase is based on differential drive odometry given the incremental left and right wheel rotations
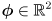 and corresponding
and corresponding
 covariance matrix
covariance matrix
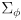 :
:
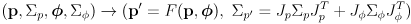 (1)
(1)
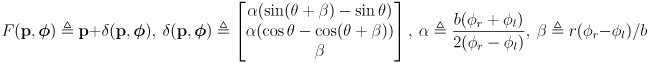
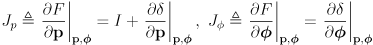
where
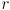 is the wheel radius and
is the wheel radius and
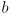 is the robot baseline
is the robot baseline
- the correction phase uses sensor data
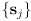 and its uncertainty
and its uncertainty
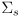 to detect features which may correspond to map landmarks
to detect features which may correspond to map landmarks
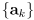 using a sensor modeled as a set of functions
using a sensor modeled as a set of functions
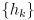 :
:
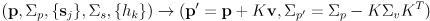 (2)
(2)
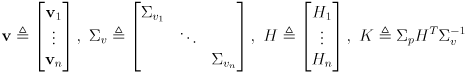
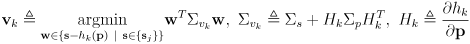
where
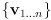 are the innovations which passed correspondence gating
are the innovations which passed correspondence gating
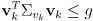 for a threshold
for a threshold
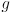 ,
,
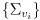 are the corresponding covariance matrices, and
are the corresponding covariance matrices, and
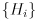 are the corresponding measurement model Jacobians
are the corresponding measurement model Jacobians
SLAM
- the localization problem is limited to estimating the robot pose, and assumes a map is known
- in the above formulation the map data
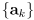 is embedded in the sensor models
is embedded in the sensor models
- where did the map come from?
- it must be built beforehand somehow
- in some cases it is manually developed
- in other cases it may be possible to use e.g. architectural floorplans to at least partially automate
- a very interesting generalization is to build the map from scratch as the robot moves
- this is called simultaneous localization and mapping (SLAM)
- because no map is required a-priori, a practical SLAM system could help enable significant autonomy
- this problem has been heavily studied over the last several decades in robotics research
- there are now a number of reasonably good solutions which can be applied in different settings
- e.g. a diff drive robot like ours operating on flat ground
- for underwater or aerial robots that move with 6 degrees of freedom
- using a laser rangefinder as the primary exteroceptive sensor
- using monocular or stereo vision
- etc.
- open software implementations for many SLAM algorithms have been posted on http://www.openslam.org
EKF SLAM
- one of the first and most well-studied approaches to SLAM is an extension of EKF localization
- the main idea is to generalize the EKF state to include not only the robot pose
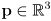 but also the entire map
but also the entire map
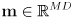 where
where
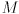 is the number of landmarks and
is the number of landmarks and
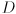 is the number of parameters stored for each landmark
is the number of parameters stored for each landmark
- the prediction phase is basically same as (1) but extended for the joint state
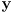 made by stacking the pose
made by stacking the pose
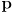 on top of the map
on top of the map

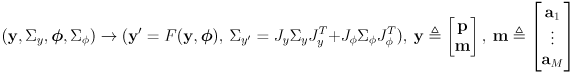 (3)
(3)
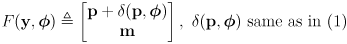
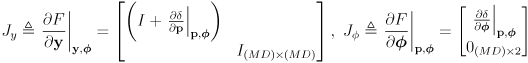
- the correction phase is based on (2) but
- the sensor models
 are a function of the full joint state
are a function of the full joint state
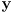 including the map and in particular the current estimate for landmark
including the map and in particular the current estimate for landmark
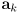 , not just the robot pose
, not just the robot pose
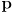
- the state vector
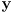 and its covariance matrix
and its covariance matrix
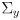 are potentially grown to add
are potentially grown to add
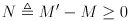 new landmarks
new landmarks
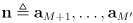 to the map:
to the map:
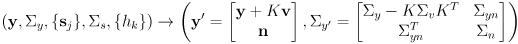 (4)
(4)
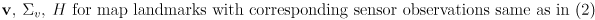
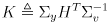
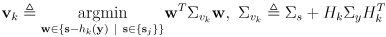
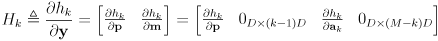
-
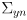 is a
is a
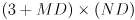 matrix of cross-covariances of the new landmarks with the old pose and landmarks
matrix of cross-covariances of the new landmarks with the old pose and landmarks
- in many implementations
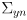 is all zero, but it could be used to model any initially estimated cross-covariance related to the new landmarks
is all zero, but it could be used to model any initially estimated cross-covariance related to the new landmarks
-
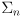 is an
is an
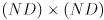 matrix
matrix
- the
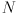
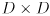 submatrices on its diagonal are the covariances of the new landmarks representing their initial uncertainties
submatrices on its diagonal are the covariances of the new landmarks representing their initial uncertainties
- these could be initialized if an estimate of the initial landmark uncertainties is available, though in a basic implementation they could be zero as well
- the off-diagonal submatrices above the diagonal are cross-covariances of each new landmark to the other new landmarks
- once more, they could be used to model initial cross-covariance but are often just set to zero
- the off-diagonal submatrices below the diagonal are just a mirror images of those above the diagonal
- where do the new landmarks come from?
- this is highly application-dependent
- in some cases a single sensor reading can give all necessary information for a landmark
- this includes the case we have studied with point landmarks with sensed range and bearing
- then one strategy is to consider sensor observations which did not pass any correspondence gating to be new landmarks
- however, in other cases, such as a range-only sensor and point landmarks, multiple sensor readings need to be combined in order to fully define a landmark
- also, to improve map quality, it may be helpful to only add new landmarks after they have been confirmed by multiple redundant sensor readings
-
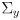 can be understood by considering it in blocks
can be understood by considering it in blocks
- the
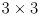 block at its upper left is a covariance matrix representing the current uncertainty in the robot pose
block at its upper left is a covariance matrix representing the current uncertainty in the robot pose
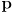
- the
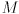
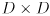 remaining blocks on its diagonal are covariance matrices representing the uncertainty of each of the landmarks
remaining blocks on its diagonal are covariance matrices representing the uncertainty of each of the landmarks
- the
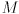
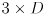 remaining blocks in its top row are the cross-covariances of the pose with each landmark
remaining blocks in its top row are the cross-covariances of the pose with each landmark
- the
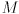
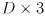 remaining blocks in the first column are mirrors of these
remaining blocks in the first column are mirrors of these
- the remaining set of
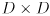 blocks above the diagonal are the cross-covariances of each landmark with the others, and these are also mirrored below the diagonal
blocks above the diagonal are the cross-covariances of each landmark with the others, and these are also mirrored below the diagonal
- when the various cross-covariance matrices are initialized to zero
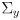 will have some sparsity
will have some sparsity
- but over time as more observations are made it will generally become dense
- in fact this indicates that the pose and landmarks become cross-correlated, which generally leads to an overall reduction of uncertainty
- but this also implies a major limitation of EKF SLAM: the memory storage and per-update computation time scale quadratically with the map size
- for this reason it is most appliccable to maps with roughly 1000 or fewer landmarks
- unfortunately mistakes in correspondence can cause major issues with EKF SLAM implementations in practice when there are relatively few landmarks, and in many applications more than 1000 would be preferred
- newer approaches have been developed which can overcome these issues
- understanding EKF SLAM is an important starting point
Other Approaches to SLAM
- graph-based SLAM represents the problem as an abstract graph
- the history of robot poses and the map landmarks are represented as vertices in an abstract graph
- edges represent constraints on their relative poses, either from odometry or sensing
- various algorithms are applied to relax the model, attempting to globally improve satisfaction of all the constraints by adjusting the poses
- the storage requirements of graph-based SLAM are usually linear in the size of the map, not quadratic as in EKF SLAM
- the running time depends on the optimization technique used
- some are fast but only optimize a subset of the graph related to the current robot pose
- others perform global optimization but are slower and may not run fast enough to be used on-line for large maps
- FastSLAM uses a particle filter to represent a sampling from the distribution of joint pose/map states
- the storage requirements of FastSLAM are linear in the size of the map, not quadratic as in EKF SLAM
- its update time complexity is logarithmic in the size of the map, so it can handle very large maps
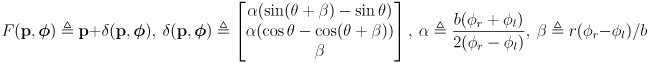
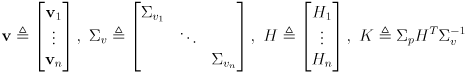
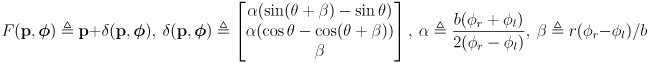
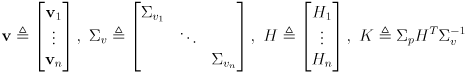
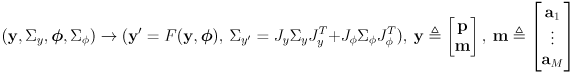 (3)
(3)