Contents
How TLAPS Works
Running the Proof Manager
Stopping a Proof
How the Toolbox Displays the Status of Proofs
The Status of Obligations
Logical Colors and Color Predicates
Interesting Obligations
Updating Proof Statuses
Finding Errors
Advanced Topics
Advanced Execution Preferences
The Launch Prover Command
User-Defined Color Predicates
TLAPS consists of a Proof Manager (PM) and various back-end provers. In TLA+, a proof of a theorem or proof step is either a leaf proof or a sequence of steps, each of which may have a proof. The PM translates a proof into a collection of obligations whose correctness implies the correctness of the proof. A proof's obligations include the obligations of each subproof. The PM calls one or more back-end provers to prove the obligations. It then displays with colors the proof status of of each theorem or proof step whose proof it has checked. The proof status of a step or theorem is determined by which of its proof's obligations the back-end provers succeeded in proving. The section titled How the Toolbox Displays the Status of Proofs explains how you can completely customize the colors and their significance.
To tell the PM to check the proof of a theorem or step,
place the cursor (not the mouse pointer) on that theorem
or step and execute the command Prove Step or Module.
You can do this either from the menu you obtain by right-clicking in
the module editor, or by typing Ctl+G Ctl+G.
If you execute this command when the cursor is not at a theorem or step,
the PM will check all proofs in the module.
The PM can be executed with various options.
You will probably want to use only the default options.
Some that you might want to change for regular use can be set with
prefences, as described in the
Advanced Execution Preferences subsection below.
Even more esoteric PM options can be invoked using the Launch Prover
command described below.
The PM remembers the outcome of the back-end provers' attempts to prove each obligation. If the PM finds that an obligation has already been proved, its default behavior is to accept it as true and not send it again to a back-end prover. Checking if an obligation has already been proved is fast, so there is no harm telling the PM to prove something it has already proved.
If something mysterious happens when running the PM and you think something has gone wrong, you can try looking at the TLAPM console, which you can display by using the TLA Proof Manager menu at the top of the Toolbox window. It shows the output that the PM sends to the Toolbox.
When executing the PM, you can stop an individual proof or the entire execution. As explained below, the Toolbox shows obligations that a prover has been trying to prove for a while. You can tell PM to stop proving that obligation by clicking on the Stop Proving button at the top of the obligation. You can stop the entire execution by clicking on the Cancel button of the Prover Launch dialog.
Note: If you check Always run in background on the Prover Launch dialog,
that dialog will stop popping up when you run the PM.
To get it back, go to File/Preferences/General and uncheck the
Always run in background preference.
The PM displays with colors the proof status of steps and theorems whose proofs it checks. The status of a step or theorem depends on the results of checking its proof obligations. For each back-end prover and each obligation, there are five possible statuses of the checking of that obligation by that prover:
OMITTEDwhich indicates that the user has explicitly chosen to omit the proof. In this case, the step is considered to have a dummy obligation whose status is omitted. TLA+ also allows incomplete proofs in which some proofs are missing, usually because they have yet to be written. In this case, the step is considered to have a dummy obligation whose status is missing.
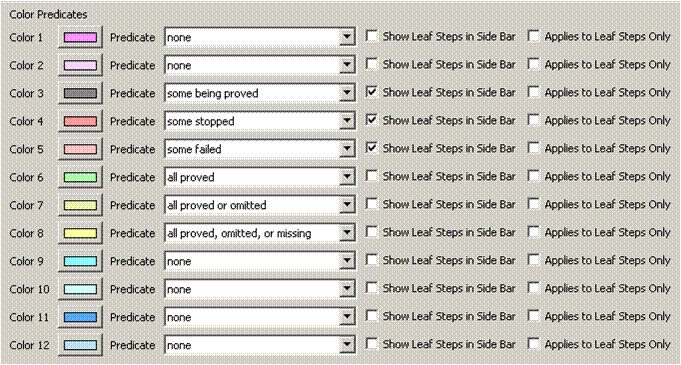
A step is colored with one of 12 logical colors, numbered from 1 through 12, or else is uncolored. Each logical color has an associated color predicate which is either true or false, depending on the statuses of the step's proof obligations. The step is colored with the lowest-numbered color whose color predicate is true, or is left uncolored if all the color predicates are false. Here is a picture of the main TLAPS preference page showing the 12 colors and their default color predicates:

The predicate for color 4 is true if and only if the user stopped a back-end prover while it was proving one of the proof's obligations. The predicate for color 7 is true if and only if every obligation of the proof was either proved by some back-end prover or is an omitted obligation (a dummy obligation with status omitted). The predicate none is never true. The menu allows you to set a color's predicate to one of a number of predefined predicates or to one of six user-defined predicates named user-defined A, ... , user-defined F. In addition to the predefined color predicates, you can also choose any of six user-defined predicates. The subsection User-Defined Color Predicates below explains how to define those color predicates.
A color's predicate can be set to be true only for leaf steps (or theorems)--ones with no substeps--by checking the Applies to Leaf Steps Only field. The Show Leaf Steps in Side Bar field indicates if leaf steps colored with that logical color should be highlighted by a mark on the right-hand side of the module editor, next to the appropriate point in the vertical scroll bar. (These two choices are independent of one another.)
The picture shows the default physical colors corresponding to the logical colors. You can change a color by clicking on the appropriate colored button on the preference page.
When checking a proof, the Toolbox displays interesting obligations in a separate window. Here is what can make an obligation interesting:
The obligation is a TLA+ representation of the exact mathematical fact
that the back-end prover is required to prove.
The back-end prover sees nothing except what the displayed obligation
contains.
For example, suppose your specification defines Two by
Two == 2A back-end prover will have no way of proving the obligation
1+1 = Twobecause it has no idea what
Two means.
A proof that generates this obligation is incorrect because it fails
to indicate that the definition of Two must be used.
When the proof is finished, either because there are no more obligations to be checked or you have canceled the command from the Prover Launch dialog, the colors shown in the module editor reflect the correct status of the proof(s) that were checked. Making a change to the module can change the obligations the PM generates for a proof, changing the proof status of steps. For example, changing the definition of a symbol is likely to change the obligations for the proof of any formula containing that symbol. A step's color is not changed to reflect changes to the module. You can edit the module while running a proof, but the proof is performed on the module as it was when TLAPS was launched.
Calling the PM to check the proof of a step (or a proof containing that step) causes the step's color to be updated appropriately. (Remember that this entails no further proving if the proof's obligations have not changed.) You can also use the Check Status of Step or Module command (Ctl+G Ctl+T) to update proof step colors. This works just like the Prove Step or Module command, except it does not do any proving. It just computes the indicated steps' proof statuses based on the status of its obligations obtained from proofs it has already attempted. (It too displays interesting obligations.)
You can edit the module while the Check Status command is running. You can therefore issue the command to update the status of all the module's proofs and let it run while you continue editing a proof. A step's color will be determined by the module's contents when the command was issued.
There are some errors in a proof that are detected by the PM before sending a proof, or a proof obligation,
to the back-end provers.
These can be actual mistakes in the proof--for example, using a TAKE step when the
current goal is not a universally quantified formula.
They can also be TLA+ features not supported by TLAPS, such as quantification over tuples, as in
\A <<x, y, z>> \in S : ... .
Currently, the Toolbox does not always properly report errors found by the PM. When you encounter a problem whose cause you can't figure out, try looking at the TLAPS Console Log, which can be displayed from the TLA Proof Manager menu.
--solver
option.)
Ctl+G Ctl+P) can be
used to execute the PM with options that cannot be specified by using
the ordinary Prove Step Or Module command with appropriate preference
settings.
Issuing this command raises a dialog with which you choose the PM options
from the following selections.
The Additional Preferences subpage of the main TLAPS preference page allows you to define color predicates. You can define almost any color predicate you might want. Here is a complete explanation of how. Don't worry if you find the explanation hard to understand. The Toolbox won't let you enter an illegal definition, and you can experiment until you figure out how to write the definition you want.
At any time, an obligation has a state.
For the dummy obligation representing a missing proof or
the proof OMITTED,
its state
is either missing or omitted. An ordinary proof
obligation's state consists of a status for each prover.
We consider there to be three provers:
untried, proving,
proved, failed, stopped untried, proving, proved, failed, stopped none, trivial (proving, failed, none),
where the value of the ith element
is the obligation's proof status for the ith prover.
A color predicate is specified by two things:
A color predicate is specified by a string with the following syntax
<color-predicate> ::= ["every" | "some"] <state-set>*
<state-set> ::= "missing" | "omitted"
| "(" <statuses> "," <statuses> "," <statuses> ")"
<statuses> ::= <status>* | "-" <status>+
Each <state-set> specifies a set of states, and a
sequence of <state-set>s specifies their union.
The <state-set>s "missing" and "omitted"
specify the obvious singleton sets of dummy-obligation states.
A <statuses> specifies a set of possible prover statuses
as a list, where "-", means all statuses
except and the empty list means all possible statuses.
A triple of sequences of statuses specifies the set of all states in
which the proof status of the ith prover is one of
the statuses in the ith component of the
triple.
An empty sequence of statuses is an abbreviation for all possible
statuses. For example, the <state-set>
(proving proved, untried, )is the set of all obligation states in which Isabelle's proof status is either
proving or proved, the Other
prover's status is untried, and the PM's prover status is either
none or trivial.
We can write a color predicate that is always true as: every missing omitted ( , , )The color predicate
someis false for every proof. The predicate
every omitted (proved, , ) (, proved, ) (, , trivial)is true iff every obligation is either omitted, is proved by Isabelle or the Other prover, or is found trivial by the PM. The predicate
some (failed, - proved, none) (- proved, failed, none)is true for a proof iff, for at least one of its obligations, either Isabelle's status is
failed and the Other prover's status
is not proved, or vice-versa, and the PM has not found it
to be trivial.