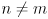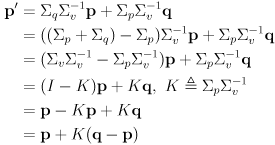Error Propagation
- the main topic of this lecture will be a more formal, but still quite practical, approach to localization than we covered in L8
- we are still assuming that there is a world map with known landmarks that the robot can potentially measure using an exteroceptive sensor like a camera or laser rangefinder
- this concerns the differential drive mobility subsystem (the wheels), but we start with a case study of our robot’s arm
- the idea will be to understand how small errors in the setting of the arm joint angles propagate to (hopefully) small errors in the gripper position
- the math we develop to do this will critically depend on the manipulator Jacobian which we introduced in L9
- later we will show that the mobility system in fact also has its own Jacobian(s), so our case study for the arm will translate to the wheels
- recall that we often command the arm joint angles
 maintaining the constraint
maintaining the constraint
- specifically, we slave the wrist joint
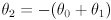 and only command the shoulder and elbow joints
and only command the shoulder and elbow joints
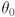 and
and
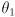
- in this way the gripper always remains horizontal and the arm forward kinematics reduces to
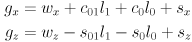 (1)
(1)
where
-
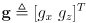 is the grip point in the vertical plane of robot frame
is the grip point in the vertical plane of robot frame
-
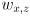 are constants giving the grip point in link 2 frame
are constants giving the grip point in link 2 frame
-
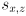 are constants giving the shoulder joint location in robot frame
are constants giving the shoulder joint location in robot frame
-
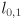 are the lengths of arm links 0 and 1
are the lengths of arm links 0 and 1
-
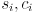 are
are
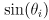 and
and
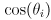
-
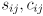 are
are
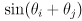 and
and
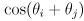
- equations (1) can be collected together into a single forward kinematic function for the arm:
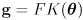 (2)
(2)
where
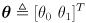
- this is a nonlinear function that transforms a point
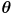 in joint space to a point
in joint space to a point
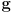 in task space
in task space
- in this example joint space and task space are both two-dimensional
- TBD diagram
- in the remainder of this analysis we will make no assumptions about the workings of the nonlinear function
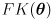 except that it is differentiable
except that it is differentiable
- this analysis can be applied to any differentiable function with an
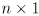 input vector and
input vector and
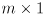 output vector, even for
output vector, even for
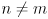
- say the arm is nominally set to joint angles
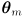 , but these settings have been perturbed by a small error
, but these settings have been perturbed by a small error
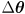 in joint space
in joint space
- what is the corresponding error
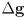 in task space?
in task space?
-
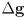 can be estimated by taking a local linear approximation of (2):
can be estimated by taking a local linear approximation of (2):
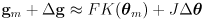 (3)
(3)
where
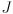 is the derivative of
is the derivative of
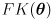 evaluated at
evaluated at
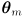 :
:
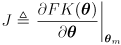
- this is the same equation we used in L9 as a basis for incremental numeric inverse kinematics
- but here we are using it for another purpose, specifically to estimate
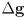 given
given
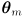 and
and
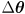
- subtract
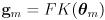 from both sides of (3) to get
from both sides of (3) to get
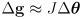 (4)
(4)
- the Jacobain
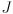 is a
is a
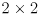 matrix in this example, or in general
matrix in this example, or in general
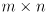 where task space is
where task space is
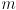 dimensional and joint space is
dimensional and joint space is
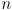 dimensional
dimensional
- in this example
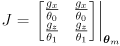
- remember
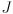 is not constant, it must be computed based on the current nominal joint angles
is not constant, it must be computed based on the current nominal joint angles
Gaussian Uncertainty Modeling
- why would the arm joint angles be perturbed?
- we measure them in the robot with potentiometers
- but these measurements are subject to some amount of error
- this is similar to measuring distance with a ruler
- if your ruler is marked in mm then you may be able to read it off to within, for example
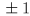 mm
mm
- or more generally within
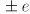 mm, where
mm, where
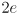 is an uncertainty interval
is an uncertainty interval
- let’s attempt to model the uncertainty in the arm’s joint angles with a similar approach using uncertainty intervals
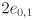 for the two joint angles
for the two joint angles
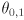
- we could represent this graphically by drawing an axis-aligned rectangle centered at the nominal joint angle setting
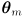 in joint space
in joint space
- but does this imply some kind of corresponding axis-aligned rectangle representing uncertainty in task space, centered on
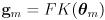 ?
?
- unfortunately it does not, but a related idea will work
- instead of using an axis-aligned rectangle, let’s model uncertainty using a possibly rotated ellipse centered at
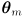
- it does turn out that in this model there is a corresponding uncertainty ellipse in task space centered at
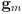
- we will see how to estimate this latter ellipse below by first-order propagation of uncertainty
- what does such an uncertainty ellipse mean, and how should we parameterize it?
- the generally accepted approach is based on Gaussian uncertainty modeling
- start by recalling the shape of a 1-dimensionial Gaussian distribution
- TBD diagram
- this curve is parameterized by two numbers:
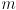 and
and
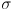
-
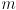 is the mean value of the Gaussian, i.e. the location of its peak
is the mean value of the Gaussian, i.e. the location of its peak
- if we had to give a single best estimate for the measured quantity, it would be
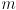
- the standard deviation
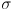 defines the spread of the Gaussian
defines the spread of the Gaussian
-
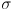 is a compact way to quantify our level of certainty that the actual value is near
is a compact way to quantify our level of certainty that the actual value is near
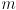
- sometimes we use the notation
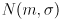 to refer to the Gaussian (aka normal) distribution with median
to refer to the Gaussian (aka normal) distribution with median
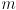 and standard deviation
and standard deviation
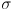
- the corresponding thing in 1D to an uncertainty ellipse is actually an uncertainty interval
- think of “cutting” the Gaussian curve with a horizontal line at some elevation
- the elevation is inversely related to a desired confidence level
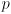 (a percentage that we can select, for example
(a percentage that we can select, for example
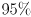 ) so that the perturbed value of the measurement is expected to be within the resulting interval with that level of confidence
) so that the perturbed value of the measurement is expected to be within the resulting interval with that level of confidence
- higher values of
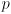 correspond to cutting at lower elevations, making larger intervals
correspond to cutting at lower elevations, making larger intervals
- because the Gaussian has infinite tails,
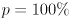 implies an infinite interval
implies an infinite interval
- for
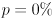 the interval degenerates to a single point at
the interval degenerates to a single point at
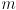
- this can be made precise with a few equations, but we don’t really need that level of detail here
- now extend this approach to two dimensions with mean
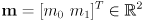 and first with independent uncertainties
and first with independent uncertainties
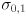
- the 2D Gaussian distribution looks like a mountain
- TBD diagram
- cutting it with a vertical plane along each axis gives 1D Gaussians
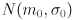 and
and
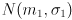
- TBD diagram
- cutting it with a horizontal plane at an elevation inversely related to a confidence level
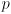 gives an axis aligned (i.e. un-rotated) uncertainty ellipse
gives an axis aligned (i.e. un-rotated) uncertainty ellipse
- TBD diagram
- it will be useful to collect the independent uncertainties
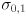 into a single
into a single
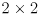 diagonal covariance matrix
diagonal covariance matrix
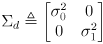 (5)
(5)
-
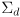 encapsulates all necessary information about the relative uncertainties in each axis
encapsulates all necessary information about the relative uncertainties in each axis
- when a confidence level
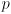 is additionally given,
is additionally given,
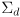 can be used to calculate the ellipse major and minor diameters
can be used to calculate the ellipse major and minor diameters
- this can be made precise with a few equations, but we don’t really need that level of detail here
-
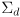 is usually positive definite because there is usually some non-zero uncertainty in each axis, i.e.
is usually positive definite because there is usually some non-zero uncertainty in each axis, i.e.
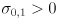
- to allow rotated ellipses, introduce a local frame with origin at the center of the ellipse and with axes in the directions of the ellipse major and minor diameters (which are mutually perpendicular by definition)
- TBD diagram
- a
 basis
basis
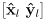 for this local frame is given by the familar 2D rotation matrix
for this local frame is given by the familar 2D rotation matrix
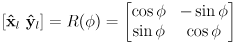
where
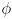 is the CCW rotation from the global
is the CCW rotation from the global
 axis to
axis to
- then a more general covariance matrix
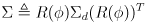 (6)
(6)
can be defined where
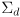 is the diagonal covariance matrix from (5)
is the diagonal covariance matrix from (5)
- read (6) from right to left as
- rotate from global to local frame
- model uncertainty independently along the local frame axes
- rotate back to global frame
- in that way, the general covariance matrix
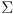 encapsulates both the rotation of the ellipse
encapsulates both the rotation of the ellipse
 and the relative lengths of the ellipse diameters
and the relative lengths of the ellipse diameters
- for particular ellipse diameters a confidence level
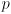 is must also be specified, as usual
is must also be specified, as usual
- by construction
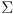 is symmetric and (usually) positive definite
is symmetric and (usually) positive definite
- all of this generalizes to higher dimensions
- summing up, we can define a Gaussian (aka normal) distribution in
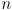 dimensions as
dimensions as
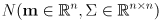
-
 is the nominal (mean) value of the distribution
is the nominal (mean) value of the distribution
-
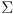 is a symmetric and (usually) positive definite matrix that defines the orientation of uncertainty ellipses (ellipsoids for
is a symmetric and (usually) positive definite matrix that defines the orientation of uncertainty ellipses (ellipsoids for
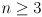 ) for the distribution, as well as the ratios of their principal diameters
) for the distribution, as well as the ratios of their principal diameters
- to actually draw a particular uncertainty ellipse (or ellipsoid, or interval for
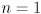 ) you also need to supply a confidence level
) you also need to supply a confidence level
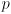 , which combined with
, which combined with
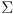 gives the specific diameters of that ellipse/ellipsoid/interval
gives the specific diameters of that ellipse/ellipsoid/interval
Propagation of Uncertainty
- now we are ready to see how a nominal setting of the robot arm joint angles
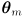 and a corresponding covariance matrix
and a corresponding covariance matrix
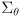 propagates to a nominal gripper position
propagates to a nominal gripper position
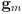 and its covariance matrix
and its covariance matrix
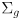
- TBD figure
- in fact, we have already done half of this in (2):
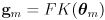 (7)
(7)
- the other half is based on (4):
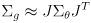 (8)
(8)
- to understand (7), think of the Jacobian
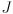 (and remember this is the particular
(and remember this is the particular
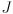 evaluated at
evaluated at
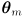 ) as a mapping from errors in joint space to errors in task space
) as a mapping from errors in joint space to errors in task space
- then read (7) from right to left (note the similarity to (6))
- transform from task to joint space
- apply the joint space uncertainty
- transform from joint space back to task space
- while (4) motivates the idea that
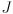 transforms errors from joint to task space, it is not necessarily obvious that
transforms errors from joint to task space, it is not necessarily obvious that
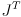 would do the opposite, and not, for example
would do the opposite, and not, for example
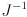 or a pseudoinverse of
or a pseudoinverse of
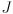 when it is not invertible
when it is not invertible
- we will not cover the proof, but in fact
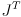 is the right thing here
is the right thing here
- equations (7) and (8) constitute first-order propagation of uncertainty
- they work for any general differentiable function
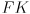
Differential Drive Odometry with Uncertainty
- in L3 we developed equations for incremental forward position kinematics, i.e. odometry, for the differential drive mobility system on our robot
- at each time step we calculate a new robot pose
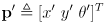 given the prior pose
given the prior pose
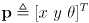 and the incremental wheel rotations
and the incremental wheel rotations
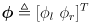 that occurred in this timestep:
that occurred in this timestep:
 (9)
(9)
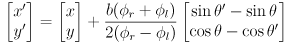 (10)
(10)
where
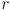 is the wheel radius and
is the wheel radius and
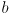 is the robot baseline (the distance between the wheels)
is the robot baseline (the distance between the wheels)
- equations (9) and (10) are another nonlinear but differentiable mapping
- here there are two inputs:
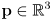 and
and
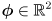
- and one output:
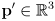
- because we will use
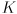 for a different purpose below, we will call this mapping simply
for a different purpose below, we will call this mapping simply
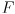 (instead of
(instead of
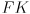 as we did for the arm):
as we did for the arm):
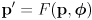 (11)
(11)
- equation (11) can be considered to have two Jacobians:
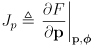 ,
,
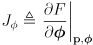 (
(
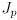 is
is
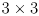 and
and
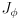 is
is
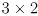 )
)
- for incremental odometry we repeatedly apply (11) to get a sequence of nominal robot poses

-
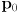 is the original pose when the robot was turned on or when odometry was most recently reset
is the original pose when the robot was turned on or when odometry was most recently reset
-
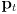 is the current pose
is the current pose
- now we can use first-order propagation of uncertainty to also maintain a sequence of
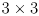 covariance matrices
covariance matrices
 modeling uncertainty in the pose at each step
modeling uncertainty in the pose at each step
- apply the uncertainty propagation (8) to
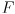 like this:
like this:
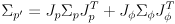 (12)
(12)
-
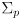 is the uncertainty of the prior pose
is the uncertainty of the prior pose
- in the typical case that we define the first robot pose
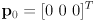 then
then
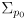 is all zeros (no initial uncertainty)
is all zeros (no initial uncertainty)
-
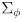 models the process uncertainty for the mobility system given that the wheel encoders reported an incremental wheel rotation of
models the process uncertainty for the mobility system given that the wheel encoders reported an incremental wheel rotation of
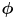
- it is a bit of an art to come up with a useful model for
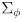
- one possibility is to make it a constant diagonal matrix
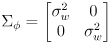
where
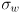 is a standard deviation modeling uncertainty in knowing the effective wheel rotation, which may vary from the actual wheel rotation due to slip between the wheel and the ground
is a standard deviation modeling uncertainty in knowing the effective wheel rotation, which may vary from the actual wheel rotation due to slip between the wheel and the ground
- another possibility is to make
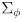 depend on
depend on
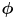 , for example
, for example
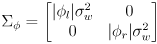
- this models the uncertainty for each wheel to be proportional to the amount it rotated
- in any case the parameters of the uncertainty model (such as
 ) may need to be determined by experiments
) may need to be determined by experiments
- or you could make a reasonable guess
- because (12) not only projects the prior pose uncertainty
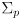 forward, but also adds on some additional uncertainty from
forward, but also adds on some additional uncertainty from
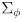 , the pose uncertainty will increase at each timestep
, the pose uncertainty will increase at each timestep
- this matches our intuition that the longer the robot operates “blindly” estimating its pose only with odometry, the more error will accumulate
- TBD figure
- if the robot has no additional exteroceptive sensors, this is arguably the best estimate of its position it can make
- but of course we can add sensors like cameras and laser scanners, and shortly we will see how to use them to attempt to periodically reduce pose uncertainty
- note that since
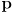 is three dimensional technically we would have to draw a 3D plot and show the robot’s trajectory in
is three dimensional technically we would have to draw a 3D plot and show the robot’s trajectory in
 state space
state space
- uncertainty at each step could be visualized as an ellipsoid in 3D
- but it is common to plot only the
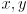 (position) part of the state
(position) part of the state
- the 2D error ellipse for the
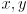 part of state
part of state
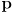 is described by the upper left
is described by the upper left
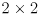 submatrix of the corresponding
submatrix of the corresponding
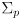
EKF Localization
- the incremental odometry update equations (11) and (12) can be considered the prediction phase of an extended Kalman filter (EKF)
- the original Kalman filter was designed only to apply to linear process functions
- the extended Kalman filter handles nonlinear but differentiable functions
 by taking locally linear approximations as we did in equation (3)
by taking locally linear approximations as we did in equation (3)
- this is approximation but it often works well in practice
- in general, a Kalman prediction transforms a prior state estimate
 and its uncertainty modeled as a covariance matrix
and its uncertainty modeled as a covariance matrix
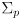 into a new state estimate
into a new state estimate
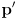 and its (generally larger, possibly equal, but never smaller) uncertainty
and its (generally larger, possibly equal, but never smaller) uncertainty
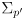 , accounting for a known differentiable process function
, accounting for a known differentiable process function
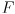 and process update
and process update
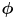 with uncertainty
with uncertainty
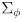 :
:
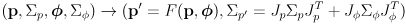 (13 Kalman prediction)
(13 Kalman prediction)
where
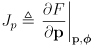 ,
,
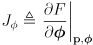
- the other phase in an EKF is called a correction phase
- for mobile robot localization with a known map, Kalman correction is the process by which the exteroceptive sensor(s) on the robot (camera, laser rangefinder, etc) are used to
- observe the environment
- look for features that might correspond to known landmarks in the map
- propose a particular correspondence between (some of) the observed features and known landmarks
- infer from these correspondences some information about the actual pose called the innovation
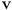 with uncertainty
with uncertainty
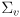
- use the innovation to reduce the pose uncertainty
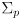 and to refine the nominal pose estimate
and to refine the nominal pose estimate
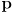
- these will be detailed below
- the EKF is a recursive filter in the sense that the only “memory” it keeps is the most recent state estimate
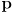 and its covariance
and its covariance
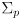
- each update makes a new
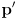 and
and
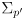 to replace the old ones
to replace the old ones
- in many applications every update has both a prediction phase and a correction phase
- but for mobile robot localization often there are many updates where only the prediction phase is applied, hence growing the pose uncertainty
- correction phases which reduce pose uncertainty are often applied at a lower frequency due to their computational cost, and in some cases to the limited speed and/or relatively high power consumption of exteroceptive sensors
- to develop the equations for Kalman correction, first consider a special case where we abstract away feature observation and correspondence, and assume that the “innovation” from the exteroceptive sensor is simply a full state estimate
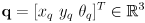 and its
and its
 uncertainty matrix
uncertainty matrix
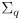
- here the innovation is
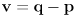 (14)
(14)
but in general this need not be the case because the data from sensing need not actually be a pose
- this special case could occur in practice if the robot has something like a GPS sensor to estimate
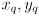 and something like a compass to estimate
and something like a compass to estimate
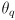
- if GPS were available you may wonder why we would need to do anything further
- in practice, GPS is not always available, particularly indoors
- also the resolution of GPS, at least for economical equipment, is on the order of meters
- and while GPS reports position in a geo-referenced coordinate frame, what may be more important to a robot is its position relative to nearby obstacles, and the transformation from a map of those obstacles to the geo-referenced frame may not be precisely known
- in this case the correction phase boils down to combining the prior pose estimate
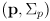 and the estimate
and the estimate
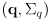 from sensing
from sensing
- the main idea is to make the refined nominal pose estimate
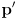 a weighted average of the prior estimate
a weighted average of the prior estimate
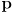 and the estimate from sensing
and the estimate from sensing
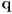 :
:
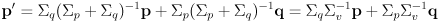 (15)
(15)
- where we have used the fact that the covariance of the innovation
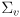 is
is
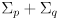 , which can be found by propagation of uncertainty on (14):
, which can be found by propagation of uncertainty on (14):
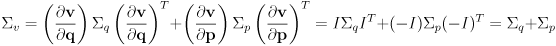 (16)
(16)
- equation (15) gives more weight to
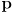 if the uncertainty for
if the uncertainty for
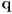 is high and vice-versa
is high and vice-versa
- to understand equation (15), consider a simplified case where the state is one-dimensional, i.e.
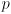 and
and
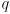 are just scalars
are just scalars
- then the covariance matrices reduce to just variances and (15) can be written like this:
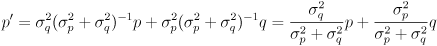 (17)
(17)
- equation (17) makes it a bit more clear that when the variance for
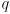 is high more weight is given to
is high more weight is given to
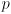 and vice-versa, but the same logic still holds for the multidimensional version in (15)
and vice-versa, but the same logic still holds for the multidimensional version in (15)
- it is typical to rearrange (15) like this
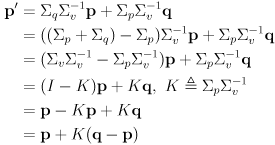
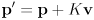 (18)
(18)
which is more explicitly recursive
-
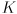 is called the Kalman gain
is called the Kalman gain
- the covariance of the refined estimate
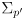 is found by yet another application uncertainty propagation, here on (18):
is found by yet another application uncertainty propagation, here on (18):
$\begin{aligned} {p’} &= () p ()^T
- () q ()^T \ &= (I-K)p(I-K)^T + KqK^T \ &= p-pKT-Kp+KpKT+KqK^T \ &= p-p(pv{-1})T-(pv{-1})p+ K(p+q)K^T \ &= p-pv{-T}pT-pv{-1}p+ KvK^T \ &= p-pv{-1}p-pv{-1}p+ (pv{-1})v(pv{-1})T \ &= p-2pv{-1}p+ pv{-1}vv{-1}p \ &= p-2pv{-1}p+ pv{-1}p \ &= p-pv{-1}p \ &= p-(pv{-1})v(v^{-1}p) \ \end{aligned}
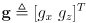 is the grip point in the vertical plane of robot frame
is the grip point in the vertical plane of robot frame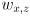 are constants giving the grip point in link 2 frame
are constants giving the grip point in link 2 frame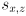 are constants giving the shoulder joint location in robot frame
are constants giving the shoulder joint location in robot frame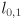 are the lengths of arm links 0 and 1
are the lengths of arm links 0 and 1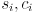 are
are
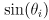 and
and
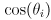
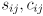 are
are
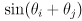 and
and
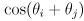
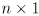 input vector and
input vector and
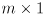 output vector, even for
output vector, even for