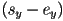Computer Graphics (CS 4300) 2010S: Lecture 4
Today
- HW2 and HW3 out
- loose ends (frame buffers & double buffering, signed distance from point to line)
- midpoint algorithm for rasterizing line segments
- line attributes
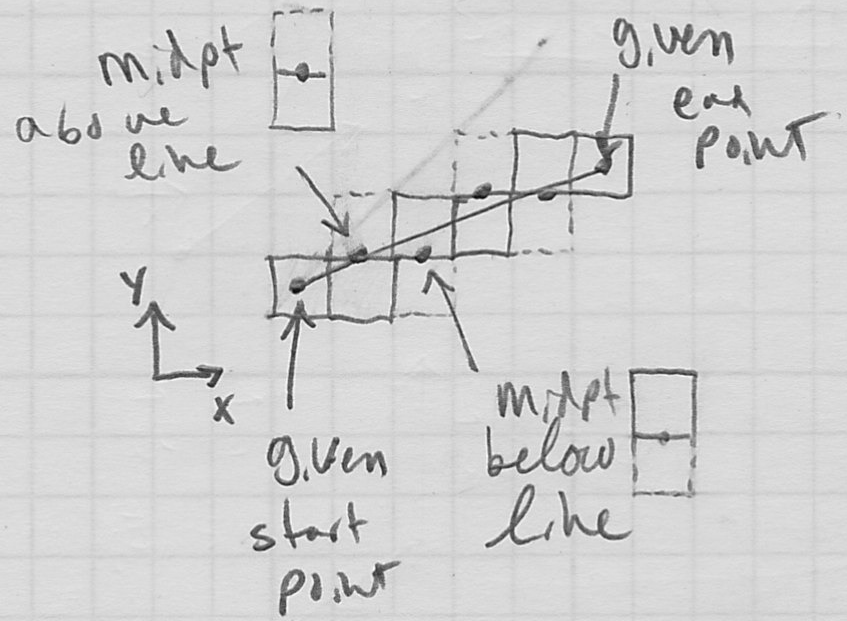
Midpoint Algorithm
- given a line segment, e.g. as start and end points
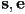 , how should we decide how to “turn on” pixels to display it?
, how should we decide how to “turn on” pixels to display it? - this is an example of rasterization: converting a description of geometry (or model) into an image
- we need an algorithm that will return a resonable set of pixels; one common method is called the midpoint algorithm
- first, observe that it is sufficient to only consider the case of a line in quadrant I with more run than rise, i.e. all coordinates positive and
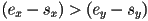 . Any other line can be handled by small tweaks to this case.
. Any other line can be handled by small tweaks to this case. - overall structure of the algorithm:
 (start at bottom)
(start at bottom)- for
 to
to 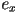 do (iterate from left to right)
do (iterate from left to right)- turn on pixel
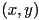 (we are now “on” a line pixel)
(we are now “on” a line pixel) - if condition then
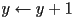 (need to move up)
(need to move up)
- The interesting part is condition. Idea: compute the midpoint
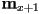 between the centers of the pixels at
between the centers of the pixels at 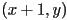 and
and  (i.e. the pixel immediately to the right and the one above it); if
(i.e. the pixel immediately to the right and the one above it); if 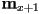 is below the ideal line connecting
is below the ideal line connecting 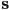 to
to 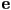 , then the pixel at
, then the pixel at  is closer to the line than
is closer to the line than 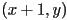 , so move up.
, so move up.
- computing the midpoint coordinates is actually trivial:
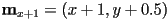
- but how to determine if
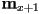 is above or below (or on) the line?
is above or below (or on) the line? - we have already seen one method: make a temporary vector from
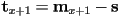 and take the cross product of it and the vector
and take the cross product of it and the vector 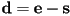
- if
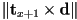 is positive, then
is positive, then 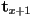 is below the line
is below the line - how many floating point operations (FLOPS) does this require per iteration?
- note that
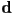 can be pre-computed before the loop
can be pre-computed before the loop - two additions to get
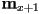
- two subtractions to get
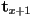
- two multiplications and one subtraction to get
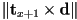 (recall that only the
(recall that only the 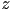 component will be non-zero for the cross product of two 2D vectors extended to 3D with
component will be non-zero for the cross product of two 2D vectors extended to 3D with  )
) - total: 7 FLOPS per iteration using cross product
- we can do better, and we want to, because we may have many lines to draw, and the midpoint algorithm is linear in the maximum difference in
 or
or  coordinates from
coordinates from 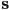 to
to 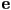
- idea 2: use the implicit form of the line
- can be shown (see text or L3) that
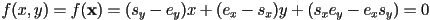 is an implicit form for the line through the points
is an implicit form for the line through the points 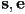
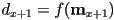 will be zero if
will be zero if 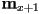 is on the line, positive if above, and negative if below (to prove that the signs work out like this, consider
is on the line, positive if above, and negative if below (to prove that the signs work out like this, consider  )
)- FLOP count:
- two additions to get
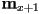
- two multiplies and two additions to evaluate
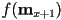
- total: 6 FLOPS per iteration using implict line eqn directly
- this is not much better than using the cross product, but it sets the stage for an incremental approach
- idea 3: observe that if we know the value of
 for a given point
for a given point 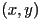 , we can use that value to accelerate the computation of nearby points:
, we can use that value to accelerate the computation of nearby points: - so now if we initialize
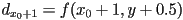 before the loop, we can make condition simply check if
before the loop, we can make condition simply check if 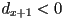
- if so, we need to move up, and next time through we will need
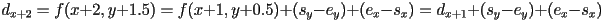
- if not, we will not move up, and next time through we will need
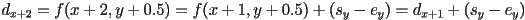
- revised pseudocode:
 (start at bottom)
(start at bottom)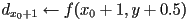
- for
 to
to 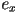 do (iterate from left to right)
do (iterate from left to right)- turn on pixel
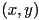 (we are now “on” a line pixel)
(we are now “on” a line pixel) - if
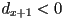 then
then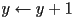 (need to move up)
(need to move up)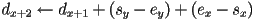
- else (don’t move up)
- FLOP count:
- one addition, assuming we pre-compute
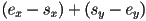 and
and 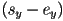
- total: 1 FLOP per iteration using incremental approach
Line Attributes
- line width
- dash patterns
- end caps: butt, round, square

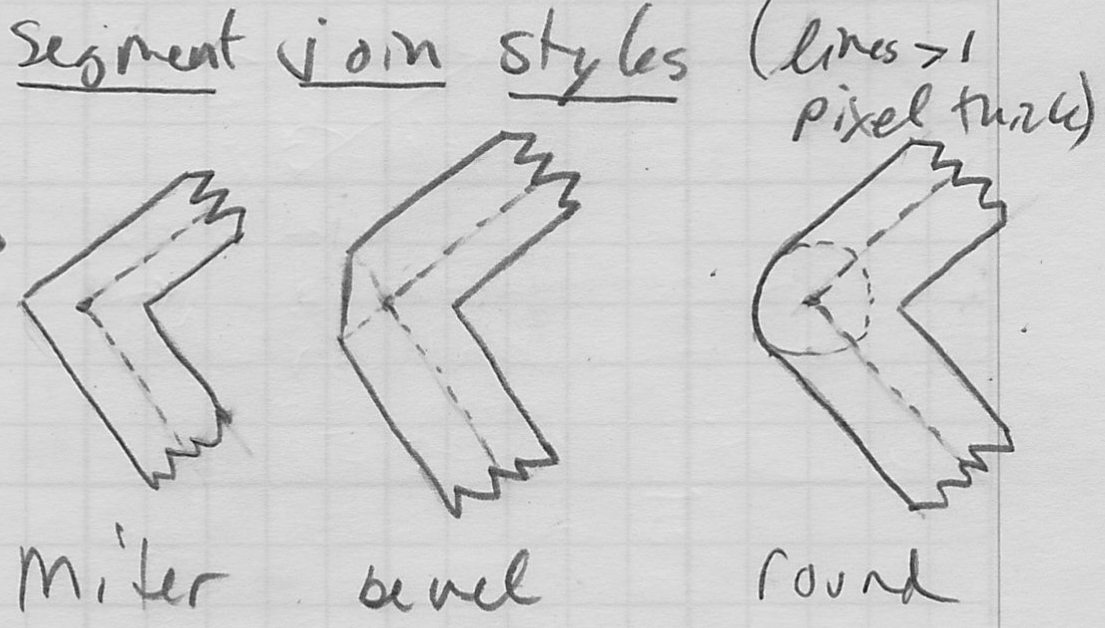
- joins: bevel, miter, round
Next Time
- sampling and antialiasing
- color perception and color spaces
- reading on website
 to
to 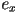 do (iterate from left to right)
do (iterate from left to right)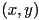 (we are now “on” a line pixel)
(we are now “on” a line pixel)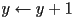 (need to move up)
(need to move up)
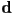 can be pre-computed before the loop
can be pre-computed before the loop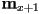
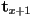
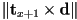 (recall that only the
(recall that only the 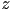 component will be non-zero for the cross product of two 2D vectors extended to 3D with
component will be non-zero for the cross product of two 2D vectors extended to 3D with  )
)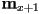
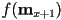
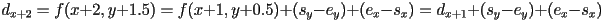
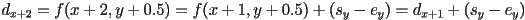
 to
to 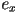 do (iterate from left to right)
do (iterate from left to right)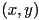 (we are now “on” a line pixel)
(we are now “on” a line pixel)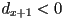 then
then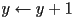 (need to move up)
(need to move up)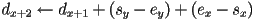
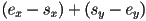 and
and