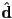Computer Graphics (CS 4300) 2010S: Lecture 3
Today
- HW1 due!
- review of segment and ray intersection
- “triangle asteroids” example
- lines in 2D
- output devices
“Triangle Asteroids”
- Asteroids is a classic 2D arcade game
- player is in space ship, tries to avoid being hit by flying asteroids
- can shoot the asteroids
- consider a version where each asteroid is a triangle
- how to determine if a “bullet” hits a triangle-asteroid?
- model bullet as a point
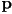
- at each frame, check if the point is inside any of the triangles
- how to check if point
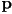 is inside a triangle?
is inside a triangle?- convert each triangle edge to
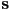 ,
, 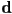 form, in CCW order
form, in CCW order 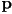 is inside if it is either on or to the left of each edge segment
is inside if it is either on or to the left of each edge segment- i.e. if
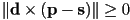 for each of the three segments
for each of the three segments - works because triangle is convex (intersection of half spaces)
- same alg works for any convex polygon
- what about non-convex? tessellate with triangles (will study later in course)
- how to determine if a “laser” hits the asteroid?
- model laser as a ray
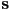 ,
, 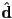
- at each frame, check if ray intersects any of the triangle edges
- this actually works for any polygon, not just triangles
- “corner cases” (both work fine given our intersection algorithm)
- ray touches asteroid only on a vertex
- ray coincident with an edge of the asteroid
Lines in 2D
- common “highschool” definition of a 2D line is given by the “slope-intercept” equation
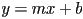
- line is the set of all points
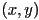 satisfying the equation
satisfying the equation 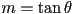 is slope, where
is slope, where 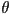 is angle from
is angle from  axis to line
axis to line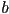 is y-intercept
is y-intercept- what about vertical lines?
- more general definition:
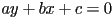
- but this is not unique: for
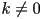
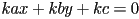 is same line
is same line
- both of these definitions are implicit: they specify a necessary and sufficient condition for points to lie on the line, but do not directly give a procedure for computing such points
- how many “degrees of freedom” does a line have in 2D? I.e., how many real numbers are both necessary and sufficient to define any line? (ans: 2)
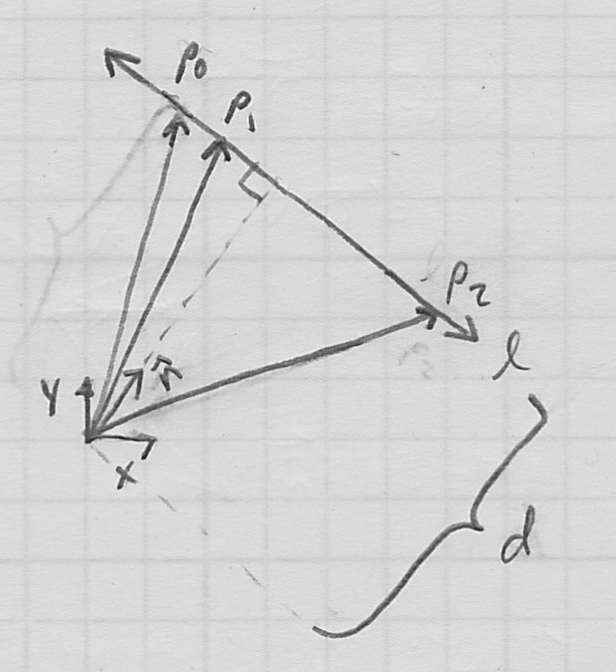
- one nice way to represent lines in 2D is by giving a unit normal vector
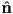 and a distance
and a distance 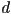 from the line to the origin
from the line to the origin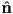 has 1DoF (its orientation; recall that its length constrained to 1),
has 1DoF (its orientation; recall that its length constrained to 1), 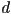 is the other
is the other- the line is then the locus of points
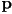 such that
such that 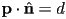 (read: the component of
(read: the component of 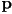 in the direction of
in the direction of 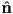 is
is 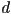 )
)
- note this is equivalent to the above algebraic form
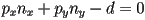 , i.e.
, i.e. 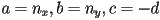
- but with an added constraint
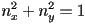
- if you are given a general set of coefficients
 you can divide whole equation by
you can divide whole equation by 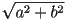 to enforce the constraint
to enforce the constraint
- signed distance from any given point
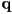 to the line is just
to the line is just 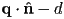
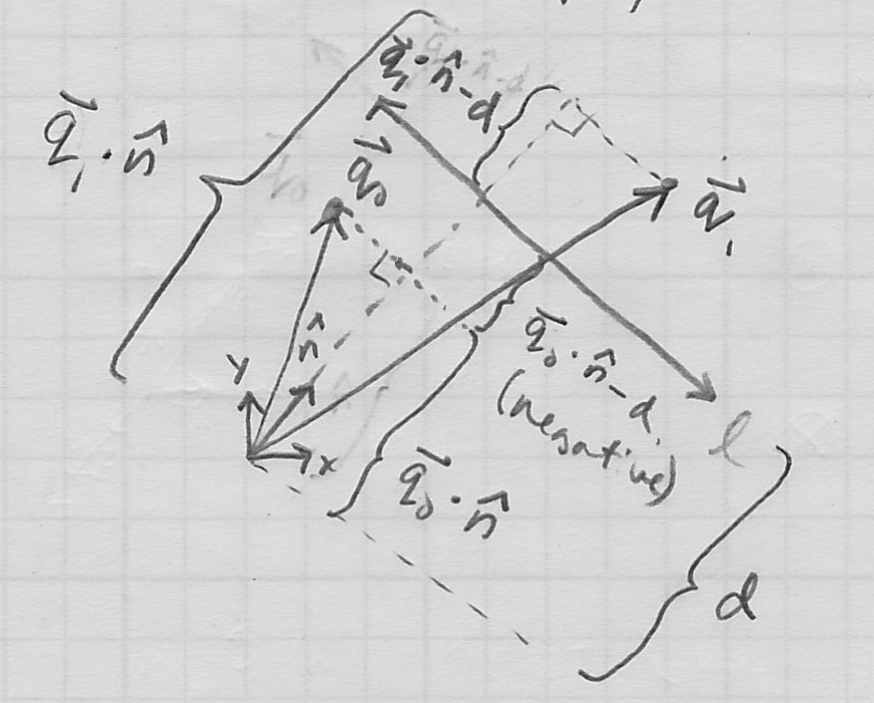
- positive if point is on the side of the line corresponding to the “outward facing” direction of
- zero if point is on the line (this observation is just a restatement of the line equation
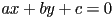 )
) - negative otherwise
- Note that this is just the value of the left hand side of the line equation, as long as the constraint
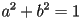 is satisfied. If that constraint is not satisfied, then the sign of the distance from
is satisfied. If that constraint is not satisfied, then the sign of the distance from 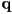 to the line is still correct, but the units (i.e. scale) of the distance will be off by
to the line is still correct, but the units (i.e. scale) of the distance will be off by 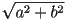 .
.
- how to get some point
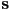 on the line?
on the line? 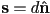
- how to get a unit vector
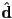 along the line?
along the line?  (remember, to take cross product of a 2D vector, extend to 3D with zero
(remember, to take cross product of a 2D vector, extend to 3D with zero 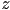 component)
component) - can use these to parametrize points
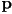 along the line as
along the line as 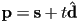
- exact same algorithm as above still works to compute intersection between lines, or between a line and a segment or ray. For the line(s) to intersect, there is no constraint on
 .
. - sometimes necessary to generate implicit equation of line through a segment given as
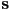 ,
, 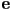 or as
or as 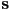 ,
, 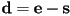
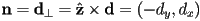 (not necessarily a unit vector, but still perpendicular to the line)
(not necessarily a unit vector, but still perpendicular to the line)- so
 and
and 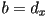 can be used as the first two constants in the implicit line equation
can be used as the first two constants in the implicit line equation - since
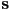 is a point on the line, can substitute in the implicit equation and solve for the remaining constant
is a point on the line, can substitute in the implicit equation and solve for the remaining constant 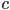
 , or
, or 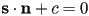 , so
, so 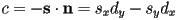
- expanding this out shows that
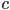 can be calculated directly from
can be calculated directly from 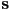 and
and 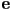 , if desired (the book does it this way, but its not necessarily any more efficient, especially if you started with a segment in
, if desired (the book does it this way, but its not necessarily any more efficient, especially if you started with a segment in 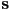 ,
, 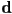 form)
form) 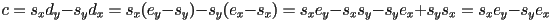
- this is a correct implicit equation for the line. If we want, we can now divide the whole equation by
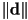 to make
to make  a unit vector. This extra computation is not required, but might make future computations more efficient. Depends on what we are intending to do with the equation.
a unit vector. This extra computation is not required, but might make future computations more efficient. Depends on what we are intending to do with the equation. - i.e.
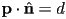
- with
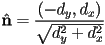
- and
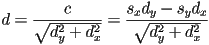
Output Devices
- a raster is a rectangular array of pixels (picture elements)
- common raster output devices include CRT and LCD monitors, ink jet and laser printers
- typically considered as top-to-bottom array of left-to-right rows, because that is how CRTs are (were) typically scanned
- for this reason, device (e.g. on-screen) coordinate frame typically has origin in upper left,
 axis aims to right, and
axis aims to right, and  axis aims down
axis aims down - (native) resolution of the device is the dimensions
 (note this is reverse of typical way we write matrix dimensions) of its raster output hardware
(note this is reverse of typical way we write matrix dimensions) of its raster output hardware- typical resolutions for monitors are 640x480 (VGA, the archaic but celebrated Video Graphics Array), 800x600, 1024x768, 1280x1024, 1600x1200, etc
- horizontal resolution often finer, again due to original CRT hardware: screens are typically rectangular with a 4:3 aspect ratio (they are wider than they are tall), so to have square pixels, the horizontal resolution must be greater
- higher resolution is generally “better” because finer detail can be represented
- more computation required for more pixels though, and more pixels makes the display hardware more expensive
- however monitors usually can display lower or higher (within some limits) resolution images than their native resolution by scaling (we will study how to scale images later in the course)
- how are rasters represented computationally?
- for a monochrome image, each pixel corresponds to one bit (also called a binary image)
- typically in graphics we use at least a greyscale images, where
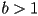 bits are used to represent the intensity at each pixel. The number of representable gray levels at each pixel is thus
bits are used to represent the intensity at each pixel. The number of representable gray levels at each pixel is thus 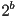 (
(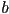 is typically a multiple of 8).
is typically a multiple of 8). - for a color image, compose multiple greyscale images, where each corresponds to a different color component. Three images corresponding to red, green, and blue color components are one typical arrangement. The images can be stored as independent planes or they may be interleaved, see below.
- we will study color in more detail later in the course
- in-memory representation of a raster
- monochrome image is typically a linear array of
 bytes, where
bytes, where 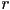 and
and 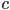 are the number of rows and columns in the raster, and
are the number of rows and columns in the raster, and  is the number of bytes per pixel
is the number of bytes per pixel - value of pixel at location
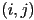 is thus stored in the
is thus stored in the  bytes at memory location
bytes at memory location 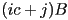 relative to the beginning of the array
relative to the beginning of the array - if
 , the order of bytes within the pixel value is typically determined by the byte order of the computer, which may be little-endian (least significant byte first) or big-endian (most significant byte first). Nowadays, little-endian is more common (e.g. Intel x86). Big-endian may still be encountered on e.g. PowerPC architectures (which is what Apple used in Mac computers up to around 2006).
, the order of bytes within the pixel value is typically determined by the byte order of the computer, which may be little-endian (least significant byte first) or big-endian (most significant byte first). Nowadays, little-endian is more common (e.g. Intel x86). Big-endian may still be encountered on e.g. PowerPC architectures (which is what Apple used in Mac computers up to around 2006). - sometimes
 is padded with one or more empty bytes so that pixels are aligned on word boundaries, which can actually make memory access more efficient in practice (at the expense of wasting some memory)
is padded with one or more empty bytes so that pixels are aligned on word boundaries, which can actually make memory access more efficient in practice (at the expense of wasting some memory) - for color images, either store as (typically three) separate monochrome rasters (planes), or interleave by packing all color components for a pixel into a contiguous block of memory (interleaved is more common now)
- the order of the color components, as well as the number of bits per component, is called the pixel format
- common pixel formats today include 24-bit RGB (
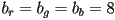 ) (“over 16 million colors!”), 32-bit RGB (typically same as 24 bit but with one byte of padding), 16-bit 5:6:5 RGB (
) (“over 16 million colors!”), 32-bit RGB (typically same as 24 bit but with one byte of padding), 16-bit 5:6:5 RGB (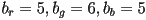 ) (human eye is most sensitive to green; this format is common for lower-quality video because it generally looks ok for images of real-world scenes and it uses only 2 bytes per pixel, reducing filesize)
) (human eye is most sensitive to green; this format is common for lower-quality video because it generally looks ok for images of real-world scenes and it uses only 2 bytes per pixel, reducing filesize)  still works with
still works with 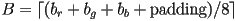
- byte ordering (little- vs big-endian) usually only matters within each color component, i.e. only if
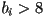 for some color component
for some color component 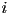
- In-memory raster is called a frame buffer when hardware is set up so that changes to memory contents drive pixel colors on the display itself. Most modern display hardware has a such a frame buffer.
- in fact, generally more than one, and can switch among them
- a common way to produce a smooth-looking animation is to use two buffers: the front buffer is rendered to the screen, and the back buffer is not
- this is called double buffering
- Each new frame of the animation is drawn onto the back buffer. Because it can take some time (hopefully not too long) to draw, this avoids seeing a “partial frame”.
- once the drawing is complete, the buffers are swapped
- how to render images of geometry, say line segments or triangles, onto a raster display?
- need to figure out what pixels to “light up” to draw the shape
- this is the process of rasterization
- will study line segment rasterization in the next lecture, triangles later in the course
- raster output is not the only way, another approach is “vector output”
- this is yet another related use of the word “vector”
- historically, vector displays were developed first
- CRT is made to scan line segments by steering electron beam from start to end of each segment (can generalize to curves)
- potentially more efficient because only need to scan along the actual line segments vs always scanning a raster across the whole screen
- but how to draw images of real-world scenes, and how to deal with color?
- nowadays, vector output is sometimes still encountered on a pen plotter, but even these are mostly antiques
- vector representation concept is still important, because computationally (i.e. not in hardware, but in software), some systems represent graphics in a vector form. These include PostScript, PDF (portable document format), and SVG (scalable vector graphics), though all can also include rasters.
- essentially, in a vector format, a picture is stored not as an array of pixels, but as a list of instructions about how to draw it
- vector format is “better” for some kinds of images, particularly line drawings and images (e.g. cartoons or computer art) other than “real-world” scenes
- since the actual geometry, vs a sampling of it, is stored, vector images can generally be scaled to larger or smaller sizes without any loss of quality
- the text uses the term “resolution independent” to describe the same thing
- vector images may also require less memory to store, and may be more compressible
Next Time
- HW2 out
- rasterizing line segments
- line attributes
- reading on website
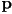
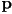 is inside a triangle?
is inside a triangle?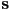 ,
, 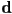 form, in CCW order
form, in CCW order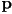 is inside if it is either on or to the left of each edge segment
is inside if it is either on or to the left of each edge segment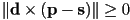 for each of the three segments
for each of the three segments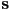 ,
,