19 Homework 12A
Due:
Tuesday, 4/2 at 9PM
This assignment may be done with an approved PARTNER.
This assignment is entirely AUTOGRADED.
What to Download:
Please start with this file, filling in where appropriate, and submit your homework to the HW12A assignment on Gradescope. This page has additional information, and allows us to format things nicely.
19.1 Consistent global state
Per Wikipedia, the Chandy–Lamport algorithm is a snapshot algorithm that is used in distributed systems for recording a consistent global state of an asynchronous system. It was developed by and named after Leslie Lamport and K. Mani Chandy.
19.2 Problem 1
Before we implement snapshotting, first we will implement a snapshot-less concurrent system. In this system, our processes will represent banks, and each bank will start with STARTBAL money, and will randomly transfer any amount of it to another random bank at the beginning. Every time they receive a transfer they will each keep sending transfers as long as they have not received MAX-TRANSFERS. If they have, they will keep accepting the incoming transfers but will no longer send any out.
The following is a diagram that shows a simplified version for three banks, where STARTBAL is 10 and MAX-TRANSFERS is 2:
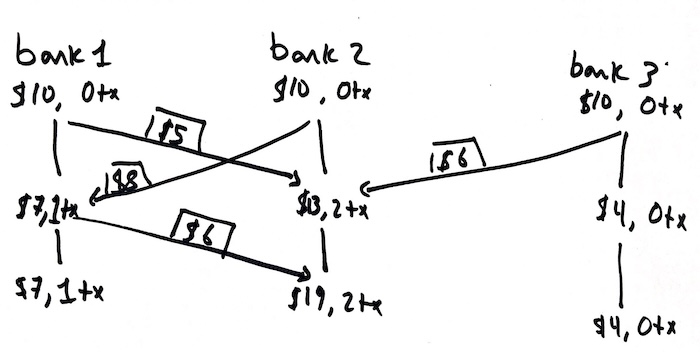
Note, in particular, that since new transfers are only sent when an existing transfer is received, it is likely that not all banks will get to MAX-TRANSFERS, and some may go above it (since we never reject incoming transfers) – as you can see in the above example. The point of the MAX-TRANSFERS is only to make the entire program stop; in a realistic system, this would run forever, but in our simplified setting we can only inspect once things are finished, so we need a termination condition.
The other thing about the diagram, which may seem confusing at first, is that each state is shown as it would be after receiving the incoming transfer (adding to the balance above) and after sending the outgoing one, if there is an outgoing one (subtracting from the resulting balance).
So, e.g., looking at "bank1", it starts with $10. After sending $5, it has $5, so after receiving $8 and sending $6, it is up $2, for a new balance of $7.
To implement this, you should use the following data definitions for the bank state and for the messages that they send, and use the constant as the starting balance for all banks:
| (define STARTBAL 1000) |
| (define MAX-TRANSFERS 20) |
| (define-struct bank-state-v1 (balance num-transfers other-banks)) |
| (define-contract BS1 (BankStateV1 Natural Natural (List String))) |
| (define-struct transfer (bal)) |
| (define-contract Transfer~ (Transfer Natural)) |
Define a bank-start-v1 handler that sends an initial transfer to another bank in the system. Note that the num-transfers is recording transfers received, so none should be recorded yet.
| (: bank-start-v1 (-> (List String) (Action BS1))) |
| (define (bank-start-v1 others) ...) |
Next implement bank-receive-v1 that handles receiving Transfer~ messages. On receipt, you should add to the balance of the current bank, increment the number of transfers received, and assuming you haven’t reached MAX-TRANSFERS, create another random transfer of any amount of the current balance.
| (: bank-receive-v1 (-> BS1 (ReceivePacket Transfer~) (Action BS1))) |
| (define (bank-receive-v1 st pkt) ...) |
Now, define a bank-process-v1 function that takes a name and produces a bank process with that name.
| (define (bank-process-v1 nm) ...) |
And finally, define a zero argument function bank-v1 that runs the simulation with 5 bank processes.
| (define (bank-v1) ...) |
19.3 Chandy-Lamport
An obvious correctness property that a bank (or network of banks) would want to maintain is that money doesn’t disappear (or appear). But this turns out to be a little tricky.
If you look at the intermediate timestep in the example above, you might notice something odd: since the bank state is recorded after receiving an incoming transfer and sending an outgoing one (assuming one is to be sent), even if it were possible to capture "all the states at a given time" (generally impossible, given the difficulty of synchronizing clocks), doing so would make it look like money had disappeared: our second row has $7, $13, and $4, which add to $24, not $30. The reason, of course, is that transfers "in flight" are also part of the total money in the system. In this very simple example, the $6 transfer out of "bank1" explains the difference, since both "bank2" and "bank3" have no outgoing transfers.
To solve this problem, Chandy and Lamport came up with an algorithm to record a consistent "snapshot" of the system. In our case, what this means is at a certain moment in time, we will initiate a snapshot recording balances, and any transfers that are in progress will be added to the snapshot balances of their recipients, but any new transfers will not be included. As a result, the snapshot balances should sum to the total amount of money in the system, which ideally, is the same amount of money as started in the system!
In order to explain how this works, we need to extend the above example; here we have the transfers go until there are three transactions, but additionally, there are special "marker" messages (marked as "M" in the diagram):
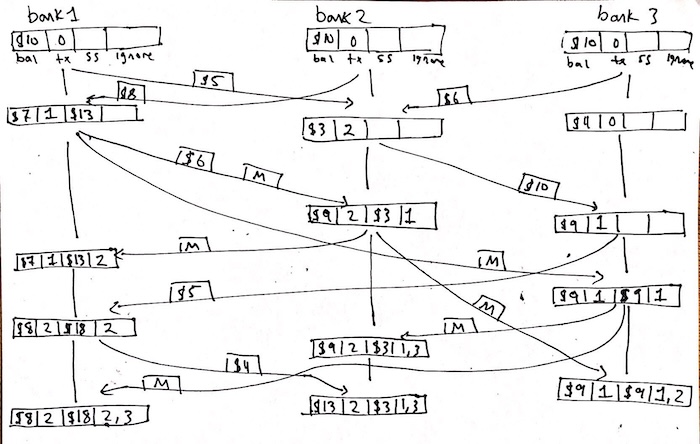
The idea of the algorithm is that, at any point, one party can initiate a snapshot (if multiple do at the same time, that’s fine too). In this case, "bank1" decides to snapshot after receiving the first $8 transfer from "bank2", but before sending $6 back to "bank2".
In order to support this, we need to extend our data definition to include a field for a snapshot (the third field, written "ss" at the top of the page), and a field of parties to ignore: we’ll get to that in a moment.
When "bank1" decides to start the snapshot, it copies the current balance into the snapshot, and then sends out the marker messages to all other banks telling them to initiate a snapshot. Now, if it could guarantee there were no transfers in transit, obviously they could all just record their own snapshot balance and there would be no algorithm. But the problem, of course, is that there may already be transfers in progress. So when a bank receives the marker message, it does record its current balance (so, "bank2" stores $3, as that’s what it is at the moment the marker comes).
But, in order to support transfers that were already in flight, when a bank receives a marker it does two things: first, it marks that it should ignore transfers from the sender, where ignoring means that future transfers should not be incorporated into the snapshot. The idea is that since the sender just sent it a marker, any transfers that the sender makes later occur after the snapshot, so shouldn’t be part of the snapshot.
The second thing it does is re-broadcast the marker to all other banks, including the one that sent it.
We can see how this ignoring comes into play when we see how "bank1" and "bank3" interact. "bank1" initiated the snapshot and sent a marker to "bank2" and "bank3". When "bank3" received it, it had already sent a $5 transfer back to "bank1". So while it recorded its current balance ($9) as its snapshot, that $5 in flight needs to be accounted for, as it was sent before the snapshot was initiated.
When "bank3" makes its snapshot, it then sends marker messages to all, including to "bank1". So there are now two messages in flight from "bank3" to "bank1": first, the $5 transfer, and second, the marker message. This is where the ignoring comes into play. Since "bank1" has not received a marker message from "bank3", everything it receives from "bank3" is from before the snapshot, which means the $5 transaction should be added not only to the regular balance, but to the snapshot balance as well.
This is in contrast to the $4 transfer from "bank1" to "bank2" near the bottom, which happens after "bank2" has received the marker from "bank1", and thus temporally after the snapshot. Thus, it is added to the regular balance but not the snapshot balance.
You can see, at the end of this sequence of operations, the sum of the snapshot balances, while not reflecting the same final balances (which makes sense, since more transfers happened after the snapshot; and in general, this kind of system would never stop, so there would be no final balances!), do add up to $30!
19.4 Problem 2
Your task is to implement the above algorithm. Use the following amended data definitions:
| (define UNTIL-SNAPSHOT 10) |
| (define-struct bank-state (balance num-transfers other-banks snapshot ignored)) |
| (define-contract BS (BankState Natural Natural (List String) (Maybe Natural) (List String))) |
| (define-struct marker ()) |
| (define-contract Message (OneOf Transfer~ (Marker))) |
Specifically, you should define bank processes that operate as in Problem 1, but once they have seen UNTIL-SNAPSHOT transfers, unless they are already snapshotting, they should, with probability 1/2, initiate a snapshot.
This means, as above, they record their balance before sending out the next transfer, and send out marker messages to all other banks before sending out the next transfer.
Receiving a marker message should, if no marker has been seen, cause a snapshot to be taken, markers to be broadcast, and the sender to be added to the ignored list. If a snapshot has already been taken, then the sender should be added to the ignored list, but no other action should be taken.
Receiving normal transfers must be amended as well, to take into account if a snapshot is ongoing: this must involve the ignored list, as described above.
You should implement the following functions to carry this out:
| (: bank-start (-> (List String) (Action BS))) |
| (define (bank-start others) ...) |
| (: bank-receive (-> BS (ReceivePacket Message) (Action BS))) |
| (define (bank-receive st pkt) ...) |
| (define (bank-process nm) ...) |
| (define (bank) ...) |
Write lots of unit tests on your bank-receive handler. The diagram above could probably be turned into a dozen, and that’s also probably not enough.
Your bank-receive handler should be structured into one big cond: with each of the possible cases combining the type of message, the state of the snapshot field, and membership in the ignored field.
You may wish to also define helpers for common tasks, i.e., defining a random outgoing transfer in case that num-transfers is under MAX-TRANSFERS.
19.5 Problem 3
Write a single argument predicate, snapshot-correct? that takes as argument the output of running bank and returns #t if the total as recorded in all the snapshot fields sums up to the number of banks multiplied by the STARTBAL constant. Don’t hardcode either, so that you can easily change the number of processes or starting balance.