►Fundamentals II
Introduction to Class-based Program Design
▼Assignments
►Assignment 10: Maze of twisty passages
On this page:
10.1 ???
10.1.1 Requirements
10.1.2 Kruskal’s Algorithm for constructing Minimum Spanning Trees
10.1.3 The Union/  Find data structure
10.1.3.1 Example
10.1.4 Putting the union/  find data structure to work
10.1.5 Breadth- and depth-first search
7.7
    ← prev  up  next → 

Assignment 10: Maze of twisty passages

This assignment is due in two parts.

Part 1: Due April 20, at 9pm, the GUI

Part 2: Due April 27, at 9pm, the animation of BFS and DFS solving the maze.

10.1 

Goals: Practice working with graphs and graph algorithms by designing mazes using Kruskal’s algorithm, and solving them using either breadth- or depth-first searches.

You will be using the Impworld library — make sure that at the top of your file, you include
import java.util.ArrayList;
import tester.*;
import javalib.impworld.*;
import java.awt.Color;
import javalib.worldimages.*;

In class, we have been discussing various algorithms for working with graphs, that require the use of several data structures working together. We have talked about general-purpose maze searching algorithms, like breadth- and depth-first searches, and we have talked about building minimum spanning trees on graphs.

To get a visual grasp of how these algorithms work, you are going to be building and solving mazes, like this one:

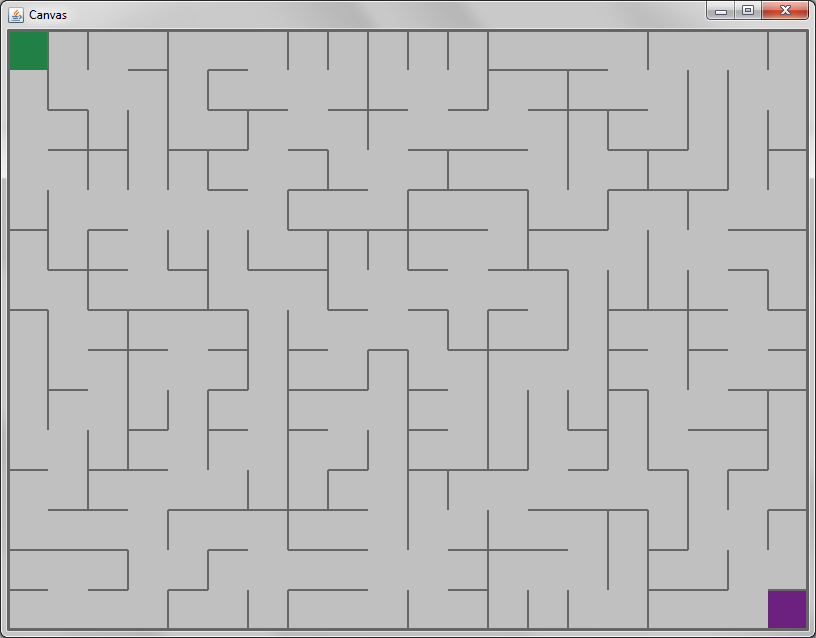
The mazes you construct should start in the upper-left corner (shown in green) and end in the lower-right corner (shown in purple). As you solve the mazes, you should color in the cells you have explored. Once you have reached the solution, you must backtrack the path from the end to the start, and draw it as well. A fully-solved maze might look like this:

Your code must handle mazes of arbitrary sizes, up to at least 100x60:

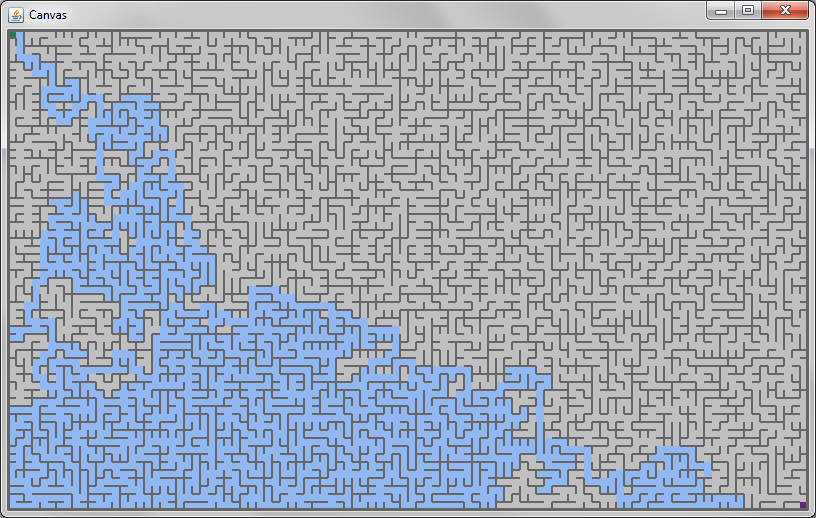
In particular, your code must not crash with stack overflows...

10.1.1 Requirements

Your program should support at minimum the following features:

Part 1:

  • Construct and display random mazes graphically using Kruskal’s algorithm and Union/Find (below). When running the program the output should look similar to the first picture above.

Part 2:

  • Display the maze graphically and animate the search for the path.

  • Allow the user to choose one of two algorithms for finding the path: Breadth-First Search or Depth-First Search (below). If the user presses the ’B’ key, the maze will be solved via BFS, if the user presses the ’D’ key, the maze will be solved via DFS.

  • Display the solution path connecting the start and end, once it’s found

As always, be sure to test your code thoroughly.

Additionally, you may attempt the following features for extra credit.

Eextra credit will only count if they are convincingly and thoroughly tested, and if the rest of the assignment is completed equally thoroughly — you will not receive extra credit if the minimum functionality does not work properly.

Extra credit features:

  • Allow the user the ability to start a new maze without restarting the program.

  • Keep the score of wrong moves and keep statistics on which one of the two algorithms had fewer steps for each maze.

  • In addition to animating the solution of the maze, also animate the construction of the maze: on each tick, show a single wall being knocked down.

  • Color every square with a gradient of colors indicating how far it is from the start of the maze. E.g. red means very close to the start, and blue means very far.

Spend careful thought planning ahead and designing your classes: if your design is too brittle, you’ll have a very hard time completing the algorithms. And as always, have fun!

10.1.2 Kruskal’s Algorithm for constructing Minimum Spanning Trees

Here is Kruskal’s algorithm illustrated on a particular example graph: 
A -----30------- B -----50------- F
 \             / |               /
  \           /  |              /
  50        35  40            50
    \       /    |            /
     \     /     |           /
      \   /      |          /
        E --15-- C ---25-- D
(The edges are drawn without directional arrows; in your mazes, every maze cell will be connected to its four neighbors, so edges are effectively undirected. Edge weights are notated as numbers on the edges.)

Kruskal’s algorithm begins by sorting the list of edges in the graph by edge weight, from shortest to longest: 
(E C 15)
(C D 25)
(A B 30)
(B E 35)
(B C 40)
(F D 50)
(A E 50)
(B F 50)

At each step we remove the shortest edge from the list and add it to the spanning tree, provided we do not introduce a cycle. In practice, this may produce many trees during the execution of the algorithm (so in fact, the algorithm produces a spanning forest while it runs), but they will eventually merge into a single spanning tree at the completion of the algorithm.

For this particular graph, we add the edges (E C 15), (C D 25), (A B 30) and (B E 35). When we try to add the edge (B C 40) we see that it would make a cycle, so this edge is not needed and we discard it. We then add edge (F D 50). This connects the last remaining unconnected node in the graph, and our spanning tree is complete. In very high-level pseudocode, the algorithm is quite short and elegant:

while (we do not yet have a complete spanning tree)

  find the shortest edge that does not create a cycle

  and add it to the spanning tree

Determining if we have a complete spanning tree is easy: for \(n\) nodes, we need \(n-1\) edges to connect them all.

Do Now!

Why can’t we have fewer edges? Why can’t we have more?

We can represent the spanning tree itself by a list of edges. Adding an edge to that list is as easy as Cons’ing it on, or adding it, depending on which representation of lists you choose to use. Finding the shortest edge is easy, since we began by sorting the list of edges by their weights. The only tricky part in this algorithm is figuring out whether a given edge creates a cycle with the edges we have already selected. For this we use the Union/Find data structure.

10.1.3 The Union/Find data structure

The goal of the union/find data structure is to allow us to take a set of items (such as nodes in a graph) and partition them into groups (such as nodes connected by spanning trees) in such a way that we can easily find whether two nodes are in the same group, and union two disjoint groups together. Intuitively, we accomplish this by naming each group by some representative element, and then two items can be checked for whether they are in the same group by checking if they have the same representative element.

10.1.3.1 Example

In class, we represented every node of the graph as a class with a String name field. (For this assignment, String names will be inconvenient; you will need to come up with some other uniquely-identifying feature of each cell in a maze that can serve the same role as a name.) Then the union-find data structure was a HashMap<String, String> that mapped (the name of) each node to (the name of) a node that it is connected to. Initially, every node name is mapped to itself, signifying that every node is its own representative element, or equivalently, that it is not connected to anything.

Recall the example from above: 
A -----30------- B -----50------- F
 \             / |               /
  \           /  |              /
  50        35  40            50
    \       /    |            /
     \     /     |           /
      \   /      |          /
        E --15-- C ---25-- D

Our HashMap will map every node name to itself: 
                                     Representatives, visually:
        +---+---+---+---+---+---+    A     B     C     D     E     F
Node:   | A | B | C | D | E | F |
        +---+---+---+---+---+---+
Link:   | A | B | C | D | E | F |
        +---+---+---+---+---+---+


Spanning tree so far:
Kruskal’s algorithm begins by sorting the list of edges in the graph by edge weight, from shortest to longest: 
(E C 15)
(C D 25)
(A B 30)
(B E 35)
(B C 40)
(F D 50)
(A E 50)
(B F 50)

When we add edge (E C 15), nodes E and C are now connected: 
                                      Representatives, visually:
        +---+---+---+---+---+---+     A     B     D     E     F
Node:   | A | B | C | D | E | F |                       ^
        +---+---+---+---+---+---+                       |
Link:   | A | B | E | D | E | F |                       C
        +---+---+---+---+---+---+

Spanning tree so far:          (C E)
We next add edge (C D 25). Since C’s representative is E, and D’s representative is D, they are currently separate, so adding this edge would not create a cycle. We can therefore union them and set D’s representative’s representative to C’s representative: 
                                      Representatives, visually:
        +---+---+---+---+---+---+     A     B     E     F
Node:   | A | B | C | D | E | F |                 ^
        +---+---+---+---+---+---+                / \
Link:   | A | B | E | E | E | F |               C   D
        +---+---+---+---+---+---+

Spanning tree so far:          (C D) (C E)

Do Now!

Careful! Why must we union the representatives of two nodes, and not the nodes themselves?

Next we add edge (A B 30): 
                                      Representatives, visually:
        +---+---+---+---+---+---+     A     E     F
Node:   | A | B | C | D | E | F |     ^     ^
        +---+---+---+---+---+---+     |    / \
Link:   | A | A | E | E | E | F |     B   C   D
        +---+---+---+---+---+---+

Spanning tree so far:          (A B) (C D) (C E)

We now have three connected components: Nodes B and A form one of them, node F is a singleton, and nodes C, D, and E are in the third component.

We add edge (B E 35). That means we add a link from the representative for B (which is A) to the representative for node E (which is E): 
                                      Representatives, visually:
        +---+---+---+---+---+---+       E     F
Node:   | A | B | C | D | E | F |       ^
        +---+---+---+---+---+---+      /|\
Link:   | E | A | E | E | E | F |     A C D
        +---+---+---+---+---+---+     ^
                                      |
                                      B

Spanning tree so far:          (A B) (B E) (C D) (C E)

We still have two components. When we try to add the edge (B C 40) to the graph, we notice that the representative for node C is the same as the representative for the node B. Therefore adding this edge would create a cycle, so we discard it.

Finally, we add the edge (F D 50): after this, every node has the same representative, and therefore all nodes are connected: 
                                      Representatives, visually:
        +---+---+---+---+---+---+       E
Node:   | A | B | C | D | E | F |       ^
        +---+---+---+---+---+---+      /|\
Link:   | E | A | E | E | E | D |     A C D
        +---+---+---+---+---+---+     ^   ^
                                      |   |
                                      B   F

Spanning tree so far:          (A B) (B E) (C D) (C E) (D F)

10.1.4 Putting the union/find data structure to work

The full Kruskal’s algorithm needs a union/find data structure to handle efficiently connecting components, and also needs a list of the edges used by the algorithm:
HashMap<String, String> representatives;
List<Edge> edgesInTree;
List<Edge> worklist = all edges in graph, sorted by edge weights;
 
initialize every node's representative to itself
While(there's more than one tree)
Pick the next cheapest edge of the graph: suppose it connects X and Y.
If find(representatives, X) equals find(representatives, Y):
discard this edge // they're already connected Else:
Record this edge in edgesInTree
union(representatives,
find(representatives, X),
find(representatives, Y))
Return the edgesInTree
To find a representative: if a node name maps to itself, then it is the representative; otherwise, “follow the links” in the representatives map, and recursively look up the representative for the current node’s parent.

There are additional heuristics for speeding this algorithm up in practice, and they make for a very efficient algorithm. Unfortunately, analyzing these heuristics is beyond the scope of this course, but you can look up the “path-compression” heuristic if you are curious.

To union two representatives, simply set the value of one representative’s representative to the other.

Do Now!

Again, why must we only ever union two representatives, and not two arbitrary nodes?

10.1.5 Breadth- and depth-first search

As we worked through in class, breadth- and depth-first searches are very closely related algorithms. The essential steps of the algorithm are the same; the only difference is whether to use a queue or a stack.

HashMap<String, Edge> cameFromEdge;

???<Node> worklist; // A Queue or a Stack, depending on the algorithm

 

initialize the worklist to contain the starting node

While(the worklist is not empty)

  Node next = the next item from the worklist

  If (next has already been processed)

    discard it

  Else If (next is the target):

    return reconstruct(cameFromEdge, next);

  Else:

    For each neighbor n of next:

      Add n to the worklist

      Record the edge (next->n) in the cameFromEdge map

The cameFromEdge map is used to record which edge of the graph was used to get from an already-visited node to a not-yet-visited one. This map is used to reconstruct the path from the source to the given target node, simply by following the edges backward, from the target node to the node that it came from, and so on back to the source node. Unlike Kruskal’s algorithm, the worklist here is a collection of nodes (rather than edges). Like the union/find algorithm, there is a recursive traversal from one node to a previous one, using node names as the keys into the auxiliary map that accumulates the ongoing state of the algorithm.

    ← prev  up  next →