CS6200: Information Retrieval

Homework 2

Assigned: Friday, 2 October 2015
Due: Friday, 16 October 2015, 11:59 p.m.

PageRank

In this assignment, you will compute PageRank on a collection of 183,811 web documents. Consider the version of PageRank described in class. PageRank can be computed iteratively as show in the following pseudocode:

// P is the set of all pages; |P| = N
// S is the set of sink nodes, i.e., pages that have no out links
// M(p) is the set (without duplicates) of pages that link to page p
// L(q) is the number of out-links (without duplicates) from page q
// d is the PageRank damping/teleportation factor; use d = 0.85 as a fairly typical value

foreach page p in P
  PR(p) = 1/N                          /* initial value */

while PageRank has not converged do
  sinkPR = 0
  foreach page p in S                  /* calculate total sink PR */
    sinkPR += PR(p)
  foreach page p in P
    newPR(p) = (1-d)/N                 /* teleportation */
    newPR(p) += d*sinkPR/N             /* spread remaining sink PR evenly */
    foreach page q in M(p)             /* pages pointing to p */
      newPR(p) += d*PR(q)/L(q)         /* add share of PageRank from in-links */
  foreach page p
    PR(p) = newPR(p)

return PR

In order to facilitate the computation of PageRank using the above pseudocode, one would ideally have access to an in-link respresentation of the web graph, i.e., for each page p, a list of the pages q that link to p.

Consider the following directed graph:

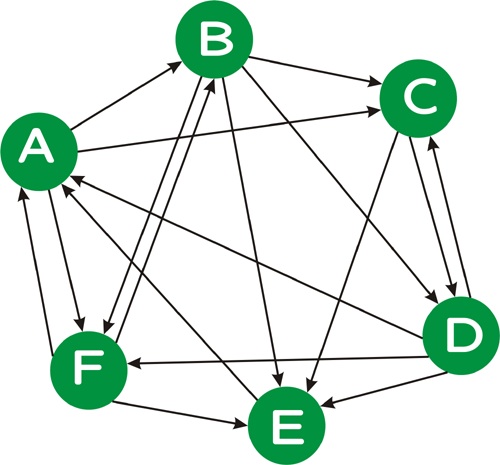
We can represent this graph as follows:

A D E F
B A F
C A B D
D B C
E B C D F
F A B D

where the first line indicates that page A is linked from pages D, E, and F, and so on. Note that, unlike this example, in a real web graph, not every page will have in-links, nor will every page have out-links.

Instructions

[10 points] Implement the iterative PageRank algorithm as described above. Test your code on the six-node example using the input representation given above. Be sure that your code handles pages that have no in-links or out-links properly. (You may wish to test on a few such examples.) In later parts of this assignment, your task will be easier if you don't require loading the entire link graph into memory.
Please hand in: a list of the PageRank values you obtain for each of the six vertices after 1, 10, and 100 iterations of the PageRank algorithm.
[20 points] Download the in-links file for the WT2g collection, a 2GB crawl of a subset of the web. This in-links file is in the format described above, with the destination followed by a list of source documents.
Run your iterative version of PageRank algorithm until your PageRank values "converge". To test for convergence, calculate the perplexity of the PageRank distribution, where perplexity is simply 2 raised to the (Shannon) entropy of the PageRank distribution, i.e., 2^H(PR). Perplexity is a measure of how "skewed" a distribution is: the more "skewed" (i.e., less uniform) a distribution is, the lower its preplexity. Informally, you can think of perplexity as measuring the number of elements that have a "reasonably large" probability weight; technically, the perplexity of a distribution with entropy h is the number of elements n such that a uniform distribution over n elements would also have entropy h. (Hence, both distributions would be equally "unpredictable".)

Run your iterative PageRank algorthm, outputting the perplexity of your PageRank distibution until the change in perplexity is less than 1 for at least four consecutive iterations.

One hint is that in this dataset, the document with the highest in-link count and the highest PageRank is the same, so don't worry that it's a bug.

Please hand in: a list of the perplexity values you obtain in each round until convergence as described above.
[40 points] Sort the collection of web pages by the PageRank values you obtain.
Please hand in:
- a list of the document IDs of the top 50 pages as sorted by PageRank, together with their PageRank values;
- a list of the document IDs of the top 50 pages by in-link count, together with their in-link counts;
- the proportion of pages with no in-links (sources);
- the proportion of pages with no out-links (sinks); and
- the proportion of pages whose PageRank is less than their initial, uniform values.
[30 points] Examine the top 10 pages by PageRank and the top 10 by in-link count in the Lemur web interface to the collection by using the "e=docID" option with database "d=0", which is the index of the WT2g collection. For example, the link

http://fiji4.ccs.neu.edu/~zerg/lemurcgi_IRclass/lemur.cgi?d=0&e=WT04-B22-268
or
http://karachi.ccs.neu.edu/~zerg/lemurcgi_IRclass/lemur.cgi?d=0&e=WT04-B22-268
will bring up document WT04-B22-268, which is an article on the Comprehensive Test Ban Treaty.
Please hand in: Speculate why these documents have high PageRank values, i.e., why is it that these particular pages are linked to by (possibly) many other pages with (possibly) high PageRank values. Are all of these documents ones that users would likely want to see in response to an appropriate query? Give some examples of ones that are and ones that are not. For those that are not "interesting" documents, why might they have high PageRank values? How do the pages with high PageRank compare to the pages with many in-links? In short, give an analysis of the PageRank results you obtain.

Final requests

In addition to the written items mentioned above, you should hand in a copy of your source code, which should hopefully be relatively short, and instructions on (compiling and) running it. The only input to your code should be a file in the in-link format described above. The output should be a list of page IDs and their PageRank values.