Lecture 13: Tuples and Memory Allocation

8.3

Lecture 13: Tuples and Memory Allocation

1 Computing with arbitrary-sized data

So far, our compiler supports a language with arbitrarily complex arithmetic and logical expressions, function definitions, and function applications. However, our only values are two primitives: integers and booleans. To make our language more fully-featured, we need the ability to handle structured, arbitrarily sized data.

At a high level, we know that there are three kinds of composite data:

Enumerated data types, with a finite set of distinct values
Structured data types, comprised of a finite set of pieces (either named as in structures, or positional as in arrays), where each piece is itself a value
Potentially-recursive union data, with a finite set of distinct categories of values, where each category of value could itself be structured, and where the pieces of those structures could themselves be union data.

The first kind of composite data really only manifests itself in the type system, where we need to be able to say, “These values are part of this enumeration, while those values are not.” Since enumerated data is merely a finite set of constants, we can simulate them merely by using some distinct set of integers.

Since union data is essentially an enumeration of structured data, if we had the ability to create structured data types, then we could encode union data types by adding a field to each value identifying which variant of the union this value belongs to.

But structured data does not admit such a simple encoding. It requires the ability to group several values into one, and use that compound thing as a value: it should be created by some expressions, used by others, and passed to and returned from functions. In other words, structured data is a fundamentally new thing in our language.

We can consider various kinds of structured data such as records with named fields (as in C structs or Racket define-structs), or indexed data like arrays. But the simplest form of structured data is the humble pair, and its bigger cousins the tuples.

Standard reminder: Every time we enhance our source language, we need to consider several things:

Its impact on the concrete syntax of the language
Examples using the new enhancements, so we build intuition of them
Its impact on the abstract syntax and semantics of the language
Any new or changed transformations needed to process the new forms
Executable tests to confirm the enhancement works as intended

2 Adding pairs to our language

2.1 Syntax and examples

We’ll write pairs as

‹expr›: ... | ( ‹expr› , ‹expr› )

For example, (4, 5) is a pair consisting of two numbers. The flexibility of our grammar, though, allows us to nest pairs inside one another, as in (3, (true || false, false)) or (((1, 2), 3), 4 + 5), or any other combination we might attempt. However, in order to use our pairs, we need to be able to access their components. We’ll do so with two new primitive operators

‹expr›: ... | fst ‹expr› | snd ‹expr›

The intended semantics are that these two primitives project out the first or second components of the pairs: fst (3, 4) == 3 and snd (4, (true, 5)) == (true, 5).

We can add these expression forms to our AST easily enough, modelling the new accessors as unary primitives:

type 'a expr = ...
  | EPair of 'a expr * 'a expr * 'a
type prim1 = ... | Fst | Snd

2.2 Representing pairs

Introducing pairs into our language is a much more invasive change than it might appear. For the first time, we have values in our language that are too big to fit into a register—after all, each component of a pair filled a register on its own! So where can we put them? One natural thought might be simply to put the two halves of the pair adjacent to each other in two consecutive stack slots, and perhaps some careful bookkeeping might remember that those two slots “go together”. But this fails for several reasons:

If we want to be able to use pairs as arguments to functions, we’d have to communicate to the callee that some of its arguments aren’t uniformly sized, so its initial environment can’t simply map the ith argument to RBP + 8 * (i + 2). Perhaps we could convey this information via static types, but it certainly would complicate passing pairs to runtime functions like print! This starts to break the calling convention, which breaks interoperability and therefore is not something to be done lightly.
If we want to be able to return pairs from functions, we have to figure out how to so without using RAX as the entirety of our answer. Again this breaks the calling convention, and so we should reconsider.
If we want to nest pairs inside each other, as in our examples above, then we immediately fail: In ((1, 2), 3), there simply is no way to put both 1 and 2 at consecutive stack slots (because they’re part of a pair), and also put that entire pair and 3 at consecutive stack slots — we need at least three slots!

Instead, we’re going to have to look elsewhere to store our pairs: we’re going to use the heap.

2.2.1 Introducing pointers

The heap is another region of memory, at numerically-smaller addresses than our stack, where we can potentially allocate space for whatever values we want. We’ll defer for a moment how exactly to do that, but suppose that we can. Then for each pair we have to evaluate, we can request space for two consecutive words of memory, and store the two halves of the pair in those two words. Crucially for us, the address of (the first of) those two words is unique: no other pair will exist at that exact address. And, even better, one address is small enough to fit into a register. We can use this address as the representation of our pairs: it is small enough to pass into and out of functions, and small enough to be placed into the components of another pair. By adding this indirection, we’ve solved all three of the failings above.

2.2.2 Tagging pair values

Of course, now that we have a new kind of value, we need a tag to go with it, to distinguish pairs from booleans or integers. We have three tags remaining, so we can arbitrarily choose one of them, say 0x1, to mark our pointers as pairs. This seems risky, though — unlike integers and booleans, whose representations we could choose for our own convenience, memory addresses are interpreted by the computer, so we can’t capriciously change bits in them! However, we only need three bits, which means if we can ensure that our values always end with three known bits, then we can carefully replace our tag bits with those three known bits before asking the computer to reinterpret our value as a pointer. (Note carefully the emphasis in wording here: a given 64-bit quantity is a value in our language while it is tagged, and becomes interpretable as a pointer when we replace the tag bits with whatever those bits should have been.)

The easiest set of known bits to work with is 0b000. Can we ensure that every memory address we allocate always ends in three zero bits? Yes! “Ends with three zero bits” is the same thing as saying “multiple of 8” Conveniently, our pairs are two words wide, which means they’re exactly 16 bytes long. If we can ensure that every allocation we make is aligned to an 8-byte boundary, then all our addresses will end in 0x000, which means we are free to use those three bits for whatever tag we need.

2.2.3 Allocating space on the heap

Where can we actually obtain memory from? One possibility is “just use malloc”, but that just defers the problem. Besides, we have no guarantees that malloc will enforce our 8-byte-alignment constraint. Instead, we’ll use malloc once, to obtain a big buffer of space to use, and we’ll manipulate that buffer directly from our assembly. (See below for how malloc actually gets itself started.)

Here is one possible strategy for handling memory; there are many others. Let’s devote one register, R15, to always store a pointer to the next available heap location. Then “allocating a pair” amounts to storing two values into [R15] and [R15 + 8], and then incrementing R15 by 16. (We’ll ignore out-of-memory errors and garbage collection, for now.) Once again, if R15 started off as a multiple of 8, then after this process it remains a multiple of 8, so our alignment invariant still holds.

All that remains is to initialize R15 appropriately, which requires collaboration between main and our_code_starts_here. We need to allocate a buffer of memory from main, using calloc to allocate-and-clear the memory, and then pass that pointer in to our code. In other words, our_code_starts_here now really is a function that takes in arguments—in this case, the “start of the heap”.

int main() {
  uint64_t* HEAP = calloc(1024, sizeof(uint64_t)); // Allocate 8KB of memory for now
  uint64_t result = our_code_starts_here(HEAP);
  print(result);
  free(HEAP);
  return 0;
}

Do Now!
Why must the call to free(HEAP) happen after the call to print(result)?

On the callee side, in our_code_starts_here, we need to store this provided address into R15, but we first need to ensure that it is a multiple of 8.1Multiples of 8 are actually guaranteed for us, but it is worthwhile to ensure this for ourselves, especially if for some reason we need a more stringent alignment guarantee later on. In particular, we need to round the address up to the nearest multiple of 8 (because rounding down might give us an unallocated address). The easiest way to achive this is to add 7 to the address, then round down to the nearest multiple of 8. Recall from Lecture 6: Checking for errors and calling functions that the first six arguments to a function are passed in registers, and our_code_starts_here is being called from main. So we can find the value of HEAP in register RDI:

our_code_starts_here:
  ...                              ;; basic function prologue as usual
  move R15, RDI                    ;; Load R15 with the passed-in pointer
  add R15, 7                       ;; \ add 7 to get above the next multiple of 8
  mov temp_reg, 0xfffffffffffffff8 ;; | load a scratch register with the necessary mask
  and R15, temp_reg                ;; / and then round back down.
  ...

Do Now!
Why couldn’t we do this rounding within main itself?

The indirection through temp_reg is necessary once again because of the limitation on 64-bit literals in and instructions.

Do Now!
For this particular sequence of instructions, what register could we use for temp_reg, and why? (Hint: it needs to be a register whose value is never needed again, since we’d overwrite its value...)

Do Now!
What small changes would be needed to ensure R15 has a 16-byte aignment? Speculate on any advantages or disadvantages such a choice might give us.

2.3 ANF transformations

Given that evaluating a pair actually performs a memory allocation, we cannot treat pairs as immediate values: the value simply isn’t immediately ready. But obviously we do want to be able to bind them to variables, so they must be compound expressions. This leads to a simple design:

type 'a cexpr =
  ...
  | CPair of 'a immexpr * 'a immexpr * 'a

We force the two components of the pair to be immediate, so that the only computational step happening here is the memory allocation itself.

Exercise
Complete helpC and helpI for EPair expressions.

2.4 Compiling pairs and pair accesses

We now have all the tools we need to generate code for all our pair-related expressions. To construct a pair,

... assume the two parts of the pair are already evaluated ...
mov [R15],     <first part of pair>
mov [R15 + 8], <second part of pair>
mov RAX, R15   ;; Start creating the pair value itself
add RAX, 0x1   ;; tag the pair
add R15, 16    ;; bump the heap pointer

The order of execution here is important: we must fully evaluate the two parts of the pair prior to creating the pair, or else the evaluation of each component might modify R15, leading to non-consecutive memory addresses for our pair. Fortunately, our ANF conversion ensured this for us. Next we must save the current value of R15 as our result RAX, so that we can tag it correctly.

To access the first element of a pair,

mov RAX, <the pair value>
<check that RAX is indeed a pair>
sub RAX, 0x1       ;; untag it
mov RAX, [RAX + 0] ;; treat RAX as a pointer, and get its first word

Accessing the second element uses mov RAX, [RAX + 8] instead.

2.5 Type Checking and Type Inference

Since pairs are a new type of value, it makes sense they need a new type constructor. Moreover since they are compound values, it makes sense that their types contain other types: the pair (3, 3) should not have the same type as (true, false). We will create a new type constructor

type 'a typ =
  ...
  | TyPair of 'a typ * 'a typ * 'a

that contains the types of the two components of the pair. Type-checking a pair is easy: we simply check the individual component expressions at the individual component types.

\begin{equation*}\dfrac{\Gamma \vdash e_1 : \mathsf{\tau_1} \quad \Gamma \vdash e_2 : \mathsf{\tau_2}}{\Gamma \vdash (e_1, e_2) : \mathsf{\tau_1 * \tau_2}}[\text{T-Pair}]\end{equation*}

Type-checking either fst or snd is more challenging, because we do not know a priori what type the other component of the pair should be.

Do Now!
Why not?

To make this tractable, we’ll restrict our typing rule to only permit type-checking fst e or snd e when e is a variable. The only way we could type-check a variable is by looking it up in the environment, which ensures that we have a complete type for it.

\begin{equation*}\dfrac{\Gamma(x) = \tau_1 * \tau_2}{\Gamma \vdash \operatorname{fst} x : \mathsf{\tau_1}}[\text{T-Fst}] \qquad\qquad \dfrac{\Gamma(x) = \tau_1 * \tau_2}{\Gamma \vdash \operatorname{snd} x : \mathsf{\tau_2}}[\text{T-Snd}]\end{equation*}

For type-inference, however, we need no such restriction: we just need to infer that e has some pair type at all:

\begin{equation*}\dfrac{\Gamma \vdash e : \mathsf{\tau_1 * \tau_2}}{\Gamma \vdash \operatorname{fst} e : \mathsf{\tau_1}} \qquad\qquad \dfrac{\Gamma \vdash e : \mathsf{\tau_1 * \tau_2}}{\Gamma \vdash \operatorname{snd} e : \mathsf{\tau_2}}\end{equation*}

3 Generalizing to tuples

Tuples are simply longer pairs. We could consider representing tuples as a linked-list of pairs, but that would be quite inefficient. Instead, we’ll generalize everything above that hard-coded “two elements” to become a list of elements. This has some consequences for our representation, and for type-checking and type-inference, but it mostly goes through smoothly.

3.1 Syntax and examples

We’ll write tuples as

‹expr›: ... | ( ) | ( ‹expr› , ) | ( ‹expr› , ‹expr› , ... ‹expr› )

A tuple can have zero or more fields, as in (3, 4), (), or (true, false, 5). The concrete syntax for a 1-field tuple is slightly odd, but is necessary to distinguish the tuple (1 + 2,) from the parenthesized expression (1 + 2). Accessing elements of a tuple can’t be restricted to two unary primitive operators now, because we don’t know in advance how large our tuples will be. Instead, we’ll add a more general expression

‹expr›: ... | ‹expr› [ NUM of NUM ]

Here, the expression e[0 of 5] evaluates to the first item of a 5-tuple, while e[4 of 5] evaluates to the last item of the tuple. The syntax here is slightly odd: we requires integer literals for the index, rather than expressions, and we require the programmer specify the size of the tuple. Both of these restrictions are needed to make type-checking and type-inference tractable, as we’ll see below.

We’ll represent tuples and tuple-accesses as

type 'a expr =
  ...
  | ETuple of 'a expr list * 'a (* components of the tuple *)
  | EGetItem of 'a expr * int * int * 'a (* tuple, desired index, size *)

Exercise
What are the various errors that could arise from these expressions?

Simply working through our pipeline:

It is an obvious well-formedness error to ask for a negative index, or an index equal to or greater than the provided upper bound.
It should be a type error to specify the wrong bound for a tuple, or to ask for an index outside those bounds.
Even if the type checker fails, it should be a dynamic error to access an out-of-bounds index.

3.2 Representing tuples

We can’t merely store all the items of the tuple consecutively in memory; we need to know how many items there are. Accordingly, we’ll add a header word at the beginning of our tuple in memory, that will store the size of the tuple:

Note carefully that the first word is an actual integer; it is not an encoded value in our language.

Unlike pairs, when we allocate tuples we might easily violate our alignment invariant. In fact, simply allocating a pair will do so, because we now need three words in total: the header word plus the two component words. We can resolve this in one of two ways: we could either add a padding word at the end of our tuple to bring it back into alignment if necessary, or we could increment R15 once more to bring it back into alignment.

Do Now!
What are the possible tradeoffs of these two approaches? Are there any observable differences between them, given our language so far?

Again, we need to tag our tuple values, just as we did above for pairs. Since tuples generalize pairs, the simplest approach is to eliminate pairs as a special case, and just use tuples everywhere — and then reuse the 0x1 tag to now mean tuples. It’s important to note that we could use both representations in our compiler — but if we use two distinct representations, we need to use two different tag values to distinguish them!

Do Now!
What are the possible tradeoffs of using just one representation for all tuples, vs using two representations for pairs and tuples separately?

3.3 ANF transformations

We simply generalize:

type 'a cexpr =
  ...
  | CTuple of 'a immexpr list * 'a (* components of the tuple *)
  | CGetItem of 'a immexpr * int * 'a (* tuple, desired index *)

Exercise
Complete the ANF transformation for ETuple. Why doesn’t CTuple require the size of the tuple any more?

3.4 Compiling tuples and tuple accesses

Again we generalize, assuming that all parts of the tuple have been evaluated (as ensured by ANFing).

... assume the parts of the tuple are already evaluated ...
mov [R15 + 0],     n   ;; the size of the tuple
mov [R15 + 8 * 1], <first part of tuple>
mov [R15 + 8 * 2], <second part of tuple>
...
mov [R15 + 8 * n], <last part of tuple>
mov RAX, R15           ;; Start creating the tuple value itself
add RAX, 0x1           ;; tag the tuple
add R15, 8 * (n + 1)   ;; bump the heap pointer
add R15, (0 or 8)      ;; realign the heap pointer if needed

Exercise
Implement this in compile.

To implement a tuple access, again we generalize, being careful to account for the header word:

mov RAX, <the tuple value>
<check that RAX is indeed a tuple>
sub RAX, 0x1                 ;; untag it
cmp n, 0                     ;; \ make sure the index
jl  index_too_low            ;; / is non-negative
cmp n, [RAX]                 ;; \ make sure the index is
jge index_too_high           ;; / within the size of the tuple
mov RAX, [RAX + 8 * (n + 1)] ;; treat RAX as a pointer, and get its nth word

Exercise
Implement this in compile.

3.5 Type Checking and Type Inference

Do Now!
What goes wrong for type-checking and/or type-inference of general tuples?

This time, not only do we have trouble guessing the “other” component types during type-checking, but both type-checking and type-inference have trouble guessing the width of the tuple. This is because there is no type variable that says “I am a tuple of arbitrary width”, so inference cannot generate an appropriately constrained type variable.2The closest technique to handle this, called row polymorphism, is intended to handle records rather than tuples; this is why SML actually treats its tuples as records with fields whose “names” are integers. SML’s version of our tuple-accessor expressions are actually functions “named” #1, #2, etc. It is unclear to me whether this is a clever solution, or merely a hacky one.

Once again, type-checking will restrict itself to working with tuple-accesses where the expression is merely an identifier.

Type-inference can guess the size of the tuple, though, because our accessor specifies it: this is why our expressions said e[7 of 9], rather than just e[7]. We can then create a tuple of the appropriate size, whose components are all fresh type variables, and then continue type inference as needed:

\begin{equation*}\dfrac{\Gamma \vdash e_1 : \mathsf{\tau_1} \quad \cdots \quad \Gamma \vdash e_n : \mathsf{\tau_n}}{\Gamma \vdash (e_1, \ldots, e_n) : \mathsf{\tau_1 * \cdots * \tau_n}} \qquad\qquad \dfrac{\Gamma \vdash e : \mathsf{\tau_1 * \cdots * \tau_n}}{\Gamma \vdash e[i \operatorname{of} n] : \mathsf{\tau_i}} \end{equation*}

4 Generalized bindings

Now that we have larger tuples, we might well want to nest them within one another. The accessor syntax quickly gets cumbersome to use, though. Perhaps we can take inspiration from ML, and allow more complex bindings in our let expressions, to bind names to all the parts of a tuple at once.

We’ll write a new pass for our compiler that desugars3It’s often subjective where to draw the line between “syntactic sugar” and “new feature”: formally, after all, beyond a certain point all languages are equally expressive! My sense of the distinction is that, if a feature can easily be translated from one concrete syntactic form to another, where the transformation mostly just rearranges existing expressions rather than rewrites them heavily, then we consider it “syntactic sugar.” Under this measure, transforming sequencing into let-bindings counts as sugar, but ANF transformations do not. our input program into an equivalent, more verbose form:

let (x, y, z) = (4, 5, 6) in x + y + z

===> desugars to ===>

let temp = (4, 5, 6) in
let x = temp[0 of 3] in
let y = temp[1 of 3] in
let z = temp[2 of 3] in
x + y + z

Do Now!
The temp name is not present in the original program, nor are the numbers 0, 1, 2 or 3. Where did they all comefrom?

This pass must recur throughout the program, as all of our passes do, and rewrite any sequence expressions it encounters. The advantage of this approach is that our subsequent passes can completely ignore the new sequencing expression form (they can throw an InternalCompilerException instead), and therefore no other part of our language is affected.

5 Tuples and Memory Allocation

If we’re using R15 to store the memory address where our available heap space begins, where do we get its initial value from?

main.c uses malloc (or calloc) to preallocate a large region of memory that we can use in our programs. But where does malloc know where available memory begins? We don’t pass malloc a starting address, so the start address isn’t on the stack. And we’ve accounted for the purposes of all the available registers, so it’s not hiding in a register (the way that we’re using R15).
The implementation of malloc stores several pointers that maintain a clever structure of free and allocated chunks of memory, divided among arenas of allocations of similar sizes. But where can those pointers live? They can’t be on the heap itself, since they help manage the heap!
Instead, we need to store those pointers in some well-known, statically known location.
Before, when introducing stacks, we had a simple memory-layout diagram that looked like this:
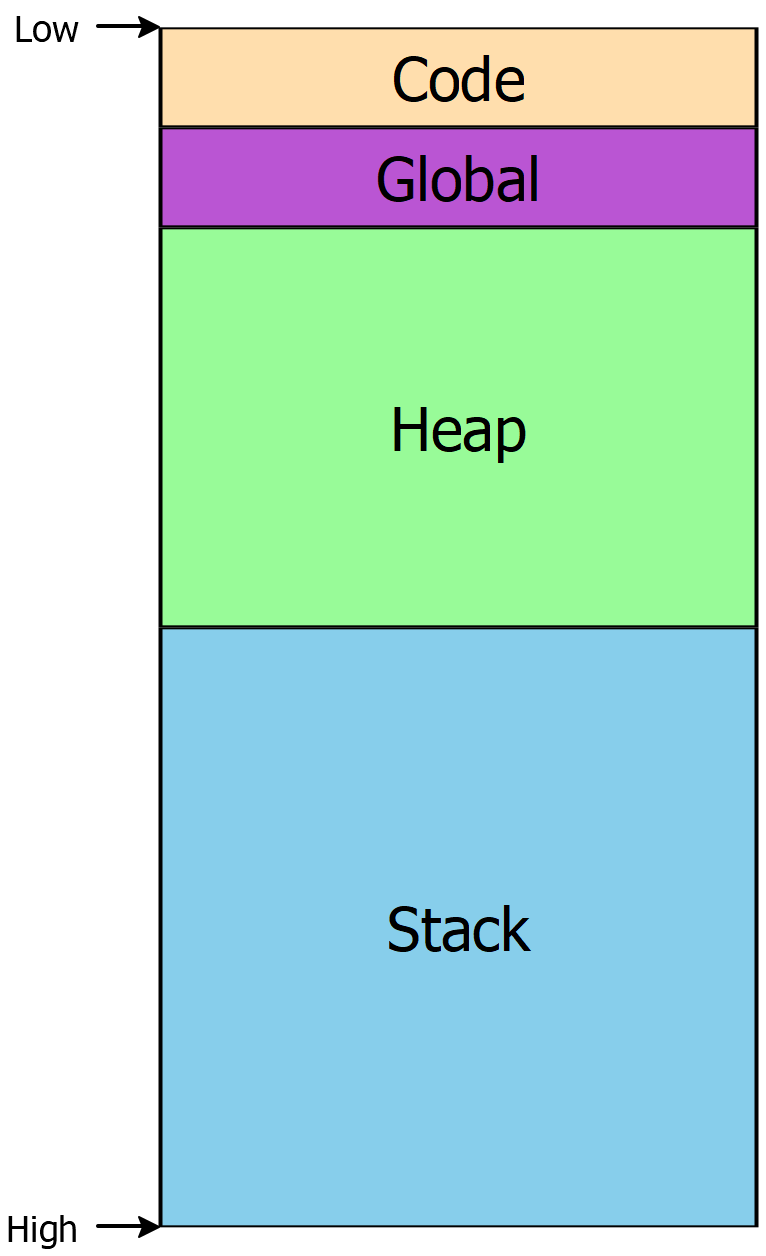
This is a bit simplistic – particularly that “Global” section. What goes in there? Among other things, that section breaks down into smaller sections, with various purposes:
- The .data section includes global constants known at compile-time
- The .bss section includes global names whose values aren’t known (and so are initialized to zero)
- The .tdata and .tbss sections are analogous to .data and .bss sections, but are thread-local
Crucially, the addresses of these four sections are constant, determined by the linker when the executable is produced, and their sizes are known statically: they’re not part of the heap, and any variables stored within them are stored at predictable locations. So the implementation of malloc ultimately relies on a thread-local variable, stored in the .tbss section and initialized as part of the startup of the program before main() ever gets called, to hold the pointer to the first arena.
Walking our way back up the list above: since the address of the pointer to the first arena is statically known, it doesn’t need to be passed in via a function parameter, or via a register; it’s now possible for malloc to correctly provide us with unique, newly-allocated regions of memory, which we can then use in our programs with impunity.

1Multiples of 8 are actually guaranteed for us, but it is worthwhile to ensure this for ourselves, especially if for some reason we need a more stringent alignment guarantee later on.

2The closest technique to handle this, called row polymorphism, is intended to handle records rather than tuples; this is why SML actually treats its tuples as records with fields whose “names” are integers. SML’s version of our tuple-accessor expressions are actually functions “named” #1, #2, etc. It is unclear to me whether this is a clever solution, or merely a hacky one.

3It’s often subjective where to draw the line between “syntactic sugar” and “new feature”: formally, after all, beyond a certain point all languages are equally expressive! My sense of the distinction is that, if a feature can easily be translated from one concrete syntactic form to another, where the transformation mostly just rearranges existing expressions rather than rewrites them heavily, then we consider it “syntactic sugar.” Under this measure, transforming sequencing into let-bindings counts as sugar, but ANF transformations do not.

1	Computing with arbitrary-sized data
2	Adding pairs to our language
3	Generalizing to tuples
4	Generalized bindings
5	Tuples and Memory Allocation