Lecture 10: Proper Tail Calls on x64
This is the counterpart to Lecture 9, using the x64 calling convention instead of the stack-only calling convention. Most of the material is the same, so we focus primarily on the stack-layout diagrams and on the details of the tail-calling code itself.
1 Examining the stack
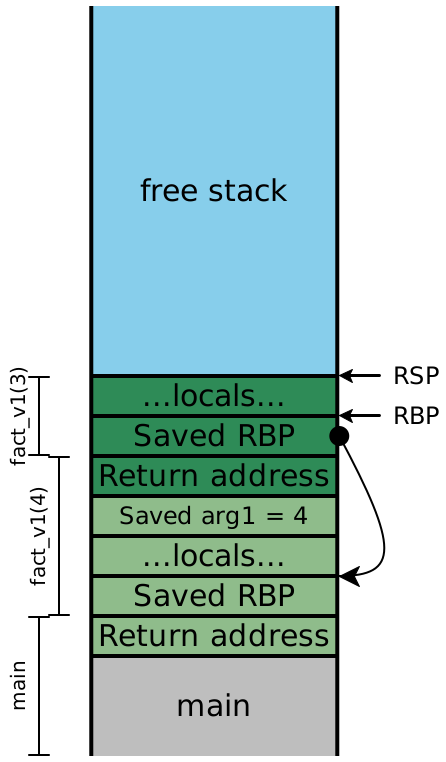
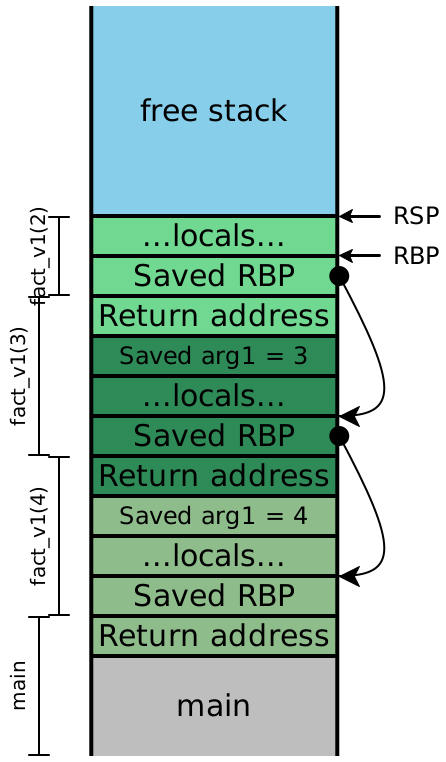
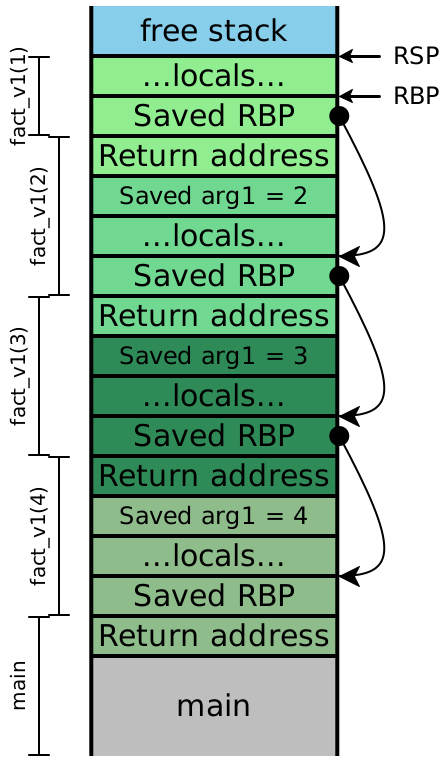
Let’s consider what the stack looks like while evaluating
fact_v1. (As before, in this diagram, colors indicate which stack frame
uses a particular value on the stack, while the brackets indicate which stack
frame created a particular value on the stack.)
In top-level |
| In |
| In |
| In |
| In |
At |
| At |
| At |
| At |
| About to return |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Note: The example code above uses functions with only one argument, so
no function arguments ever got pushed onto the stack for a given function
call. However, the first argument to our functions is passed in
RDI, which is a caller-saved register that is going to be needed after
the call returns: it needs to be saved (onto the stack) before each function
call so that it can be restored and used afterward. In general, with
larger-arity functions, our stack picture will contain arguments 7 and up,
spliced in between the “Saved arg1” slot of one stack frame and the “Return
address” slot of the next stack frame. Additionally, our diagram only tracks
the value of RDI; if the functions needed more arguments, we’d need to
keep track of the remaining argument registers (RSI, RDX,
RCX, R8 and R9), and we’d need to save those values onto the
stack as well. The specific order of the saved arguments on the stack doesn’t
matter; we just need to pick a location for each saved value and be consistent
about it.
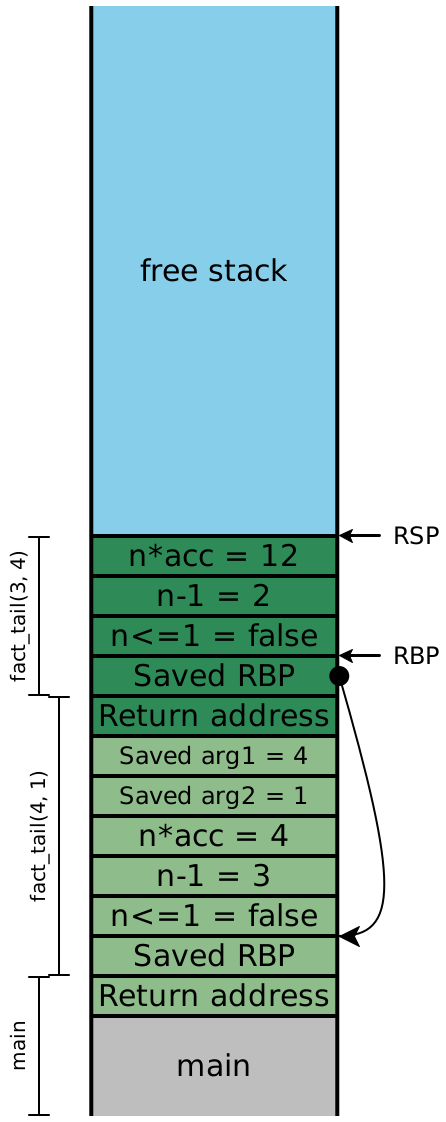
Now let’s examine the stacks for fact_v2, assuming we compile our
code exactly as we’ve always been. We’ll include the local variables, this time:
In top-level |
| In |
| In |
| In |
| In |
At |
| At |
| At |
| At |
| About to return |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Because the recursive calls here are all in tail-position, the next four
instructions are all going to be ret instructions, which means the
entirety of this stack can effectively be eliminated in one step. In other
words, once the olive stack frame makes the call to the dark green frame,
we never need to access an olive stack slot again —RDI and RSI aren’t needed. Looking carefully
at the stack, we see that the next values for n and
acc are precisely the local values computed in the
previous stack frame, and moreover, each stack frame has exactly the
same shape. If instead of creating a new stack frame, we simply
reused the existing one, then we wouldn’t need more than constant
stack depth to provide arbitrary call depth!
2 Strategy (for fewer than 7 arguments)
Rather than saving RDI and RSI before each call by pushing
them onto the stack, we can elide that step, and just overwrite their values
with the new argument values. Once we’ve done that, we need to re-enter
our existing function, but we can’t use call to do it.
Do Now!
Why not?
The meaning of call is to push a return address onto the stack and jump
to the destination address. But we already have the necessary return address
sitting on the stack! We also have a saved RBP on the stack too, which
means that the function prologue we normally execute isn’t really needed here.
So instead, we’ll simply jump directly to the next instruction in our
code. The compiled assembly for fact_tail would then look
roughly like this (ignoring all tag checks, and simplifying the code
slightly):
fact_tail:
fact_tail_prologue:
push RBP
mov RBP, RSP
sub RSP, 16 ; reserve stack slots
fact_tail_body:
mov RAX, RDI ; load n
cmp RAX, 2 ; compare to representation of 1
jg keep_going
mov RAX, RSI ; load acc into answer
mov RSP, RBP ; and return directly
pop RBP ; to the original
ret ; caller
keep_going:
mov RAX, RDI ; \
sub RAX, 2 ; | compute n - 1
mov [RBP - 8], RAX ; /
mov RAX, RDI ; \
sar RAX, 1 ; |
imul RAX, RSI ; | compute n * acc
mov [RBP - 16], RAX ; /
mov RAX, [RBP - 8] ; \
mov RDI, RAX ; / OVERWRITE argument n
mov RAX, [RBP - 16] ; \
mov RSI, RAX ; / OVERWRITE argument acc
jmp fact_tail_body ; AND RESTART fact_tailThis code is almost legible enough that we could turn it into C code pretty easily:
int fact_tail(int n, int acc) {
while (true) {
if (n <= 1) { return acc; }
else {
int temp1 = n - 1;
int temp2 = n * acc;
n = temp1;
acc = temp2;
}
}
}We’ve turned our (tail-)recursive function into a while-loop, and eliminated all the function calls!
3 Implementation pitfalls
3.1 Reusing arguments
Consider the following code:
def max(x, y):
if y >= x: y
else: max(y, x)This is clearly tail-recursive, so we can apply the same technique above.
Since we have no intermediate expressions (again, simplifying the conditional),
we don’t even need to move RSP at all; all our values are already on the stack:
max:
max_prologue:
push RBP
mov RBP, RSP
max_body:
mov RAX, RSI ; load y
cmp RAX, RDI ; compare to x
jl keep_going
mov RAX, RSI ; load y into answer
mov RSP, RBP ; and return directly
pop RBP ; to the original
ret ; caller
keep_going:
mov RAX, RSI ; \
mov RDI, RAX ; / OVERWRITE argument x
mov RAX, RDI ; \
mov RSI, RAX ; / OVERWRITE argument y
jmp max_body ; AND RESTART maxDo Now!
What went horribly wrong?
Exercise
Try to fix it.
Try tracing through two simple calls to max, to test both
branches of the if expression, and carefully step through the
generated assembly. If we call max(10, 20), then we fall through
the jl instruction, and end up returning RSI, which is
y as expected. But suppose we try max(20, 10).
then we fall through to keep_going, where we load the current value of
RSI and overwrite RDI with it, which effectively
copies y into x. Then we load the current value of
RDI and copy it into RSI, in an attempt to copy the
current value of x into y —x is gone! So the effect of our tail-call of
max(y, x) is to call (10, 10), which then executes
the first branch of the conditional and returns 10.
(Note that if we updated our arguments in the other order, such that we
overwrote y before we overwrote x, we would have an
even more insidious problem: This particular function would compute the correct
answer! Our call to max(10, 20) would effectively call
max(20, 20) and return 20 —
The problem is that our new arguments to the call reside in locations that we
are about to overwrite, and we’ve managed to create a cycle from the
location of y, to the value of the
new argument of x, to the location of x to
the value of the new argument of y. Our naive strategy of
simply moving arguments was too simple. Instead, we can try any of the
following strategies in increasing sophistication (or others, in a similar spirit):
At the beginning of every function, just copy all the arguments into new local variables, and then never use the arguments directly again. This ensures that we can’t have cycles, as above, so our tail calls will always work. On the other hand, we’ll use twice as much stack space as needed.
Before every tail call,
pushall the new argument values onto the stack, thenpopthem (in the opposite order) into their correct locations. This is safe, but every tail call temporarily uses a bit more stack space than is necessary.Check whether any of the argument values come from locations that we’re about to overwrite. If so, use the
push/popapproach above; if not, use the simplermovapproach.Check whether there exists a cycle between new argument values and their locations, as in this
maxexample. For each cycle, break the cycle by pushing one value onto the stack, thenmovthe remaining arguments as needed, thenpopthe last argument of the cycle into its place. For any other arguments, justmovthem as needed.
The last strategy above is optimal: it never uses more that one extra stack
slot at a time, and it uses the minimum number of movs and stack
operations. But it’s also clearly the most complicated, and therefore the
hardest to test and guarantee correct. The next-to-last strategy strikes a
good balance between efficiency and simplicity: the safety condition is easy to
check, and both the push/pop-based code and the mov-based
code handle all arguments in a uniform manner, making it much easier to test.
3.2 Changing arities
The technique above is not limited to self-recursion; it works for tail-calls between functions as well, meaning that mutually recursive functions can also be compiled to essentially a while-loop with a few conditions inside it.
However, the technique above works smoothly only for tail calls to callees whose
arities are no greater than their callers’ arities. Suppose function
F calls function G, whose arity is \(A_G\).
Suppose G then tail-calls another function H with arity
\(A_H > A_G\). We have two problems:
First, there isn’t enough room to replace the existing arguments with the intended new ones. We’d need to shift the saved
RBPand return address up by a few stack slots, which themselves might be in use (those might well be the new argument values we want to use!), so we’d have to move them as well. This could easily get expensive.Second, and more importantly, consider what happens when
Hfinally returns toF(note:Gis no longer present; that’s the point of a tail call).Fwill pop off the \(A_G\) arguments it pushed onto the stack...but there are actually now \(A_H\) arguments, and soRSPwill wind up in the wrong place! In other words, the calling convention we’ve described so far is incapable of supporting tail-calls to greater-arity functions.
Obviously, these difficulties are not insurmountable, but they do require some clever thought...