Assignment 6: Egg-eater: Tuples
Due: Fri 2/28 at 11:59pm
git clone
In this assignment you’ll extend Diamondback to implement mutable tuples, whose syntax looks vaguely egg-shaped, if you don’t think about it too much...
(egg)1 Language and Requirements
Egg-eater starts with the same semantics as Diamondback, and adds support for
tuple expressions: creating values, accessing components, and mutating components
sequencing of expressions
simple recursive tuples, with
nilvaluesricher binding syntax
The runtime system must add support for
Allocating values on the heap, and avoiding heap overflows
Printing tuple values
Comparing tuple values for structural equality
Asking the user for input
This is a large assignment, and its pieces are tightly interconnected. Read through the whole assignment below carefully, then take note of the recommended TODO list at the bottom for a suggested order to tackle these pieces.
2 Syntax Additions and Semantics
The main addition in Egg-eater is tuple expressions, along with accessor
expressions for getting or setting the contents of tuples, and a unary
primitive for checking if a value is a tuple. Tuple expressions are a series
of zero or more comma-separated expressions enclosed in parentheses.
(The syntax of one-element tuples is slightly odd, and requires a trailing
comma; this is to avoid confusion with our existing use of parentheses for
grouping infix expressions.) A tuple access expression is an expression
followed by an expression enclosed in square brackets, which expresses
which field to be accessed. Finally, istuple is a primitive (like
isnum and isbool) that checks for tuple-ness.
‹expr› ... ‹tuple› ‹tuple-get› ‹tuple-set› istuple ( ‹expr› ) ‹expr› ; ‹expr› let ‹bindings› in ‹expr› ‹tuple› ( ) ( ‹expr› , ) ( ‹expr› , ‹expr› , ... ‹expr› ) ‹tuple-get› ‹expr› [ ‹expr› ] ‹tuple-set› ‹tuple-get› := ‹expr› ‹bindings› ‹bind› = ‹expr› ‹bind› = ‹expr› , ‹bindings› ‹bind› ... _ IDENTIFIER ( ‹binds› ) ‹binds› ‹bind› ‹bind› , ‹binds›
In case there’s ambiguity with e.g. tuple set operations, you may need to parenthesize the expression on the right-hand side (the new value at that tuple slot).
For example, we can create three tuples and access their fields:
let unit = () in
let one = (1,) in
let three = (3, 4, 5) in
three[0]A tuple-set expression evaluates its arguments, updates the tuple at the appropriate index, and returns the new value at that index as the result. For instance, we can write
let three = (0, 0, 0) in
let three1 = three[0] := 1 in
let three2 = three[1] := 2 in
three[2] := 3;
# Now three equals (1, 2, 3), three1 == 1 and three2 == 2
let pair = (5, 6) in
pair[1] := three[1] := 10
# Now three equals (1, 10, 3) and pair equals (5, 10)We can use other expressions for tuples and tuple accessors than just identifiers and numbers:
let tup = ((1, 2, 3), 4) in
tup[1][2] := 5;
(1, 2, 3, 4)[0 + 1] := isbool(5)Lastly, we can actively destructure tuples when we bind them:
let t = (3, ((4, true), 5)) in
let (x, (y, z)) = t
x + y[0] + zNotice that we can destructure tuples “all the way down”, or “stop early”:
in this case, y is bound to the tuple (4, true), or
said another way, y == t[1][0].
In the expr datatype, these are represented as:
type 'a expr =
...
| ETuple of 'a expr list * 'a
| EGetItem of 'a expr * 'a expr * 'a
| ESetItem of 'a expr * 'a expr * 'a expr * 'a
| ESeq of 'a expr * 'a expr * 'a
type prim1 =
...
| IsTupleIn ANF syntax, these expressions are represented as cexprs, with immexpr
components:
type 'a cexpr =
...
| CTuple of 'a immexpr list * 'a
| CGetItem of 'a immexpr * 'a immexpr * 'a
| CSetItem of 'a immexpr * 'a immexpr * 'a immexpr * 'aNote that these expressions are all cexprs, and not immexprs – the allocation
of a tuple counts as a “step” of execution, and so they are not themselves already
values.
To make the bindings work in our AST, we need to enhance our representation of binding positions:
type 'a bind =
| BName of string * 'a
| BTuple of 'a bind list * 'a
| BBlank of 'a
type 'a binding = ('a bind * 'a expr * 'a)
type 'a expr = ...
| ELet of 'a binding list * 'a expr ' a
type 'a decl =
| DFun of string * 'a bind list * 'a expr * 'aLet-bindings now can take an arbitrary, deeply-structured binding, rather than
just simple names. Further, because we have mutation of tuples, these act more
like statements than expressions, and so we may need to sequence multiple
expressions together. Further still, sequencing of expressions acts just like
let-binding the first expression and then ignoring its result, before executing
the second expression. In other words, e1 ; e2 means the same
thing as let _ = e1 in e2. To avoid making up a new name for the
ignored value, we introduce BBlank bindings that indicate the programmer
doesn’t need to store this value in a variable. Lastly, now that we have
richer binding structure, we’re going to use it everywhere, including in
function definitions:
def add-pairs((x1, y1), (x2, y2)):
(x1 + x2, y1 + y2)This should be treated as syntactic sugar for a similar function
def add_pairs(p1, p2):
let (x1, y1) = p1, (x2, y2) = p2 in
(x1 + x2, y1 + y2)(Your solution will likely generate different names than p1 or
p2.)
3 Desugaring away unnecessary complexity
The introduction of destructuring let-bindings, sequencing, and blanks all make the rest of compilation complicated. ANF’ing, stack-slot allocation, and compilation all are affected. We can translate this mess away, though, and avoid dealing with it further.
Nested let-bindings: Given a binding
let (b1, b2, ..., bn) = e in bodywe can replace this entire expression with the simpler but more verbose
let temp_name1 = e,
b1 = temp_name1[0],
b2 = temp_name1[1],
...,
bn = temp_name1[(n-1)]
in body(Note that the (n-1) in the last binding is not an
expression, but a compile-time constant literal integer, deduced solely from
the length of the original binding expression.)
Nested function-argument bindings: Function arguments can now be nested
bindings as well. The desugaring above almost works, except there’s no
explicit e expression to bind to the tuple. Instead, you should
generate a temporary argument name, and treat the argument bindings as being
bound to those. The example of add_pairs above gives the
intuition: it wraps the existing body of the function in these new
let-bindings, which reduces the problem to solving nested let-bindings.
Sequences:
You should implement a desugar phase of the compiler, which runs somewhere
early in the pipeline and which makes subsequent phases easier, by implementing
the translations described in this section.
Be sure to leave comments (near your compile_to_string pipeline)
explaining (1) why you chose the particular ordering of desguaring
relative to the other phases that you did, and (2) what syntactic
invariants each phase of your compiler expects. You may want to enforce those
invariants by throwing InternalCompilerErrors if they’re violated.
4 Semantics and Representation of Tuples
4.1 Tuple Heap Layout
Tuples expressions should evaluate their sub-expressions in order from left to right, and store the resulting values on the heap. We discussed several possible representations in class for laying out tuples on the heap; the one you should use for this assignment is:

That is, one word is used to store the count of the number of elements in the tuple, and the subsequent words are used to store the values themselves. Note that the count is an actual integer; it is not an encoded Egg-eater integer value.
A tuple value is stored in variables and registers as the address of the
first word in the tuple’s memory, but with an additional 1 added to the value
to act as a tag. So, for example, if the start address of the above memory
were 0x0adadadadadadad0, the tuple value would be 0x0adadadadadadad1. With this change, we
extend the set of tag bits to the following:
Numbers:
0in the least significant bitBooleans:
111in the three least significant bitsTuples:
001in the three least significant bits
Visualized differently, the value layout is:
Bit pattern |
| Value type |
|
| Number |
|
| True |
|
| False |
|
| Tuple |
Where W is a “wildcard” nibble and w is a “wildcard” bit.
4.2 Accessing Tuple Contents
In a tuple access expression, like
let t = (6, 7, 8, 9) in t[1]The behavior should be:
Evaluate the expression in tuple position (before the brackets), then the index expression (the one inside the brackets).
Check that the tuple position’s value is actually a tuple, and signal an error containing
"expected tuple"if not.Check that the index number is a valid index for the tuple value —
that is, it is between 0and the stored number of elements in the tuple minus one. Signal an error containing"index too small"or"index too large"as appropriate.Evaluate to the tuple element at the specified index.
You can do this with just RAX, but it causes some minor pain. The register
R11 is in assembly.ml —RAX and R11 in this case (for example saving the index in R11 and using
RAX to store the address of the tuple). This can save a number of instructions.
Note that we will generate code that doesn’t need to use R11 or RAX beyond
the extent of this one expression, so there is no need to worry about saving or restoring
the old value from R11.
You also may want to use an extended syntax for mov in order to combine these
values for lookup. For example, this kind of arithmetic is allowed inside
mov instructions:
mov RAX, [RAX + R11 * 8]This would access the memory at the location of RAX, offset by the value of
R11 * 8. So if the value in R11 were, say 2, this may be part
of a scheme for accessing the first element of a tuple (there are other details
you should think through here; this is not a complete solution) Feel free to
add additional arg types in assembly.ml to support a broader range of
mov instructions, if it helps.
Neither R11 nor anything beyond the typical RegOffset is required to make
this work, but you may find it interesting to try different shapes of
generated instructions.
4.3 General Heap Layout
The register R15 has been designated as the heap pointer. The provided
main.c does a large malloc call, and passes in the resulting address as an
argument to our_code_starts_here. The support code provided fetches this
value (as a traditional argument), and stores it in R15. It also does a bit
of arithmetic to make sure that R15 starts at a 16-byte boundary —R15 are 0b0000. It is up to your code to ensure that:
The value of
R15always ends in0b0000. This ensures that the beginning of each allocation happens at a 16-byte boundary, which means that we only need 60 bits of a 64-bit word in order to store addresses. The least significant bits are then fair game for the tag. At the moment, we only need three bits for tagging purposes, but to leave room for future growth (and to practice the necessary techniques), we’ll proactively ensure a fourth bit is already available if we need it.The value of
R15is always the address of the next block of free space (in increasing address order) in the provided block of memory.
The first point above means that for tuples that take up an odd amount of
8-byte words, R15 needs to leave some “dead space” in order to align with a
16-byte boundary. For example, assume before an allocation R15 is pointing at
address 0x000000000000ada0:
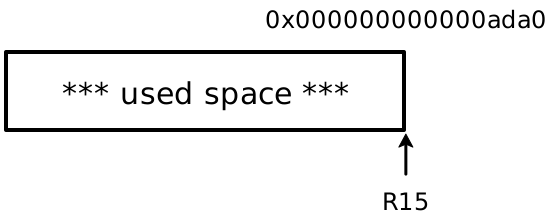
And then we need to allocate the tuple (4, true). Since we need one word for
the size (2) and one word each for the two values 4 and true, there are 3
words required to store the tuple. If we left the heap in this state:

Our heap pointer is 8-byte aligned, but is not 16-byte aligned: the address
ends in 0x8, so the fourth bit is non-zero and can’t be used as a tag bit
(if it ever becomes necessary). So instead of the above resulting picture,
R15 should be moved one word further:

The padding is unused space to make the heap allocation strategy with tagging
work cleanly —
4.4 Interaction with Existing Features
Any time we add a new feature to a language, we need to consider its interactions with all the existing features. In the case of Egg-eater, that means considering:
If expressions
Function calls and definitions
Tuples in binary and unary operators
Let bindings
We’ll take them one at a time.
If expressions: Since we’ve decided to only allow booleans in conditional position, we simply need to make sure our existing checks for boolean-tagged values in if continue to work for tuples.
Function calls and definitions: Tuple values behave just like other values when passed to and returned from functions —
the tuple value is just a (tagged) address that takes up a single word. Tuples in let bindings: As with function calls and returns, tuple values take up a single word and act just like other values in let bindings.
Tuples in binary operators: The arithmetic expressions should continue to only allow numbers, and signal errors on tuple values. There is one binary operator that doesn’t check its types, however:
==. We need to decide what the behavior of==is on two tuple values. Note that we have a (rather important) choice here. Clearly, this program should evaluate totrue:let t = (4, 5) in t == tHowever, we need to decide if
(4,5) == (4,5)should evaluate to
trueorfalse. That is, do we check if the tuple addresses are the same to determine equality, or if the tuple contents are the same. For this assignment, we’ll take the somewhat simpler route and compare addresses of tuples, so the second test should evaluate tofalse.However, providing a structural equality operation, where we check the tuple’s contents (recursively, if needed), is also useful. For this, write a two-argument function
equalinmain.cthat handles this. Provide this function as one of the built-in functions available in the global scope of Egg-eater programs. (Note that this does not mean thatequalshould be added as a newPrim2!) Yourequalfunction should work on all acyclic tuples of moderate depth, but does not have to be robust in the presence of cycles or overflowing the C stack.Tuples in unary operators: The behavior of the unary operators is straightforward, with the exception that we need to implement
printfor tuples. We could just print the address, but that would be somewhat unsatisfying. Instead, we should recursively print the tuple contents, so that the programprint((4, (true, 3)))actually prints the string
"(4, (true, 3))". This will require some careful work with pointers inmain.c. A useful hint is to create a recursive helper function forprintthat traverses the nested structure of tuples and prints single values. Again, yourprintfunction should work properly for all acyclic tuples of reasonable depth, but does not have to be robust in the presence of cycles or overflowing the C stack.
5 Approaching Reality
With the addition of tuples, Egg-eater is dangerously close to a useful
language. Of course, it still puts no control on memory limits, doesn’t have a
module system, and has other major holes. However, since we have structured
data, we can now, for instance, implement a linked list. We need to pick a
value to represent empty. Since our tuples are heap-allocated,
let’s make the same
billion
dollar mistake that Sir Tony Hoare made, and create a nil value.
Then we can write link, which creates a pair of the first with the
next link:
def link(first, rest):
(first, rest)
let mylist = link(1, link(2, link(3, nil))) in
mylist[0]Now we can write some list functions:
def length(l):
if l == nil: 0
else:
1 + length(l[1])Try building on this idea, and writing up a basic list library. Write at least
sum, to add up a numeric list, append, which
concatenates two lists, and reverse, which reverses a list. Hand
them in in a file in the input/ directory called lists.egg.
Remember that make output/lists.run will build the executable for this
file.
Write more functions if you want, as well, and test them out.
6 Wait, nil??
We have to amend our tuple operations above, to be sure they cannot cause a segmentation fault and access undefined memory. Accordingly:
Represent
nilat runtime with a tuple-tagged value that is obviously an invalid memory address. The address0x0will do nicely, since it’s guaranteed not to be an address in our runtime-allocated heap.Enhance the tuple-get and tuple-set expressions to reject accessing the fields of
nil, and signal an error containing"access component of nil".Ensure that your
printruntime function does not crash when given data containingnil.
7 Recommended TODO List
Implement the
ETuple,EGetItemandESetItemcases in ANF. These should be relatively similar in structure to the other arbitrary-arity expression form,EApp...Get tuple creation and access working for tuples containing two elements, testing as you go. This is very similar to the pairs code from lecture.
Modify the binary and unary operators to handle tuples appropriately (it may be useful to skip
printat first). Test as you go.Make tuple creation and access work for tuples of any size. Test as you go.
Tackle
printfor tuples if you haven’t already. Test as you go. Reimplementprintas a global function provided from C, rather than as a built-inprim1.Implement
input, a C function that prompts the user for simple input —i.e., numbers or booleans; no need to write your own tuple parser in C! — and returns it to the running program. Provide this function as a globally-available function in Egg-eater. For example, print(input())should echo back whatever value the user entered.Write some list library functions (at least the three above) to really stress your tuple implementation. Rejoice in your implementation of the core features needed for nontrivial computation. (Well, aside from the pesky issue of running out of memory. More on that in lecture soon.)
Implement content-equality for all data (including tuples) as a runtime function
equal, and provide it as a globally-available function in Egg-eater.Try implementing something more ambitious than lists, like a binary search tree, in Egg-eater. This last point is ungraded, but quite rewarding!
A note on support code —
8 List of Deliverables
all your modified files (
compile.ml,pretty.mlor anything else)tests in an OUnit test module (
test.ml)any test input programs (
input/*/*.eggfiles), including at leastlists.egg
Again, please ensure the makefile builds your code properly. The black-box tests will give you an automatic 0 if they cannot compile your code!
DO NOT SUBMIT YOUR .git DIRECTORY! For that matter, don’t submit
your output or _build directories.
9 Grading Standards
For this assignment, you will be graded on
Whether your code implements the specification (functional correctness),
the clarity and cleanliness of your code, and
the comprehensiveness of your test coverage
10 Submission
Wait! Please read the assignment again and verify that you have not forgotten anything!
Please submit your homework to https://handins.khoury.northeastern.edu/ by the above deadline.
