Computer Graphics (CS4300) 2011S: Lecture 2
Today
- HW1 due today, HW2,3 assigned
- coordinate frames
- segments, rays, and intersections 2D
Coordinate Frames
- components of an
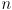 -dimensional vector
-dimensional vector 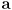 define a point
define a point  in an
in an 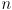 -dimensional coordinate frame as a linear combination of the
-dimensional coordinate frame as a linear combination of the 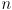
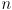 -dimensional basis vectors
-dimensional basis vectors 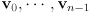 defining the frame
defining the frame - linear combination is computed as
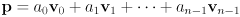
- same as product of a matrix and a vector:
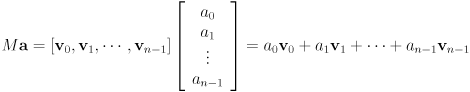
- (general
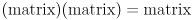 multiplication and its uses in graphics will be covered later in the course)
multiplication and its uses in graphics will be covered later in the course) - technically, any set of
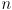
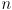 -dimensional vectors can form a basis for an
-dimensional vectors can form a basis for an 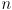 -dimensional frame as long as they are linearly independent
-dimensional frame as long as they are linearly independent - orthonormal bases are of particular interest: all
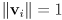 and for all
and for all 

- an orthonormal basis defines a Cartesian frame
- “standard” basis is
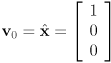
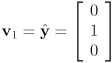
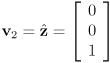 , so
, so 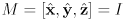
- note this is right-handed; if we had defined
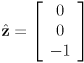 instead, it would have been left handed
instead, it would have been left handed - there are always exactly two options for the “handedness” (chirality) of a 3D orthonormal basis
- right-handed coordinate frames are typical in graphics, but not totally universal
- it is often useful to define other local coordinate frames with arbitrary pose relative to the standard global frame
- pose of an object is its position plus its orientation
- we will cover this more formally later, but basically, the pose of a local frame is defined by the location of its origin
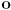 and an orthonormal basis
and an orthonormal basis 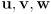
- all of these are vectors in the global frame
- the matrix
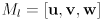 defines the orientation of the local frame
defines the orientation of the local frame - to transform a vector
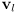 from the local to the global frame, compute
from the local to the global frame, compute 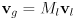
- note this does not change the magnitude of the vector, only its direction
- this is because the columns of
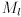 are orthonormal
are orthonormal
- since a vector is technically only a magnitude and a direction, with no specific “place in space”, no need for
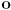 in this operation
in this operation - to transform a point or location
 from the local to the global frame, compute
from the local to the global frame, compute 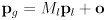
- going the other way: to transform a vector
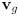 from the global to the local frame, compute
from the global to the local frame, compute 
- this uses the fact that the inverse of an orthogonal matrix is its transpose (show easy derivation from above eqn for
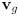 )
) - note this is the same as computing
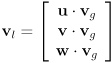 , as in the text
, as in the text
- transforming a point or location
 from the global to the local frame: solve above
from the global to the local frame: solve above  eqn for
eqn for 
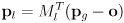
- note this is not the same as
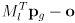
- there are algorithms to “square” up a set of vectors to ensure they are orthonormal
- also sometimes required to construct a basis given only two or one vector
- if given two non-parallel vectors, use cross product to produce third, and square up if necessary
- if given only one vector, first find some other non-parallel vector, then proceed as above
Rays and Segments
- points have already been discussed: an
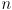 -dimensional vector can be used to represent a point in
-dimensional vector can be used to represent a point in 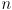 dimensions by giving a displacement relative to the origin in some coordinate frame
dimensions by giving a displacement relative to the origin in some coordinate frame - a ray is a continuum of points starting at some location and continuing in a straight line to infinity
- can be represented as a start point
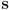 plus a unit vector
plus a unit vector 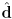 giving the direction of the ray
giving the direction of the ray - def works in any dimension
- a line segment, or just a segment, is the continuum of points along a straight line between two given locations
- usually represented as the two endpoints, typically identified as start
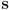 and end
and end 
- can also represent as start and a displacement
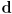 from there to end
from there to end- easy to convert:

- either def works in any dimension
- can define the “left” and “right” sides in 2D: stand at
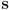 and face along
and face along 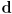
- on what side of the segment does a given point
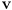 fall?
fall?- compute
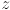 component of
component of 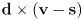 , extending each to 3D with
, extending each to 3D with 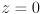 :
: 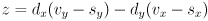
- this can also be written mathematically as
 ; the dot product with
; the dot product with 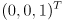 simply selects the
simply selects the 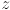 component of the result of the cross product. Don’t be confused by the transpose, that is there because we normally deal with column vectors, i.e.
component of the result of the cross product. Don’t be confused by the transpose, that is there because we normally deal with column vectors, i.e. 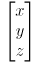 , not row vectors like
, not row vectors like 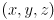 . But it would take a lot more vertical space to always type column vectors, so instead we usually type
. But it would take a lot more vertical space to always type column vectors, so instead we usually type 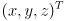 , since by definition
, since by definition 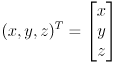 .
. - (note that
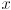 and
and 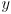 components of cross product of any two vectors each with
components of cross product of any two vectors each with 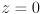 will be 0 anyway)
will be 0 anyway) - if positive,
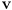 is on left of segment
is on left of segment - if zero,
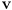 is coincident with line through segment
is coincident with line through segment - if negative,
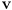 is on right of segment
is on right of segment - this can be used e.g. to pick triangles in the plane
- unit normal
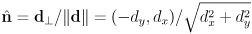 can also be used to answer this question (we will see this when studying line equations and the signed distance from a point to a line)
can also be used to answer this question (we will see this when studying line equations and the signed distance from a point to a line) - can parametrize points
 along the segment as
along the segment as 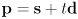 where
where 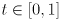
- intersection of two 2D segments:
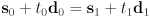
- two linear equations in two unknowns
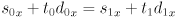
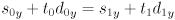
- rearranging into standard form,

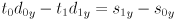
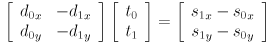
- can solve for
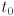 and
and 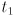 (carefully):
(carefully):- e.g. use Cramer’s rule, watch out for “no solution”
- same result can be derived using law of sines and cross product
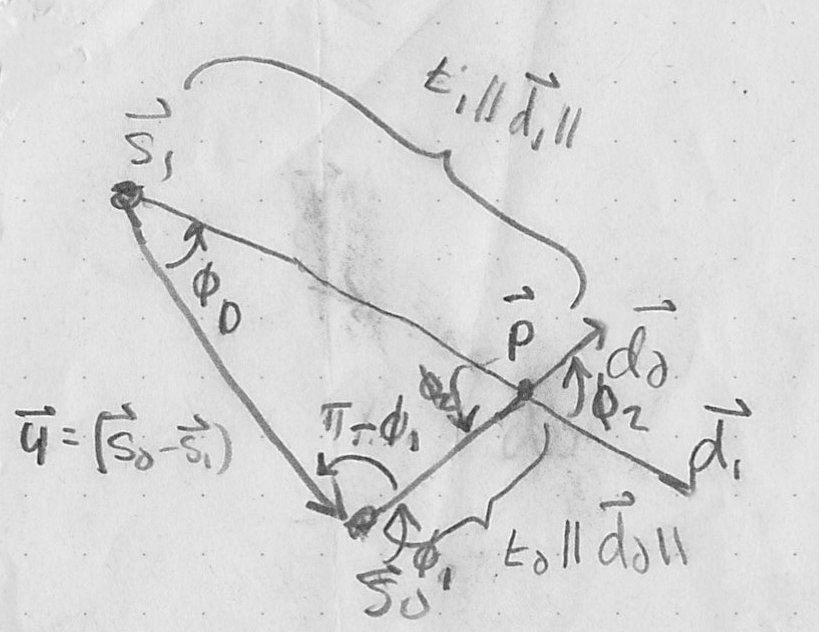
- let
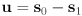
- law of sines:
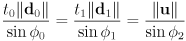
- treat
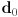 ,
, 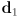 , and
, and 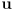 as 3D vectors with
as 3D vectors with 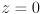
- the z-components of the cross products will thus have absolute value equal to the magnitude of the cross product, which is generally
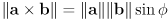 , where
, where 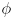 is the smaller counterclockwise positive angle between the two vectors, i.e. the angle measured counterclockwise either starting at
is the smaller counterclockwise positive angle between the two vectors, i.e. the angle measured counterclockwise either starting at 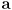 and ending at
and ending at 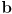 , or starting at
, or starting at 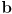 and ending at
and ending at 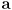 , whichever is smaller. Thus
, whichever is smaller. Thus 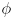 is generally always in the range
is generally always in the range 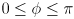 , and that makes
, and that makes 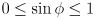 . However, the sign of the cross product z component in this case can be used to recover the original ccw angle specifically from
. However, the sign of the cross product z component in this case can be used to recover the original ccw angle specifically from 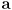 to
to 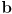 . This will be in the range
. This will be in the range 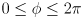 , which puts
, which puts 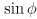 in the range
in the range 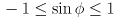 . That fact lets us compute
. That fact lets us compute 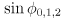 here as the
here as the 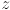 component of appropriate cross products. The angle will always be measured CCW from the first input vector to the cross product towards the second input, and it turns out that will make the signs correct for both intersecting and non-intersecting cases.
component of appropriate cross products. The angle will always be measured CCW from the first input vector to the cross product towards the second input, and it turns out that will make the signs correct for both intersecting and non-intersecting cases. - let
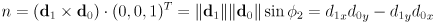
- let
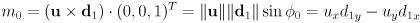
- let
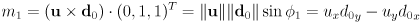
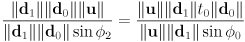
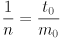
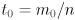
- similarly,
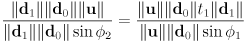
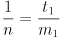
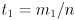
- if
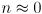 segments are collinear
segments are collinear - segments intersect iff
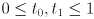
- same math works for segment/ray and ray/ray intersection, except the condition for the ray(s) is that
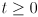
Next Time
- lines in 2D
- “triangle asteroids” example
- output devices
- reading on website
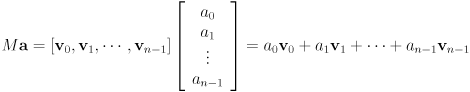
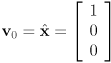
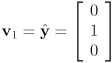
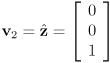 , so
, so 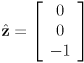 instead, it would have been left handed
instead, it would have been left handed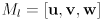 defines the orientation of the local frame
defines the orientation of the local frame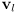 from the local to the global frame, compute
from the local to the global frame, compute 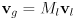
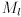 are orthonormal
are orthonormal in this operation
in this operation from the local to the global frame, compute
from the local to the global frame, compute 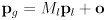
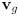 from the global to the local frame, compute
from the global to the local frame, compute 
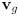 )
)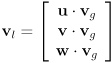 , as in the text
, as in the text from the global to the local frame: solve above
from the global to the local frame: solve above  eqn for
eqn for 
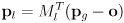
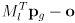
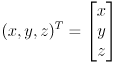 .
.