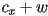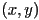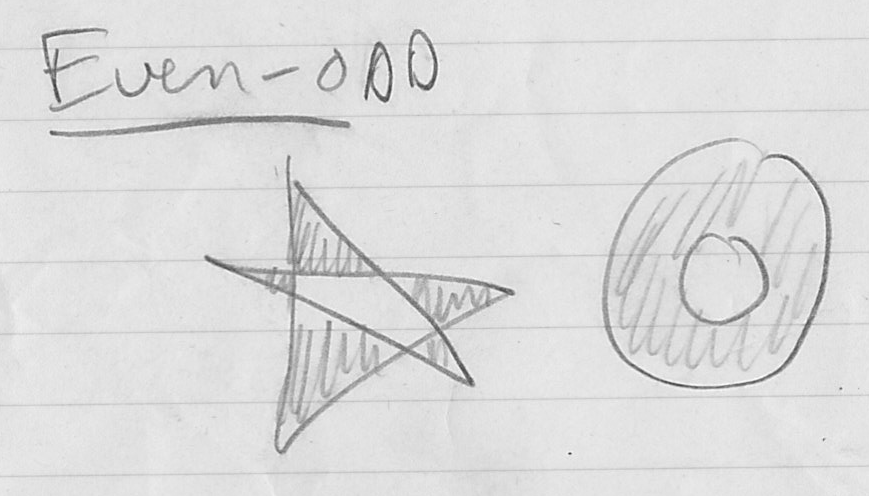Computer Graphics (CS 4300) 2010S: Lecture 8
Today
- HW1 graded and will return by email today
- HW2 due weds!
- finish from last time:
- Model-View-Controller (MVC) architecture
- common user interaction techniques
- rectangles in 2D
- polygons in 2D
- tessellation by ear-clipping
Rectangles in 2D
- axis-aligned rectangles are very common in 2D graphics, especially GUIs
- typically represented as a point
 giving the *upper left corner (i.e. the corner with minimum
giving the *upper left corner (i.e. the corner with minimum 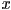 and
and  coordinates) plus (non-negative) width
coordinates) plus (non-negative) width 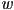 and height
and height 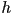 (horizontal and vertical extents, respectively)
(horizontal and vertical extents, respectively)
- often
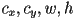 are all integers (pixel coords) but some APIs allow floating point rects as well
are all integers (pixel coords) but some APIs allow floating point rects as well - easy to check if a given point
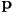 is in a rect:
is in a rect:  and
and 
- two axis-aligned rects
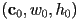 and
and 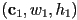 overlap iff
overlap iff - also easy to rasterize, e.g.
- for
 to
to 
- non-aligned rectangles are less common
- can treat as an axis-aligned in a rotated coordinate system (we will cover rotations in detail later this week)
- or, just don’t special-case, and handle like any other convex polygon
Polygons in 2D
- def: a simple polygon in 2D is an ordered sequence of line segments
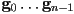 ,
,  , such that
, such that- each edge
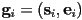 is the segment from a start vertex
is the segment from a start vertex 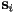 to an end vertex
to an end vertex 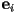
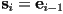 for
for 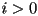
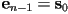
- non-adjacent edges do not intersect
- the only intersection of adjacent edges is at their shared vertex
- note that it is sufficient to store e.g. only the
 start vertices, and this also enforces the connectivity constraints by construction
start vertices, and this also enforces the connectivity constraints by construction - this also illustrates that the number of sides equals the number of vertices
- the polygon degenerates to a segment if
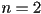 (it’s also possible to have degenerate polygons for
(it’s also possible to have degenerate polygons for 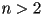 )
) - nomenclature: sometimes even an open chain of segments is called a polygon
- definition of inside is intuitive for a simple polygon
- how to check if a point
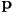 is inside a simple polygon?
is inside a simple polygon? - a polygon is convex if, for any two points
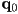 and
and 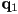 both inside the polygon, all points along the segment from
both inside the polygon, all points along the segment from 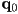 to
to 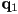 are also inside the polygon
are also inside the polygon - have already covered point-in-polygon test for convex simple polygons: e.g. consider the edges in counter-clockwise order (this is conventional) and then check if
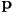 is on or to the left of every edge
is on or to the left of every edge - for non-convex polygons, one solution is to tessellate: break the polygon into a set of convex pieces, and then check each piece separately (will cover this later)
- it is also possible (and classical) to perform insideness checks without tessellating
- two common conventions: “even-odd” rule, and “nonzero” (aka “winding”) rule
- in each case, construct a ray
 in an arbitrary direction from the test point
in an arbitrary direction from the test point 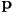
- even-odd rule
- count number of intersections of
 with the polygon.
with the polygon. 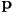 is defined to be inside the poly if the intersection count is odd.
is defined to be inside the poly if the intersection count is odd. - reasoning: each time an edge is crossed, either switch from inside to outside or outside to inside
- but since poly is closed, know that ray must end up outside
- nonzero rule
- again compute all intersections of
 with the poly edges
with the poly edges 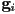 , but this time keep track of whether the edge
, but this time keep track of whether the edge 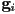 crossed
crossed  from left to right (i.e.
from left to right (i.e. 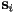 on left side of
on left side of  and
and 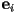 on right side of
on right side of  ) or right to left
) or right to left - count +1 for left-to-right and –1 for right-to-left
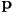 is defined to be inside the poly if and only if (iff) final count is nonzero
is defined to be inside the poly if and only if (iff) final count is nonzero- reasoning: consider sweeping a point
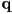 along the perimeter of the poly
along the perimeter of the poly - take the integral of the orientation angle of the line segment from
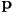 to
to 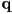
- turns out that, for one complete sweep of the polygon, the integrated winding angle will be an integer multiple
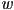 of
of 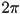
- intuition: reasonable definition of inside-ness is to check if the poly “circled around”
 in CCW direction different number times than in CW direction
in CCW direction different number times than in CW direction - nonzero intersection test turns out to be a shortcut to compute
 (proof is a little subtle and we will not cover it)
(proof is a little subtle and we will not cover it)
- these two rules can produce different results!
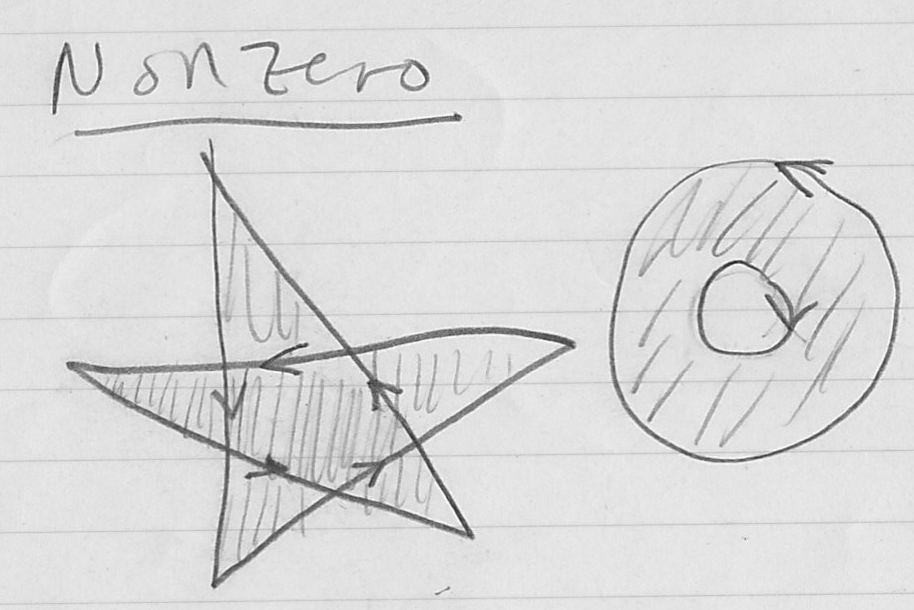
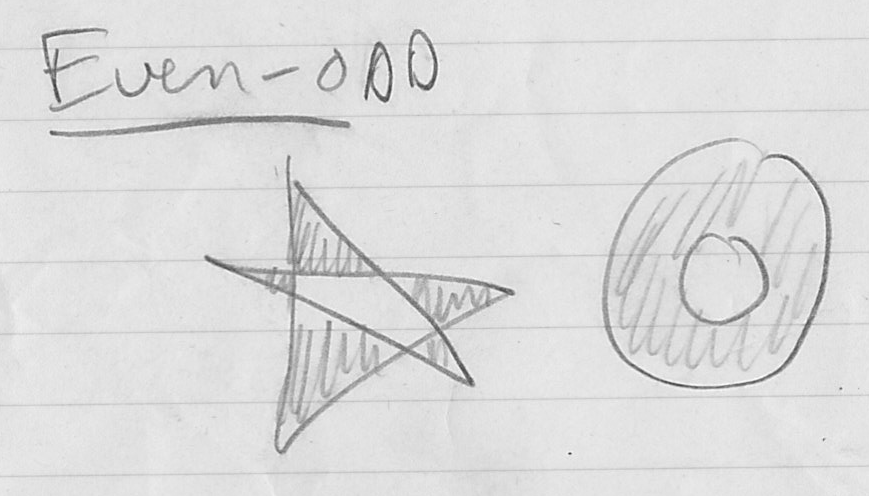
- note that nonzero rule requires external boundary of poly to be in opposite winding order than holes (e.g. CCW for outside, CW for holes)
- no clear “winner”, simply a matter of choice
- some APIs only implement one rule or the other
- Both rules can run into problems if
 intersects polygon right on a vertex. In that case, just start over with a different
intersects polygon right on a vertex. In that case, just start over with a different  . A random choice of
. A random choice of  (remember, any ray will do) will not touch any vertex “with probability 1” (in continuous coords; “with high probability” in discrete coords, like floating point or integer).
(remember, any ray will do) will not touch any vertex “with probability 1” (in continuous coords; “with high probability” in discrete coords, like floating point or integer).
- to rasterize a convex simple polygon, one general approach is
- for
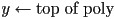 to
to 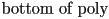
- the details of figuring out the top, bottom, and horizontal extent of the poly at each line can be worked out, even in extensions to non-convex and non-simple polys (using either even-odd or nonzero fill rule)
- we will not cover the details, because in practice, it is becoming less common to rasterize polygons in this way
- instead, most systems are now simply tessellating the polygon into triangles (even if convex) and then rasterizing the triangles
- we will cover tessellation into triangles later today, and rasterizing triangles next time
- what about non-simple polygons?
- the edges may self-intersect
- there may be holes
- there may be degenerate components
- these complicate both point-in-polygon testing and rasterization algorithms
- in practice, self-intersecting polys don’t seem to have many important uses
- but still generally good to be able to handle them, because e.g. a poly may accidentally become self-intersecting due e.g. to numerical imprecision
- or user may simply draw a self-intersecting poly
- holes are sometimes useful: consider drawing a picture of a donut!
- how to even define “inside-ness” for a non-simple polygon?
- even-odd and nonzero rules still can be applied, and in this case can be considered definitional
Tesselation
- in general, tessellation is the process of dividing an arbitrary polygon into a disjoint union of smaller polys
- most common case in practice is to tessellate into triangles because
- triangles are the simplest non-degenerate polygon
- triangles are always convex
- tessellation into triangles is specifically called triangulation
- fact: any simple polygon with
 sides can always be tessellated into exactly
sides can always be tessellated into exactly 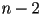 triangles
triangles - this is minimal, though it is also possible to use more triangles
- easy to see for convex simply polys
- pick any arbitrary vertex
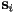
- draw diagonals from
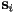 to all other vertices
to all other vertices - done!
- number of diagonals will always be
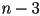
- there will be one triangle per diagonal, plus “the last one”
- the resulting array of triangles can be efficiently stored as a triangle fan, which we will discuss in more detail next time
- in fact, even non-convex simple polys can be tessellated into
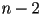 triangles, but a more involved algorithm is required
triangles, but a more involved algorithm is required - extensions also exist for non-simple polys, but we will not cover them
- what is the computational complexity of triangluating a simple polygon?
- note that a lower bound is
 , because at least
, because at least 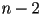 triangles must be produced
triangles must be produced - in 1991, Chazelle demonstrated an
 algorithm, but it’s complex and not typically implemented
algorithm, but it’s complex and not typically implemented - reasonably simple
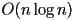 algorithms exist, and are used in practice
algorithms exist, and are used in practice - a randomized alg that is probabilistically
 is also often used
is also often used
- we will study a particularly simple algorithm called ear clipping that is
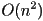
- hence, not optimal, but can still be reasonably fast in practice for polys with relatively few vertices
- We have already defined “convexity” in terms of a whole polygon. We can also say that an individual vertex is convex if the internal angle at that vertex is less than
 radians; otherwise it’s convcave or reflex.
radians; otherwise it’s convcave or reflex. - an ear is a sequence of three consecutive vertices
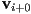 ,
, 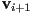 ,
, 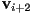 where
where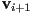 is convex and
is convex and- the triangle formed by the three vertices includes no other vertex
- terminology: the segment from
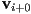 to
to 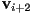 is a diagonal of the polygon, and the vertex
is a diagonal of the polygon, and the vertex 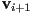 is the ear tip
is the ear tip - fact: a poly with
 always has at least two ears
always has at least two ears - basic idea:
- while
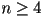
- find an ear and cut it off!
- naive implementation is
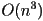
 : until remaining polygon is a triangle
: until remaining polygon is a triangle : check each sequence of three consecutive vertices
: check each sequence of three consecutive vertices : check if every other vertex is outside the candidate ear
: check if every other vertex is outside the candidate ear
- note that the resulting triangulation will have exactly
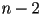 triangles, because each time an ear is cut off one triangle is produced and one vertex is consumed
triangles, because each time an ear is cut off one triangle is produced and one vertex is consumed - a faster
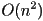 implementation is also relatively simple
implementation is also relatively simple : label all original vertices as either convex or reflex
: label all original vertices as either convex or reflex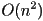 : find all ear tips of the original poly by checking for each convex vertex whether any reflex vertex is inside the corresponding candidate ear
: find all ear tips of the original poly by checking for each convex vertex whether any reflex vertex is inside the corresponding candidate ear : repeat until
: repeat until 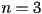
 using e.g. linked list datastructures: cut off the first currently known ear
using e.g. linked list datastructures: cut off the first currently known ear 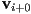 ,
, 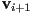 ,
, 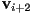
- “repair” the datastructures for the adjacent vertices
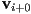 and
and 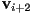
- if vertex was convex, then it is still convex
- if vertex was reflex, it may become convex
 : each adjacent vertex that ends up convex needs to be (re-)tested for “ear-tip-ness”, again by checking if any reflex vertex is inside the ear
: each adjacent vertex that ends up convex needs to be (re-)tested for “ear-tip-ness”, again by checking if any reflex vertex is inside the ear
- example
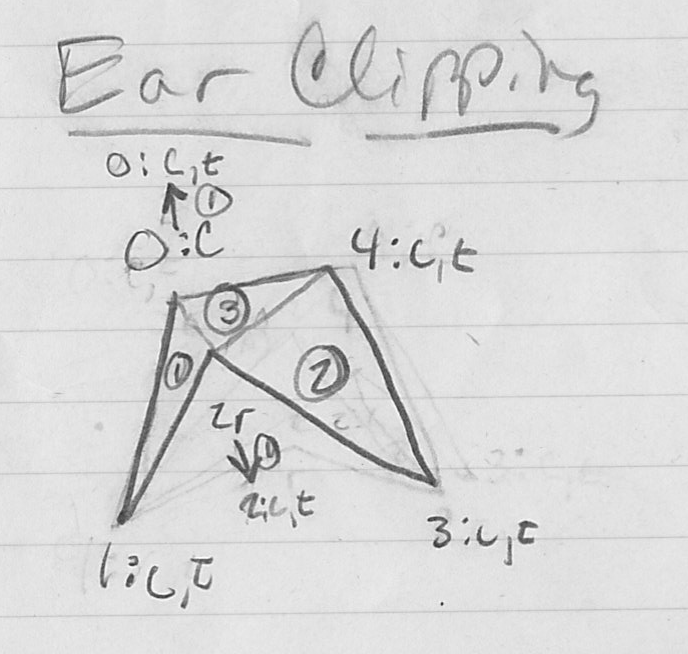
- writing a fast, small, portable, and general triangulation library is apparently a tall order
- almost like writing a good image compression/decompression library
- in practice, a number of algorithms exist, with licenses ranging from public domain to proprietary
- see e.g. here for an account many commonly available libraries and their advantages and disadvantages
Next Time
- reading on website
- triangle meshes
- barycentric coordinates
- rasterizing triangles
 giving the *upper left corner (i.e. the corner with minimum
giving the *upper left corner (i.e. the corner with minimum 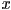 and
and  coordinates) plus (non-negative) width
coordinates) plus (non-negative) width 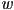 and height
and height 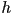 (horizontal and vertical extents, respectively)
(horizontal and vertical extents, respectively)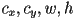 are all integers (pixel coords) but some APIs allow floating point rects as well
are all integers (pixel coords) but some APIs allow floating point rects as well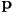 is in a rect:
is in a rect:  and
and 
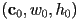 and
and 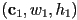 overlap iff
overlap iff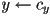 to
to 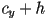
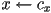 to
to