Computer Graphics (CS 4300) 2010S: Lecture 14
Today
- keyframe animation
- pose interpolation in 2D
- navigating in 2D
Keyframe Animation
- till now we have mainly studied how to create static scenes, i.e. with objects that don’t move
- one exception is that we know how to apply affine transformations to set the pose (position and orientation) of an object defined in a local coordinate frame with respect to an enclosing global frame
- most of you now have experience implementing moving objects by simply changing this transformation and then re-drawing the scene
- if the change you make between each redraw is small enough, the object will appear to move continuously
- one way to achieve this is to make changes in response to mouse motion events, which are typically reported frequently enough that the relative motion from the last event is only a few pixels
- in fact, this is how virtually all “moving pictures” work, whether they were recorded from live motion, generated by a computer, or drawn by hand: by quickly presenting a series of static images, each with an object in a slightly different pose, the human eye and brain “sees” an object which appears to actually be moving
- as you probably know, television and film both work this way, and present a new image at a rate of about 30 times per second (30 frames per second or FPS)
- each individual frame is of course a static image; if no further frames were to be shown, then the motion would appear to “freeze”
- ~30 FPS (actual systems use slightly different rates in practice for various implementation reasons) is chosen because this rate has been empirically found to be a good trade-off between visual quality and complexity of the system
- the faster an object is moving, the more different subsequent frames will be
- so for a fixed framerate, as an object moves faster, its motion will be represented with fewer samples, and this eventually starts to look bad
- this is yet another instance of taking discrete samples of a continuous physical process
- but faster framerates are harder to implement, because more data needs to be captured, transmitted, and redisplayed
- for normal “live action” TV and film, the frames are recorded by a camera which simply takes a series of pictures of the real world at the same rate at which they will be played back
- typically, we reserve the word animation to refer to motion sequences that were not captured as images of the real world, but instead were either drawn by hand or by computer
- in either case, it is possible for a human to specify each individual frame exactly
- but this is a lot of work!
- 2H feature film:
frames - it can take roughly from 1 to 10 man-hours to draw a single frame
- there are only about 2000 hours in a typical work year
- so it could take anywhere from about 100 to 1000 man-years of work to draw all frames for a single feature length film!
- to save work, a common technique is to only specify certain important, or key frames in detail
- a computer, or even an army of faster-working humans, then “fills in” the interframes, essentially by interpolating the adjacent keyframes
Pose Interpolation in 2D
- how to implement an algorithm to interpolate between two keyframes?
- normally, the keyframes are not interpolated as raw images
- rather, the animators decide on a vector
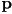of numeric parameters that describe the frame - for example, for a bouncing ball, these might be just the
and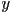 
location of the center of the ball - in general, the pose (placement in space) of any 2D rigid (i.e. non-deformable) object is defined by the location
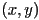of some point on the object and the rotation 
of the object with respect to world frame- i.e., any freely moving object in 2D has three degrees of freedom
- (we didn’t need for the ball example because it’s a special case: the ball is perfectly round)
- interpolating the position 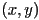of an object, say from
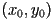to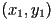
is fairly easy: we just need a curve from 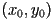to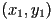 
- as we will see below, for realistic motion, we should ensure that the curve is at least
and 
continuous - note that we can either visualize this as one curve in a 2D space, parameterized by time, or two separate functions
and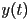 
- what about interpolating the rotation, say from
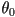to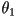 
? - in 2D, it turns out that we can take the same approach as for the position, either considering one curve in a 3D
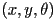space parameterized by time, or three separate curves , , 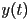and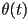 
- later in the course we will see that the situation for 3D objects, which have six degrees of freedom, is not quite as simple
- representing and interpolating orientations in 3D is the main challenge
- but in 2D the orientation is just a scalar , and can be interpolated just like and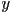
- (in animation, it is also common to include non-positional parameters, such as colors, that might be changing; we will focus on th motion itself)
- any assignment of numbers to 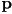should be all the information needed to draw an entire frame
- it is still generally too much work (and too tedious and error-prone) to specify every number for every frame
- so the numbers are only specified at keyframes
- now the interpolation task is reduced to simply interpolating a vector of specific parameters
- how to do that?
- one simple way would be to linearly interpolate from each keyframe to the next
- plotting the value of one parameter vs time, this results in a picewise linear curve
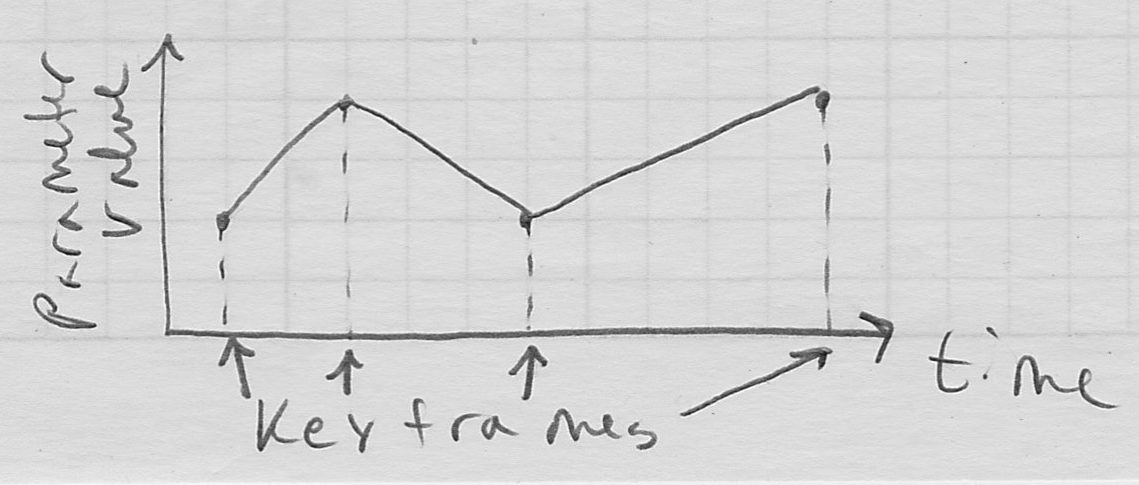
- i.e. the value changes with but not continuity
- for a parameter that represents the position of an object, the slope of the curve corresponds to the object’s velocity (in that dimension)
- fact of physics: real world objects cannot instantaneously change velocity
- thus, the curve for the motion of any real object should always have continuity
- the motion will noticeably look “wrong” otherwise
- fortunately, we already know a few ways to get a spline that interpolates a given set of sample points
- often, a curve is initially generated as a Catmull-Rom spline, because this requires no additional inputs from the user
- the resulting curve can then be tweaked to further optimize the motion in a variety of ways
- one common mathematical approach is called “TCB” (tension, continuity, and bias). It is essentially an extension of the cardinal spline formulation. We won’t study it in detail, but you should know what this acronym refers to and where it is typically used in graphics.
- it is also often necessary to pay attention to the parameterization of the curve, which (as we have studied) effectively controls the speed of the moving object as it follows the prescribed trajectory
- the speed can generally be controlled by re-parameterizing the curve (recall the idea of arc-length parameterization, for example)
Navigating in 2D
- in many applications, it is desirable not only to have individual objects move, but also to allow the entire “world” to be repositioned
- this is called navigation
- for example, in a drawing program, navigation is one way to allow a drawing to be larger than the window in which it is displayed
- think of the drawing as a large sheet of paper
- the window is literally a rectangular opening through which you can see a specific part of that larger paper
- navigation corresponds to moving the paper around
- it is not very hard to implement navigation if you use the right design
- one way to do it is to just insert an additional affine transform
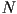that takes coordinates in the world frame (i.e. a frame fixed to or “drawn on” the large sheet of paper) to coordinates in the window 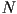- identity corresponds to not having moved the paper under the window
- setting a non-zero translation in 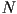corresponds to sliding the paper around, or panning the view
- changing the scale of 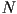corresponds to zooming the view
- typically, 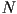never has any rotation, reflection, shear, or non-uniform scale for 2D navigation
- one exception is that, since window coordinates are traditionally “y-down”, if a “y-up” world coordinate system is desired, 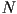can be set up to always implement the necessary reflection
- in 3D, 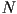works similarly, but typically also includes rotation
- if the transformation taking local coordinates for some specific object to world frame is
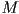, then the transformation going all the way from local to window coordinates is simply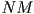 
- i.e. to transform from local to window, first transform from local to world, then world to window
- as a UI consideration, you will need to decide on a way for the user to actually change
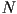
- one possibility is to apply the same mouse or keyboard actions as for moving an object, but make these navigate the entire view whenever no specific object is actually selected
- an approach like this is implemented in the sample code for HW3
Next Time
- review for exam 1
- HW3 due at noon tomorrow!