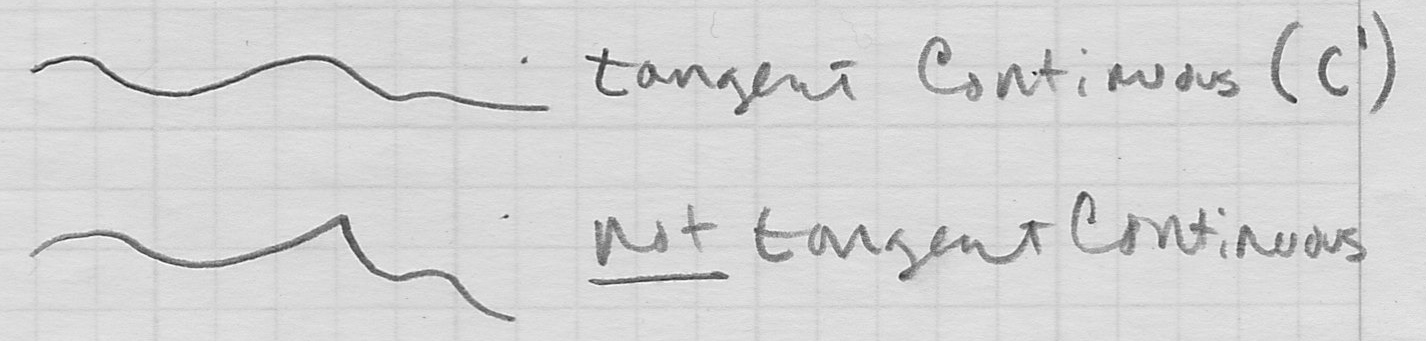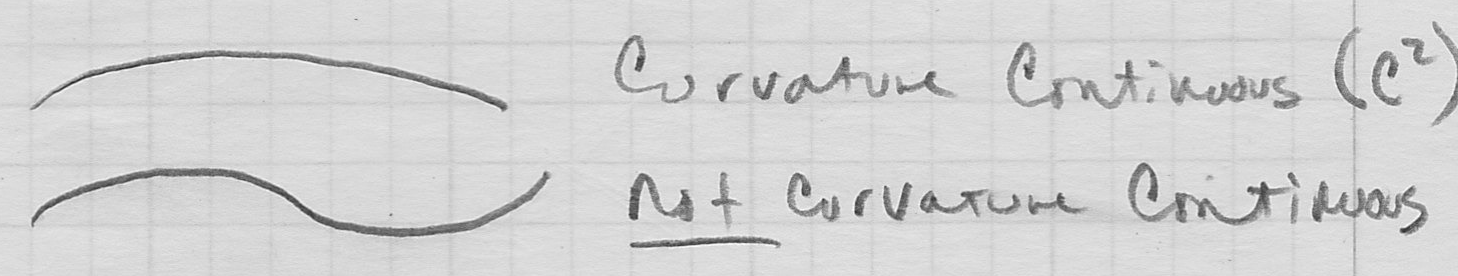Computer Graphics (CS 4300) 2010S: Lecture 11
Today
- finish from last time: scene graphs
- worked example of a coordinate transformation
- introduction to curves in 2D
- parametric curves
- implicit curves
- local curve properties
What is a Curve?
- intuitively, a curve in 2D is “what you get when you draw with a pencil on paper without lifting your hand”
- how can we formalize that intuition?
- observe that curve is effectively a one-dimensional object (i.e., you can know “where you are” along a curve given only one real number), but it is embedded in a two-dimensional space
- this motivates the idea of a continuous mapping from some connected interval
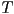 of the one-dimensional real line
of the one-dimensional real line 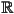 , i.e.
, i.e.  , to the two dimensional space
, to the two dimensional space 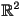
- each 1D point
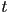 in
in 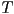 , i.e.
, i.e. 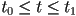 , is mapped to a point
, is mapped to a point  in
in 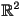
- the collection of all points
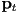 is called the image of
is called the image of 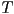 under the mapping
under the mapping - the mapping is continuous iff the image is connected, i.e. if there are no “breaks” in the image
- we will call such an image a curve
- it’s also possible to define a curve to be the mapping itself
- we will allow either or both
 to be infinite, i.e., we will allow curves that “never end”
to be infinite, i.e., we will allow curves that “never end” - also we will allow
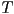 to be either closed (includes both endpoints), open (includes neither endpoint), or half-open (includes exactly one endpoint)
to be either closed (includes both endpoints), open (includes neither endpoint), or half-open (includes exactly one endpoint)
Parametric Curves
- the above development motivates an idea for defining curves given two pieces of information
- a specific parameter interval

- a vector-valued continuous function

- then, for finite
 ,
,- the “first” point on the curve is
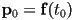
- the “last” point is
 , and
, and - the point
 “moves along” the curve as
“moves along” the curve as 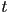 varies from
varies from 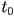 to
to 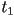
- the continuity of
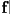 ensures that the image
ensures that the image  , i.e. the set of all points mapped from
, i.e. the set of all points mapped from 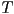 , is continuous
, is continuous
- if
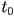 or
or 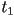 is infinite, or if
is infinite, or if 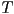 is not closed, the only difference is that there simply is not any “first” or “last” point
is not closed, the only difference is that there simply is not any “first” or “last” point - in general,
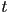 will not be the actual Euclidean distance traveled from
will not be the actual Euclidean distance traveled from 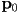 to
to 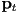 along the curve
along the curve- however, if we happen to know the total length
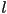 of the curve (i.e. the distance you’d travel if you had to “drive” from
of the curve (i.e. the distance you’d travel if you had to “drive” from 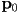 to
to 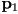 along the curve, not the distance “as the crow flies”), we can re-scale the parametrization and define
along the curve, not the distance “as the crow flies”), we can re-scale the parametrization and define  (assuming
(assuming  ), with
), with  , i.e.
, i.e. 
- this is called an arc length parametrization because
 is the actual distance traveled along the curve from
is the actual distance traveled along the curve from 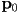 to
to 
- any curve can be arc length parametrized, but to do so essentially requires that the length of the curve be calculated
- because we have given so little restriction on the function
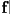 , in general calculating the length of the curve may require computing an integral, and there may be no “closed form” solution (i.e. you could have to numerically integrate to get an approximate answer for
, in general calculating the length of the curve may require computing an integral, and there may be no “closed form” solution (i.e. you could have to numerically integrate to get an approximate answer for 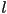 )
)
- example: line segment
- we have already studied the parametric form for a line segment
- given the start and end of the segment as vectors
 ,
, 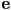
- we take
 and
and 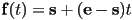
- if we define
 then we can simplify to
then we can simplify to 
- if we want an arc length parametrization, we can use
 with
with 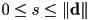
- example: line
- a line is different from a line segment: a segment has finite extent, but a line goes on to infinity in both directions
- implication: in all cases the parameter interval will be unbounded, i.e.

- recall that a line may be given in different forms
- two points
 on the line
on the line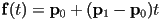 is a parametrization of the line
is a parametrization of the line
- one point
 on the line and a vector
on the line and a vector 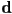 pointing along the line
pointing along the line is a parametrization of the line
is a parametrization of the line
- one point
 on the line and a unit vector
on the line and a unit vector  pointing along the line
pointing along the line is an arc-length parametrization of the line
is an arc-length parametrization of the line
- the unit normal
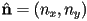 of the line and a distance
of the line and a distance 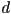 from the origin to the line
from the origin to the line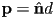 is a point on the line
is a point on the line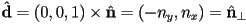 is a unit vector along the line
is a unit vector along the line- proceed as above with
 and
and 
- an orientation
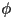 of the unit normal and a distance
of the unit normal and a distance 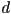 from the origin to the line
from the origin to the line- same as above, with

- an equation of the form
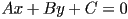
- we’ll discuss this later!
- example: ray
- a ray is a mix between a segment and a line: it’s only infinite in one direction
- assume we’re given the start point
 of the ray and a unit direction vector
of the ray and a unit direction vector 
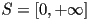 and
and  is an arc-length parametrization of the ray
is an arc-length parametrization of the ray
- example: circle
- given center
 and radius
and radius 
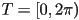 and
and 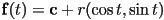
- if we want an arc-length parametrization,
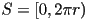 ,
, 
- example: ellipse
- given center
 , horizontal radius
, horizontal radius 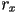 , and vertical radius
, and vertical radius 
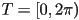 and
and 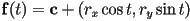
- this produces an axis-aligned ellipse
- for a rotated ellipse, one method is to apply a rotation matrix to

Implicit Curves
- when we studied lines, we learned that an alternative way to describe a line is to give an equation of the form
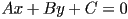
- this is called an implicit equation for the line, because unlike the above parametric forms, it does not give a direct procedure for computing a point on the line given some parameter
- but it does imply all points on the line: a point
 is on the line exactly when the equation holds, i.e. when the expression
is on the line exactly when the equation holds, i.e. when the expression 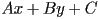 evaluates to zero
evaluates to zero - one reason parametric forms are useful is that the value of the form for an arbitrary point can usually be taken as a measure of the distance from that point to the curve
- there are also implicit forms for some other common curves
- unlike the parametric approach, it is not directly possible to represent a curve with finite endpoints in implicit form
- we will review the implicit form for a line, and then we will give implicit forms for two other common closed curves, i.e., curves without endpoints: circles and ellipses
- example: line
- we have already covered this in detail
- one nice way is to consider we are given a unit normal
 and distance
and distance 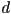 from the origin to the line (i.e. in the direction
from the origin to the line (i.e. in the direction  )
) - any point
 in the plane on the line can be decomposed into a component
in the plane on the line can be decomposed into a component 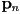 in the direction
in the direction  and a remaining component
and a remaining component 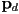 parallel to the line
parallel to the line - i.e.
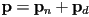
- we can compute
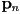 directly as
directly as 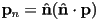
- that is, the scalar
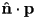 is the length of
is the length of 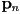 , and
, and  is its direction
is its direction - (in this case it is not necessary to actually calculate
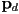 , but if we wanted it, observe that
, but if we wanted it, observe that 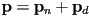 implies
implies 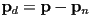 )
) - intuition: the length of
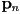 will equal
will equal 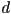 iff
iff  is on the line
is on the line - thus a valid implicit equation for the line is
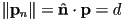 or, rearranging,
or, rearranging, 
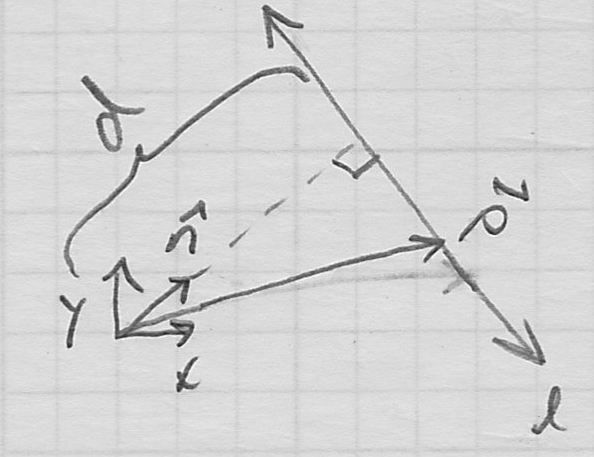
- this is just a fancy way to write
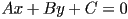 , i.e.
, i.e.  ,
, 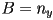 ,
, 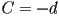 .
. - as we have seen before, a similar equation works even given a normal vector that may not be unit length, and any set of constants
 can be interpreted as giving a normal vector
can be interpreted as giving a normal vector 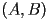 and scaled distance
and scaled distance  , as long as
, as long as 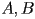 are not both zero
are not both zero - but given a unit normal, the value of the expression
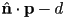 is the actual Euclidean distance from
is the actual Euclidean distance from  to the line (otherwise, it will be a scaled distance)
to the line (otherwise, it will be a scaled distance) - in any case, the sign of
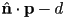 tells us what side of the line
tells us what side of the line  is on:
is on:- if positive,
 is on the “left” of the line, where that is defined to be the side that the normal vector “points towards”
is on the “left” of the line, where that is defined to be the side that the normal vector “points towards” - if negative,
 is to the “right” of the line
is to the “right” of the line - and of course
 is on the line exactly when
is on the line exactly when 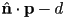 is zero
is zero
- example: circle
- intuition: the Euclidean distance from a point on the circle to the center of the circle must equal the circle radius
- so given the circle center
 and radius
and radius  , a point
, a point  is on the circle exactly when
is on the circle exactly when 
- rearranging gives
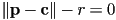
- the expression
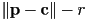 will be negative for all points strictly inside the circle, and positive for all points strictly outside
will be negative for all points strictly inside the circle, and positive for all points strictly outside - in fact, it is easy to see that
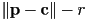 is the Euclidean distance from
is the Euclidean distance from  to the nearest point on the circle
to the nearest point on the circle
- example: ellipse
- given center
 , horizontal radius
, horizontal radius 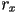 , and vertical radius
, and vertical radius  , apply a scale matrix to the equation for a unit-radius circle:
, apply a scale matrix to the equation for a unit-radius circle: 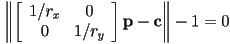
- this is an implicit equation for an axis-aligned ellipse
- this can be rewritten in component form as
 , and if
, and if  , we get an equation that may be familiar to you:
, we get an equation that may be familiar to you: 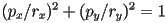
- value will still be negative for
 strictly inside ellipse, positive for
strictly inside ellipse, positive for  strictly outside, but does not give the actual Euclidean distance from
strictly outside, but does not give the actual Euclidean distance from  to the nearest point on the ellipse
to the nearest point on the ellipse
Local Curve Properties
- a local property of a curve is something we can say about the curve at a given point on the curve, only considering the local neighborhood around that point
- for example,
- what direction is the curve “facing”, i.e. what is the tangent to the curve?
- how fast is the curve “bending”, i.e., what is the curvature here?
- are we at an endpoint, i.e. is the curve continuous at this point?
- contrast these with the following global properties:
- does the curve have any endpoints?
- does the curve ever cross itself?
- if the curve is closed, what area does it contain?
- we will now develop methods for finding some local properties of a parametric curve
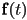
- we can always find a local tangent vector
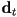 to a parametric curve at a given point
to a parametric curve at a given point  by taking the vector derivative of the curve
by taking the vector derivative of the curve- that is, if
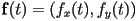 , then
, then 
- the length of this vector
 is the speed of the curve at
is the speed of the curve at 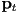 (or just “at
(or just “at 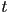 ”), and the direction is the “forward” direction of the curve at that point
”), and the direction is the “forward” direction of the curve at that point - it turns out that if the curve is arc-length parametrized then its speed will always be 1
- for a line given as
 ,
, 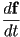 is just
is just 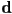
- for an arc-length parametrized line given as
 ,
, 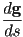 is just
is just  , a unit vector as expected
, a unit vector as expected - for a circle given as
 with
with 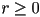 ,
,  , so the speed is always
, so the speed is always  and
and 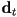 is always tangent to the circle, pointing CCW
is always tangent to the circle, pointing CCW - for an arc-length parametrized circle
 with
with 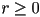 ,
, 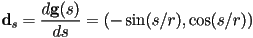 , same as before but now with unit magnitude (since
, same as before but now with unit magnitude (since 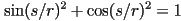 )
) - for an ellipse given as
 with
with  ,
,  , so the speed varies but
, so the speed varies but 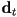 still always tangent to the ellipse and points CCW
still always tangent to the ellipse and points CCW
- we can similarly always find a local normal vector
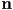 to a parametric curve at a given point
to a parametric curve at a given point  by taking the vector second derivative of the curve
by taking the vector second derivative of the curve- that is, if
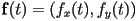 , then
, then 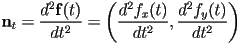
- when the curve is arc-length parametrized,
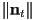 is called the curvature at
is called the curvature at 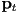 (or just at
(or just at 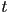 )
) - for an arc-length parametrized line given as
 ,
,  is
is 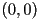 , i.e. the line has no curvature
, i.e. the line has no curvature - for an arc-length parametrized circle
 with
with 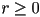 ,
, 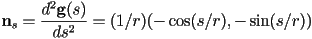 , so the curvature is always
, so the curvature is always 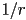 , and
, and 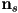 always points inwards
always points inwards - we haven’t presented an arc-length parametrized ellipse, but for an ellipse given as
 with
with  ,
,  , so
, so 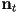 still at least always points inwards
still at least always points inwards
- a parametric curve has local position continuity (or simply “is continuous”) at
 iff the limit of
iff the limit of 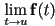 is the same approaching from either direction
is the same approaching from either direction- this is just a precise way to say that the curve can be “drawn without lifting your pencil”

- this is also referred to as
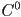 continuity, for reasons we will see shortly
continuity, for reasons we will see shortly - actually, by the way we defined a “curve”, every curve has
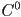 continuity
continuity - but sometimes, in particular when we talk about assembling a piecewise curve from individual parts, we need to be aware of
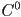 continuity
continuity
- similarly, a parametric curve has local tangent continuity at
 iff the limit of the first derivative
iff the limit of the first derivative 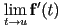 is the same approaching from either direction
is the same approaching from either direction- intuitively, this means the curve does not have a sharp “kink” at

- this is also called
 continuity
continuity - again, this is particularly useful when dealing with the joining of piecewise curves
- note that if the curve is not arc-length parametrized then it’s possible for the tangent vectors approaching from either direction to have the same (or opposing) direction but different magnitudes
- technically our definition, which is based on parametric continuity, would say that the curve is not
 continuous in this case
continuous in this case - if we don’t want to care about this, we can take a slightly modified definition of geometric continuity where we only care that the tangent vectors have the same direction
- finally, a parametric curve has local curvature continuity at
 iff the limit of the second derivative
iff the limit of the second derivative 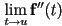 is the same approaching from either direction
is the same approaching from either direction- intuitively, this means that the curve “bends in a consistent direction” at

- this is also called
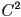 continuity (see the pattern?)
continuity (see the pattern?)
 continuity is similarly defined for any integer
continuity is similarly defined for any integer 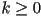
- a curve is smooth if it is
 continuous for all
continuous for all 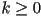
- though sometimes people use the word smooth to mean just that there is some
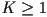 such that the curve is
such that the curve is  continuous for all
continuous for all 
- we can also write in that case that the curve is “
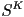 smooth”
smooth”
Next Time
- reading on website
- polynomial curves in 2D
- interpolating polynomials in 2D
- interpolating splines in 2D
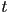 in
in 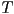 , i.e.
, i.e. 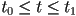 , is mapped to a point
, is mapped to a point  in
in 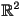
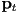 is called the image of
is called the image of 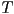 under the mapping
under the mapping