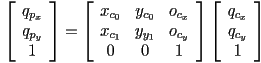Computer Graphics (CS 4300) 2010S: Lecture 10
Today
- rigid transformations in 2D
- non-rigid transformations in 2D
- homogeneous coordinates
- scene graphs
- barycentric coordinates are one example of a child frame defined with respect to a parent frame
- we will now take a step back and study this in more generality
- we will separate our study into two cases
- first we will look at rigid transforms, where the child frame has an orthonormal basis
- then we will relax that constraint and consider non-rigid transforms
- a coordinate transform, or just a transform, is a formula that takes the coordinates
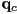 of a point in the child frame and returns the parent-frame coordinates
of a point in the child frame and returns the parent-frame coordinates 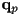 of the point
of the point - we have already seen that, if we know the origin
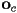 and basis
and basis 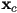 ,
, 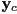 of a child frame (these are all vectors in parent frame), then the coordinate transform from child to parent frame is just
of a child frame (these are all vectors in parent frame), then the coordinate transform from child to parent frame is just 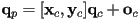
- i.e. if
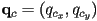 then
then 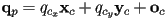
- technically, this is called an affine transform
- this is highly useful in graphics because we frequently would like to describe an object with respect to “its own” coordinate frame, and then “place” that object somewhere in a parent frame
- in this case, all we have to do is
- compute
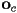 as the vector from the parent frame origin to the origin of the placed child frame
as the vector from the parent frame origin to the origin of the placed child frame - find the parent-frame coordinates of the vectors
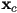 and
and 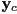 according to the placement of the child frame (e.g. they will depend on the rotation of the child frame with respect to the parent, if any)
according to the placement of the child frame (e.g. they will depend on the rotation of the child frame with respect to the parent, if any)
- then the above coordinate transform formula can be applied to the child frame coordinates of every point of the object, and the result will be the corresponding parent frame coordinates of the placed object
- example of “house” with
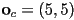 ,
, 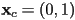 ,
, 
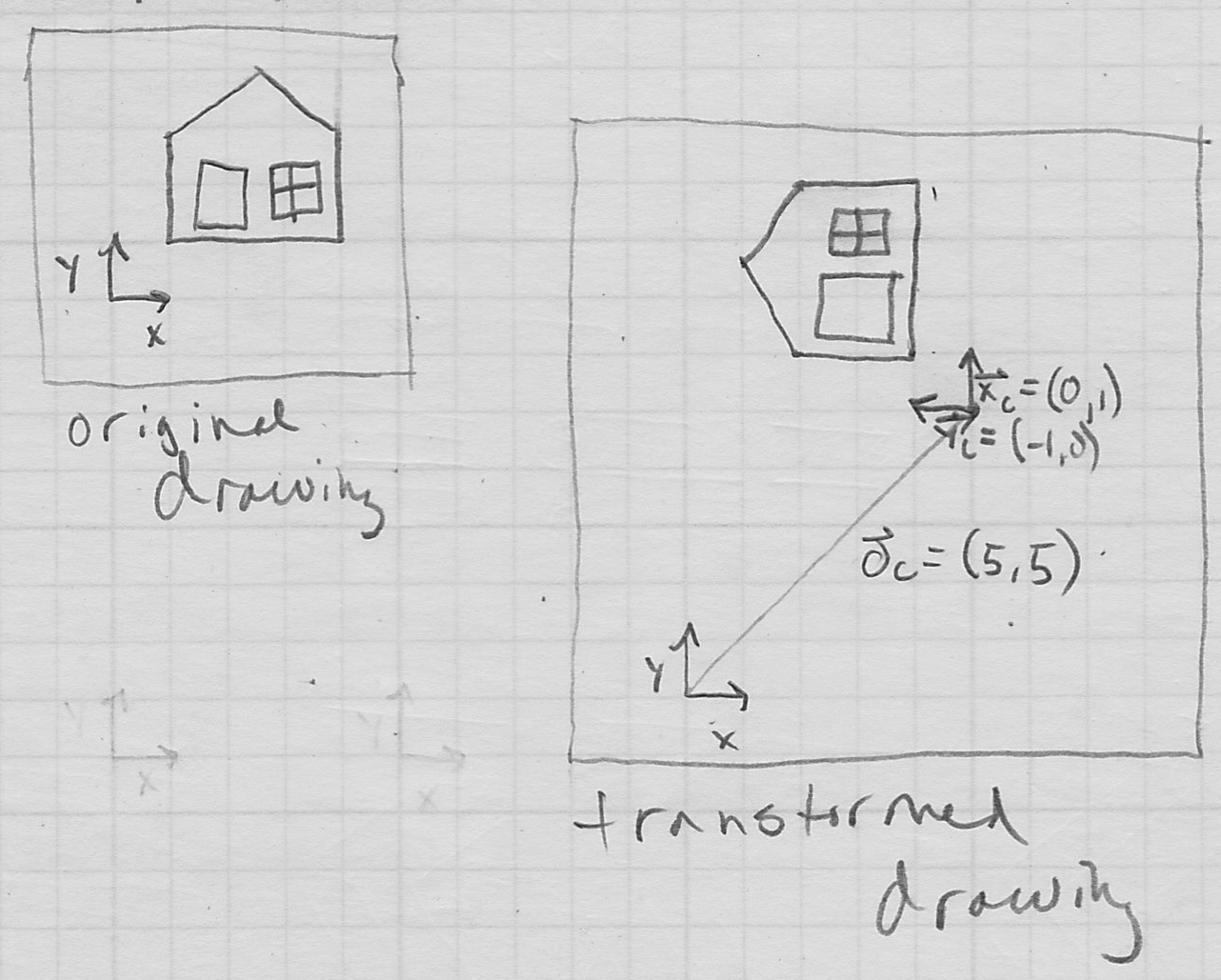
- when
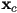 ,
, 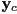 are orthonormal this is called a rigid transformation because it can be shown that in this case the (Euclidean) distance between any pair of points on the object in child frame will be preserved by the transformation; i.e. the corresponding parent frame points will be separated by the same distance
are orthonormal this is called a rigid transformation because it can be shown that in this case the (Euclidean) distance between any pair of points on the object in child frame will be preserved by the transformation; i.e. the corresponding parent frame points will be separated by the same distance - for this reason, rigid transformations are also called Euclidean transformations
- all rigid transformations can be broken down into three basic operations: translation, rotation, and reflection
- i.e. any given rigid transform is some combinination of translation, rotation, and reflection
- we will study combining or composing transforms later
- translating
- the case where
 and
and 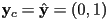 always results in a translation
always results in a translation - the orientation of the object is not changed
- but the object can be “slid around” in parent frame by different settings of
- rotating
- the case where
 and
and 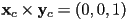 (recall that to take the cross product of two 2D vectors, extend each to 3D with
(recall that to take the cross product of two 2D vectors, extend each to 3D with 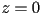 ) constitutes the space of all pure rotation transforms
) constitutes the space of all pure rotation transforms - here, the origin of the child frame always remains at the origin of the parent frame
- but the object can now rotate arbitrarily
- given a desired rotation
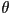 of the object in CCW radians, how to compute
of the object in CCW radians, how to compute 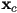 and
and 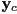 ?
?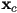 is the rotation of
is the rotation of 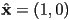 by
by 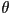
- basic trig:
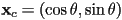
- now construct
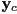 perpendicular to
perpendicular to 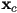 s.t.
s.t. 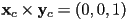 (extending 2D vectors to 3D with
(extending 2D vectors to 3D with 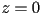 )
) - as we learned before, one way to do this is to calculate
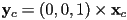
- so
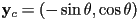
- reflecting
- note that no matter what amount of translation and rotation you do, you will never be able to “mirror” the object, i.e., reflect it across some line
- it turns out to be sufficient to enable reflection across the
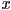 and
and 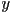 parent-frame axes
parent-frame axes- reflection about an arbitrary line can then be accomplished by composing this with rotation and translation
- in these cases
 , i.e. the origin of the child frame again always remains at the origin of the parent frame
, i.e. the origin of the child frame again always remains at the origin of the parent frame - to mirror about the
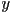 axis,
axis, 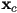 must go from
must go from 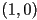 to
to  , but
, but 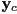 must remain unchanged at
must remain unchanged at 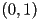
 and
and 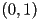 are orthonormal, so we are done:
are orthonormal, so we are done:  and
and 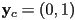
- what about the fact that
 ?
?- we might care about this because (as we just saw) even when working in 2D it is sometimes useful to consider the
 axis
axis - we can either consider the mirrored frame to be a right-handed 3D frame with its
 axis pointing into the screen, or as a left-handed 3D frame with its
axis pointing into the screen, or as a left-handed 3D frame with its  axis pointing out of the screen
axis pointing out of the screen
- similar reasoning to mirror about
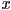 -axis:
-axis:  and
and 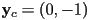
- mirroring about both the
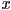 and
and 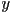 axes is not a reflection; it’s a rotation by
axes is not a reflection; it’s a rotation by 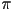 radians
radians
- note that in a “planar world”, there is no way to move a rigid physical object so that it becomes its mirror image
- in fact, the only possible transformations of a rigid object that must “live on the plane” are rotations and translations
- these are called displacements; they model the possible motions of actual (physical) rigid objects
- same will hold in 3D: the only displacments are rotations and translations
- we now cover the non-rigid but invertible transforms
- this means we are going to relax the constraint that
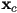 and
and 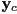 are orthonormal
are orthonormal - but we are going to insist that
- both basis vectors always have non-zero length, i.e.
 and
and 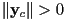
- the basis vectors are never parallel or anti-parallel, i.e.
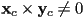
- as we will see later, this will ensure that the resulting transforms are always invertible, i.e., that they can be undone
- the invertible non-rigid transforms break down into two basic operations: scaling and shearing
- in practice, in most areas of graphics,
- rigid transforms are very common (with displacements being the most common)
- scale transforms are somewhat common
- shear transforms are not very common
- non-invertible transforms are uncommon
- scaling
- keeping
 and the basis vectors orthogonal, i.e.
and the basis vectors orthogonal, i.e.  but allowing their lengths to vary results in a scale transform
but allowing their lengths to vary results in a scale transform - let
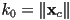 and
and 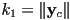
- enforce that
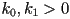 (else we could have a non-invertible transform or a reflection)
(else we could have a non-invertible transform or a reflection) - then
 is the magnification of the local frame with respect to the oworld frame along the local frame’s
is the magnification of the local frame with respect to the oworld frame along the local frame’s 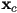 axis, and
axis, and 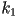 is similarly the magnification along the
is similarly the magnification along the 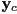 axis
axis - the case
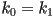 is called uniform scale; else the scaling is non-uniform
is called uniform scale; else the scaling is non-uniform
- shearing
- again, keep
 but now allow the basis vectors to be non-orthogonal
but now allow the basis vectors to be non-orthogonal - the result is a diagonal “squishing” or “stretching” of the local frame with respect to the world frame
- common convention is to either keep
 and set
and set 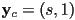 , producing a horizontal shear or to set
, producing a horizontal shear or to set 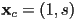 and keep
and keep 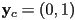 , producing a vertical shear
, producing a vertical shear
Homogeneous Coordinates
- looking again at the basic transformation equation
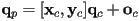 , note that it consists of two operations:
, note that it consists of two operations:- one multiplication of a
 matrix by a
matrix by a  vector
vector - one addition of two
 vectors
vectors
- it turns out that it’s possible to rewrite this as a single matrix-vector multiplication
- this is called homogenization
- first, extend
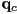 to 3D with
to 3D with 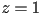
- note that previously we sometimes have extended a 2D vector to 3D with
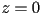 ; this is different
; this is different - we call the representation of an
 -dimensional vector in
-dimensional vector in  dimensions with the last coordinate value 1 homogeneous coordinates
dimensions with the last coordinate value 1 homogeneous coordinates
- second, let
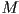 be a
be a  matrix
matrix 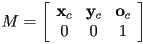
- now
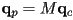 transforms the homogeneous child frame coordinates to the homogeneous parent frame coordinates
transforms the homogeneous child frame coordinates to the homogeneous parent frame coordinates
- expanding this out,
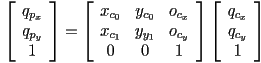
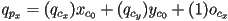
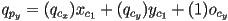
- so, just as before,
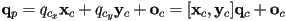
- the third coordinate remains
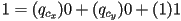
- note that this works for any affine transform, even non-rigid (and actually, even non-invertible)
- homogenization is particularly useful when we want to compose or invert transforms
- composition of two homogeneous transforms
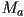 followed
followed  is simply the matrix multiplication
is simply the matrix multiplication 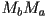
 with
with 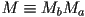
- recall the rules of matrix multiplication:
- associative and distributive but not commutative
- this highlights the fact that the order in which transformations are applied (usually) matters
- the inner matrix dimensions, i.e. the number of columns of the first matrix and the number of rows of the second, must be equal (ok for homogenous transforms, always
 in 2D)
in 2D) - the dimensions of the product are the outer dimensions of the factors, i.e. the number of rows of the first and the number of columns of the second (again, always
 in 2D)
in 2D) - the result is computed by considering the first matrix to be a column vector of row vectors and the second to be a row vector of column vectors, and taking all dot products
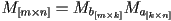

- how many flops?
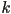 multiplies per element of the result
multiplies per element of the result 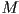
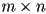 elements
elements- total is
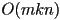
- note if
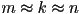 , this is cubic
, this is cubic
- fortunately, homogenous transform matrices are small, and they also have a special form
- let
 be the
be the 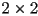 upper-left submatrix of
upper-left submatrix of 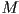 , i.e.
, i.e. 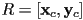
- then
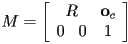 ,
, 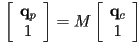 , and
, and 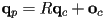
- so for a composition of transforms
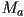 followed by
followed by 
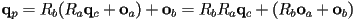
- and if
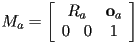 and
and 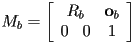
- then we can write
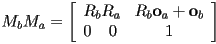
- this saves some FLOPS by using the fact that the bottom row is known
- total
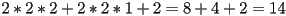 FLOPS vs
FLOPS vs 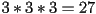 for naieve impl
for naieve impl
- inversion of a homogeneous transform
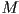 , i.e. finding the corresponding
, i.e. finding the corresponding 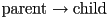 transform, is just the matrix inversion
transform, is just the matrix inversion 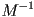
- so if
 then
then 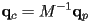
- recall that only square matrices with non-zero determinant are invertible
- there are algorithms to compute the inverse of any given matrix satisfying those constraints
- recalling that
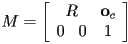 ,
, 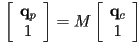 , and
, and 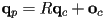
- then solve the last equation for
 in terms of
in terms of 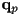 :
: 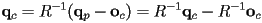
- and we can write
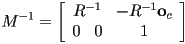
- so we just have to remember how to invert a
 matrix
matrix- if
 then
then 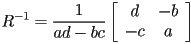
- note that if
 then we would have a divide by zero
then we would have a divide by zero - in fact,
 is the determinant—the matrix is not invertible if this quantity is zero
is the determinant—the matrix is not invertible if this quantity is zero - geometric interpretation: if
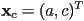 and
and  , then
, then  is the
is the  -component of the cross product
-component of the cross product  , extending both to 3D with
, extending both to 3D with 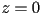
- in this situation,
 is also the magnitude of the cross product
is also the magnitude of the cross product - thus it will be zero if and only if:
- either (or both) of the basis vectors had magnitude zero
- the basis vectors were nonzero-length, but parallel (or anti-parallel)
- for a rigid transform, we know that the basis vectors are orthonormal, so they both have unit length, and they are perpendicular
- thus
 must be either
must be either 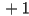 or
or 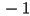 for a rigid transform
for a rigid transform - in fact, it will be
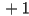 unless
unless  includes a reflection, so when
includes a reflection, so when 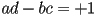
 is called a rotation matrix
is called a rotation matrix - sometimes the upper left submatrix of a homogenous transform is referred to as a “rotation matrix” even when the determinant is not guaranteed to be +1
- when
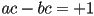 it is not too hard to show that there is always some
it is not too hard to show that there is always some 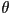 such that
such that 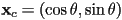 and
and  (this is just a restatement of our derivation of rotation transforms above)
(this is just a restatement of our derivation of rotation transforms above) - i.e.
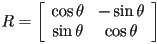
- in this case
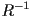 is determined easily by inspection:
is determined easily by inspection: 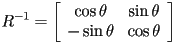
- in general, for any orthogonal matrix,
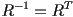 , i.e. the inverse is just the transpose
, i.e. the inverse is just the transpose
- finally, recall that the inverse of a product of matrices is the product of the inverses in reverse order, i.e.
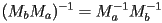
Scene Graphs
- why limit ourselves to a single child frame?
- we can easily have, e.g. one child frame per object in the scene
- the resulting structure is topologically a tree with depth 1
- we can call the (single) parent frame the world frame, and each child frame an individual local or object frame
- but why stop there? many objects are composed of sub-objects…
- so form a deeper tree, called a scene graph
- now the local-to-world transform for a given object
 ,
, 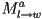 , is the ordered composition of transforms along the tree branch starting at the object and ending at the root of the tree
, is the ordered composition of transforms along the tree branch starting at the object and ending at the root of the tree - and the transform from the coordinate frame of object
 to object
to object 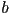 is just
is just 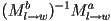
- i.e. transform from
 to world, and then world to
to world, and then world to 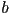
- you can imagine following the transform chain “down” from
 to the root of the tree, and then “up” from there to
to the root of the tree, and then “up” from there to 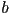
- on the way up, you use the inverse transforms, and you hit them in reverse order
- so this exactly results in the inverse of
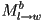
- many operations, such as rendering, require us to traverse the scene graph
- most common method is just a depth-first search starting at the root
- initialize the local to world transform
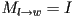
- upon visiting an object
- append the transform
 taking its coordinate frame to that of its parent, i.e.
taking its coordinate frame to that of its parent, i.e. 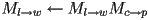
- do whatever needs to be done with the geometry of the object
- e.g., transform to world coordinates and rasterize
- recursively visit all children of the object
- when finished, append
 , or just restore
, or just restore  to the value it had just before visiting the object
to the value it had just before visiting the object
Next Time
- reading on website
- implicit and parameteric curves in 2D
- local curve properties
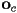 as the vector from the parent frame origin to the origin of the placed child frame
as the vector from the parent frame origin to the origin of the placed child frame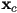 and
and 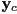 according to the placement of the child frame (e.g. they will depend on the rotation of the child frame with respect to the parent, if any)
according to the placement of the child frame (e.g. they will depend on the rotation of the child frame with respect to the parent, if any)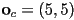 ,
, 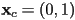 ,
, 

 and
and 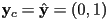 always results in a translation
always results in a translation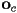
 and
and 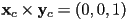 (recall that to take the cross product of two 2D vectors, extend each to 3D with
(recall that to take the cross product of two 2D vectors, extend each to 3D with  ) constitutes the space of all pure rotation transforms
) constitutes the space of all pure rotation transforms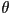 of the object in CCW radians, how to compute
of the object in CCW radians, how to compute 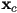 and
and 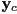 ?
?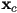 is the rotation of
is the rotation of 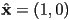 by
by 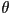
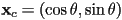
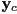 perpendicular to
perpendicular to 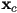 s.t.
s.t. 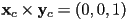 (extending 2D vectors to 3D with
(extending 2D vectors to 3D with 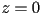 )
)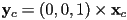
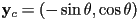
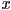 and
and 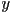 parent-frame axes
parent-frame axes , i.e. the origin of the child frame again always remains at the origin of the parent frame
, i.e. the origin of the child frame again always remains at the origin of the parent frame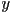 axis,
axis, 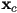 must go from
must go from 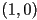 to
to  , but
, but 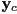 must remain unchanged at
must remain unchanged at 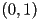
 and
and 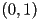 are orthonormal, so we are done:
are orthonormal, so we are done:  and
and 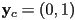
 ?
? axis
axis axis pointing into the screen, or as a left-handed 3D frame with its
axis pointing into the screen, or as a left-handed 3D frame with its  axis pointing out of the screen
axis pointing out of the screen -axis:
-axis:  and
and 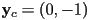
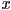 and
and 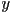 axes is not a reflection; it’s a rotation by
axes is not a reflection; it’s a rotation by 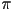 radians
radians