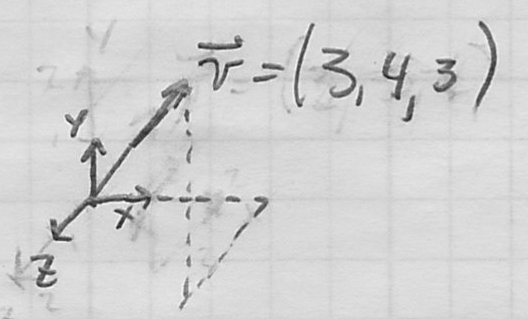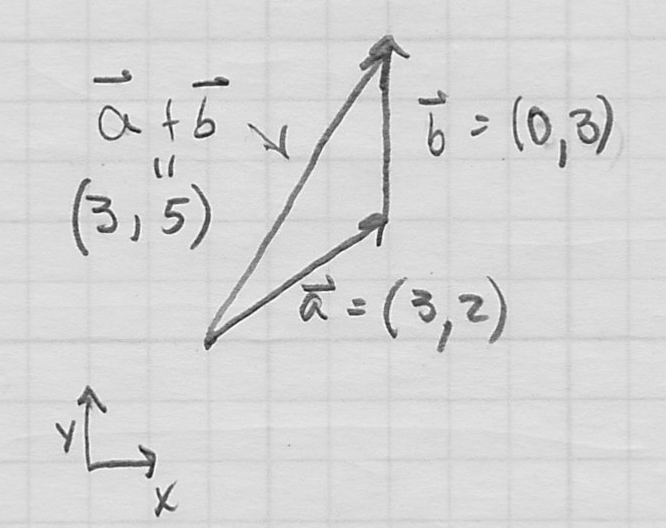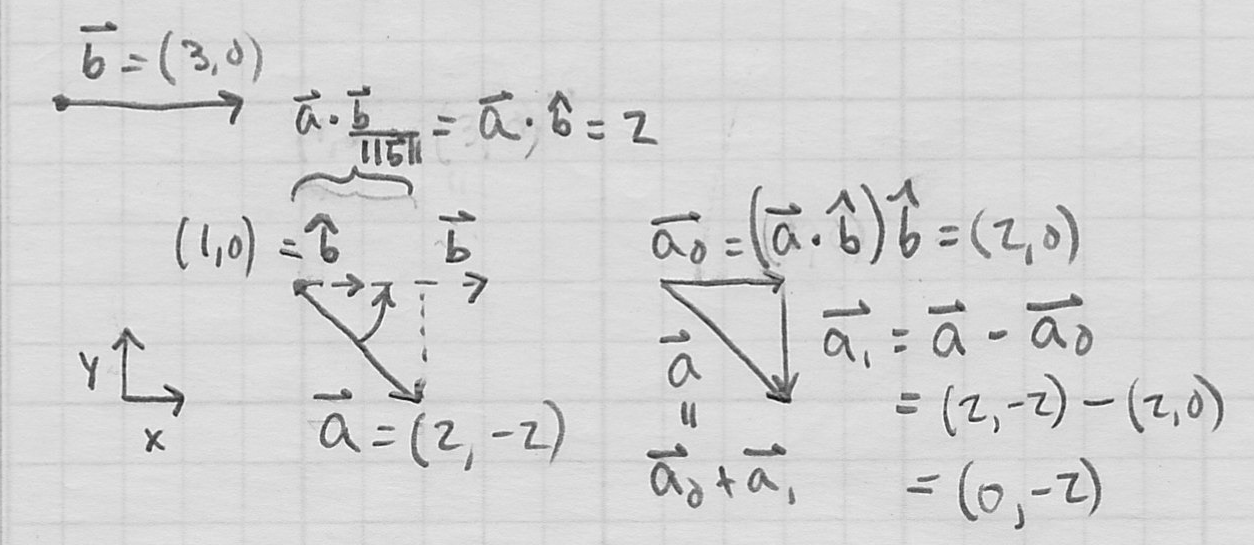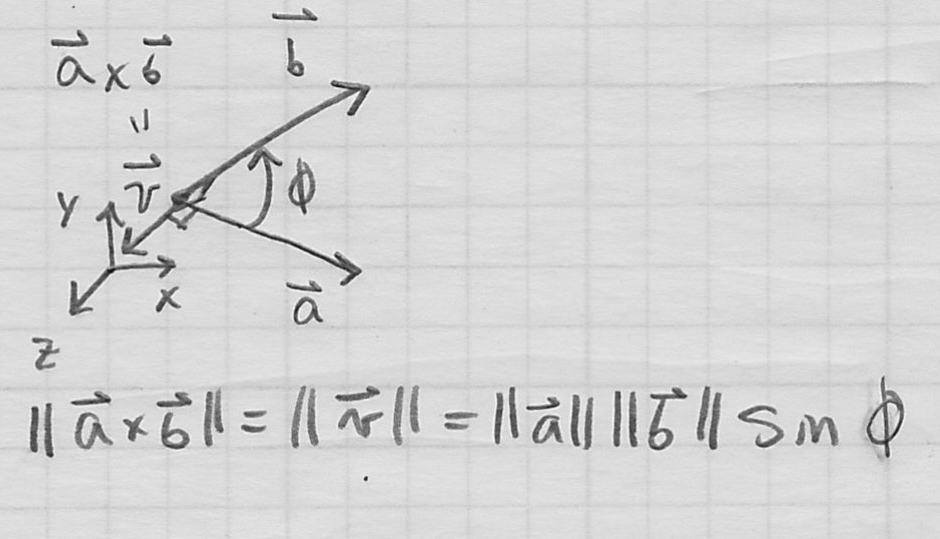Computer Graphics (CS 4300) 2010S: Lecture 1
Today
- HW0 due
- HW1 assigned, due next Weds
- vectors, vector algebra
- floating point algebra
HW1
- 2D “sampler” program
- select a 2D graphics platform
- gain experience working with the primitives on your platform, including both drawing functions and window management
- the next two assignments with be a major 2D project; this first project should help you build a foundation
- or, if you decide you don’t like the platform you use for this project, you can switch
Vectors
- multiple related interpretations for the word “vector”
- in computing, a 1D array
- in math, an element of a linear space
- geometrically, an arrow with magnitude and direction
- text uses this def
- connection with above defs later
- vector names typically lowercase and typeset in bold (e.g.
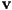 ), or handwritten with over-arrow (e.g.
), or handwritten with over-arrow (e.g.  )
)
- dimension (sometimes size or length, but those terms can be confused with magnitude) of a vector is the number of components
- what are the components of a vector?
- typically scalars
- real numbers
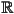
- floating point numbers (more later)
- or possibly complex numbers
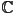 , etc
, etc
- a vector of other vectors (all same dimension) is a matrix (more later)
- matrix names typically uppercase, e.g.
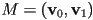
- text sometimes treats a vector of vectors (e.g. representing points) as a vector, e.g.
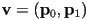
- a vector of scalars can also be considered a matrix
- a “row vector” is an
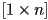 matrix
matrix - a “column vector” is an
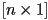 matrix
matrix - matrix dimensions are always written
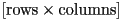
- transpose operation
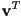 flips row vector into column vector and vice-versa, e.g.
flips row vector into column vector and vice-versa, e.g. 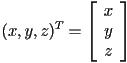
- sometimes a column vector
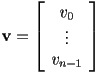 is written as
is written as 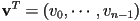 just to be more compact on the page
just to be more compact on the page - transposition is well-defined for all matrices, not just row or column vectors
- sometimes transposition is implied by context (text uses this convention)
- vectors and matrices typically written with either parenthesis or square brackets; often parens only used for row vectors
- in graphics, 2D and 3D vectors of real (typically floating point, in implementations) scalars are very common
- “arrow” def is intuitive in these low dimensions
- connection: components of vector are coordinates of the tip of the vector relative to some reference point in a Cartesian (orthogonal) frame
- always in order
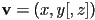
- examples in 2D
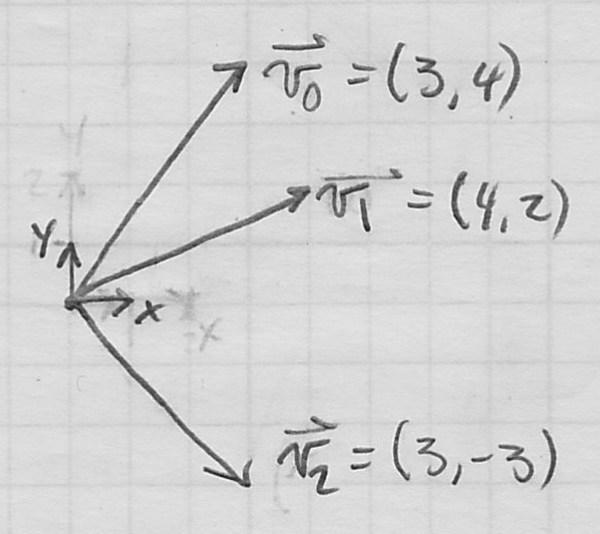
- examples in 3D
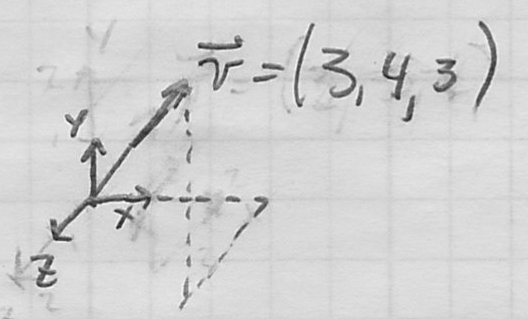
- special notations for vectors perpendicular to plane:

- technically,
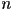 components of
components of 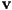 specify a linear combination of
specify a linear combination of 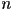 basis vectors (more later)
basis vectors (more later)
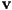 can represent a “location” (“position” or “point”), when reference point is the origin
can represent a “location” (“position” or “point”), when reference point is the origin 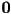
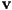 can also represent “offset” or “displacement”
can also represent “offset” or “displacement”- unless otherwise specified, this is the “standard” interpretation of a vector
- in this interpretation, the coordinates of the vector give the location of the end (also called the head or tip) of the vector relative to any arbitrary point serving as the vector start (also called the tail)
- i.e. the vector can be drawn in any location

- as long as length is nonzero,
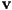 can also just be used to define a direction
can also just be used to define a direction- typically unit vector (length=1) is used in this case
- generalizes to arbitrary dimension, unlike defining direction based on angle
Floating Point Algebra
- an interval of real numbers is the set of all numbers between two limits
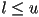
- intervals can be closed (contain the limit, square bracket used) or open (exclude the limit, parenthesis used) on either end
- in any interval
 with
with 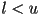 there are is an infinity of other real numbers
there are is an infinity of other real numbers - since the memory of any computer is finite, it is not possible to represent all real numbers on a computer, even within any given bounds
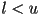
- one solution is to make a finite approximation where a fixed number of bits are used to index a specific finite subset of representable numbers in some large interval
 with
with 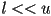
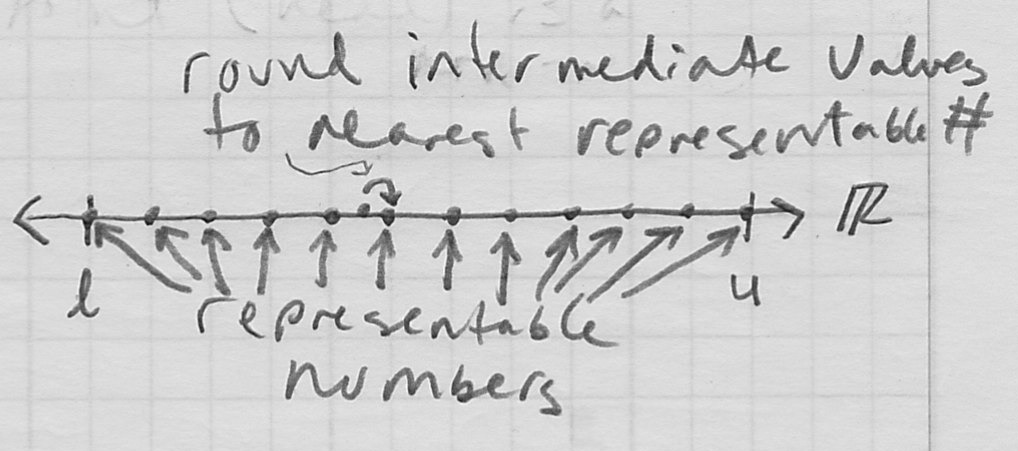
- any other number is typically rounded to nearest representable number
- this includes, in particular, results of mathematical operations on representable numbers
- standard today is IEEE754 floating point
- like scientific notation, but in binary
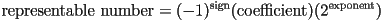
- sign is always represented with one bit
- for 32-bit
float single precision, coefficient is 23 bits and exponent is 8 bits - for 64-bit
double double precision, coefficient is 52 bits and exponent is 11 bits - double is numerically more accurate than single (and has larger range), but takes twice the memory storage, which matters in graphics where models are often based on large arrays of floating point numbers
- single precision is thus common in graphics
- modern CPUs can do both single and double precision floating point math in hardware, at speed roughly equivalent to integer computation
- older graphics algorithms sometimes integer-only for speed, but this is no longer a major concern, except on some smaller embedded platforms
- memory throughput can still make bulk operations faster for single than double
- GPU hardware, except for high-end, is typically limited to single-precision computation (and may even cheat accuracy for speed in some cases!)
- special numbers
- represented by reserved bit patterns
- infinity: what you get when you divide
 with
with 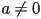
- NaN “not a number”: what you get when e.g. you divide
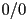
- common mistakes
- 0.1 is not 0.1: when you type a constant in decimal notation, either in sourcecode or as part of the input to your program, be aware that it may not be representable in IEEE754. Typically the nearest representable number will be used instead.
- dividing by very small numbers is usually a bad idea
- proof is a little subtle, but basically reciprocal of a small error is a much larger error
- let
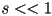 be a small real number,
be a small real number, 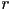 be its representation as a floating point number, and
be its representation as a floating point number, and 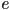 the error:
the error: 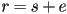
- ask for
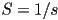 , machine computes
, machine computes 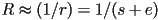
- define error of result
 s.t.
s.t. 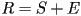
- compare
 to
to 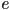 :
: 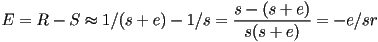
- so
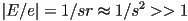
- rule of thumb: whenever you divide, check if the divisor is very small, and if it is, treat as if it were 0
- Often no indication or error when an intermediate result has become infinity or NaN.
- according to some (including text), this is a feature, not a bug
- these values are contagious, e.g.
 ,
, 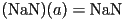
- for further info, see references on course website
Vector Magnitude and Direction
- what is the magnitude of
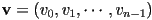 ?
?- take the “2-norm”
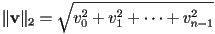
- usually just written
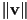
- this is a special case of the Euclidean distance formula between two points, where one point is the origin and the other is the tip of the vector
- normalizing a vector: given
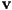 , make a unit vector
, make a unit vector 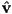
- as long as
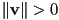 ,
, 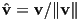
- division of a vector by a scalar will be covered later
- what is the direction of
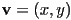 ?
?- as long as
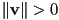 ,
, 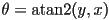
- theta is CCW angle from positive x-axis in radians
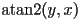 is like
is like 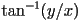 but works in any quadrant, or if
but works in any quadrant, or if 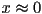 (as long as not
(as long as not  also)
also)- this is in 2D only; idea of vector direction as an angle does not really generalize to higher dimension
- though angle between two vectors is always well defined any dimension
- how to construct a 2D unit vector
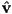 in direction
in direction 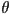 ?
?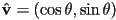
- can also set magnitude
 :
: 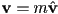
- multiplication of a vector by a scalar will be covered later
- to reverse the direction of a vector, negate it
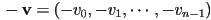
- this works in any dimension
Vector Algebra: Addition and Subtraction
- vector sum:
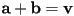
- inputs (addends): two vectors of (same) dimension
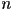
- output (sum): a new vector with dimension
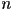
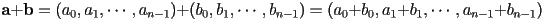
- graphically, place the tail (start) of
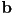 on the head (end or “tip”) of
on the head (end or “tip”) of 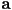
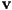 is the vector from the tail of
is the vector from the tail of 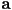 to the tip of
to the tip of 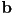
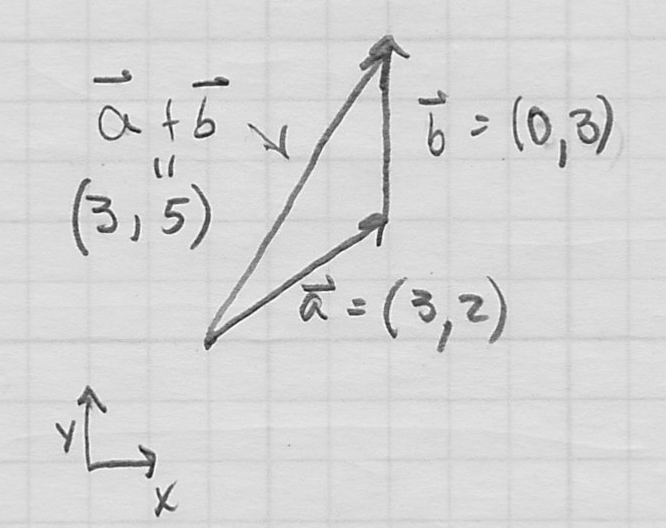
- vector addition is commutative
- graphically, this is the “parallelogram rule”
- typically does not make sense to sum locations (points), but does make sense for offsets (displacements)
- to subtract, first negate the second vector:
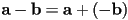
Vector Algebra: Multiplication
- “scalar multiplication”
- multiplying a vector by a scalar
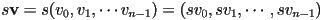
- multiplies the magnitude of
 by
by 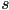 :
: 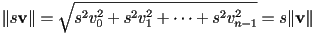
- to divide by a scalar, multiply by the reciprocal
- scalar multiplication is commutative and distributive
- obviously, negation is scalar multiplication by –1
- “scalar” or “dot” product:
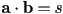
- inputs (factors): two vectors of same dimension composed of scalar components
- output (product): a scalar
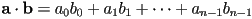
- mainly useful in graphics due to the identity
 , where
, where 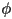 is the angle between
is the angle between 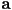 and
and 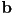 in radians
in radians

- proof (2D):
- identity does hold in any dimension greater than 1
- so
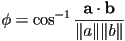 (this will typically return the smaller absolute angle between the vectors)
(this will typically return the smaller absolute angle between the vectors) - corollary 1: the component of
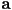 in the direction of
in the direction of 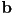 is
is 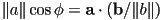 , or just
, or just  when
when 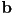 is a unit vector
is a unit vector
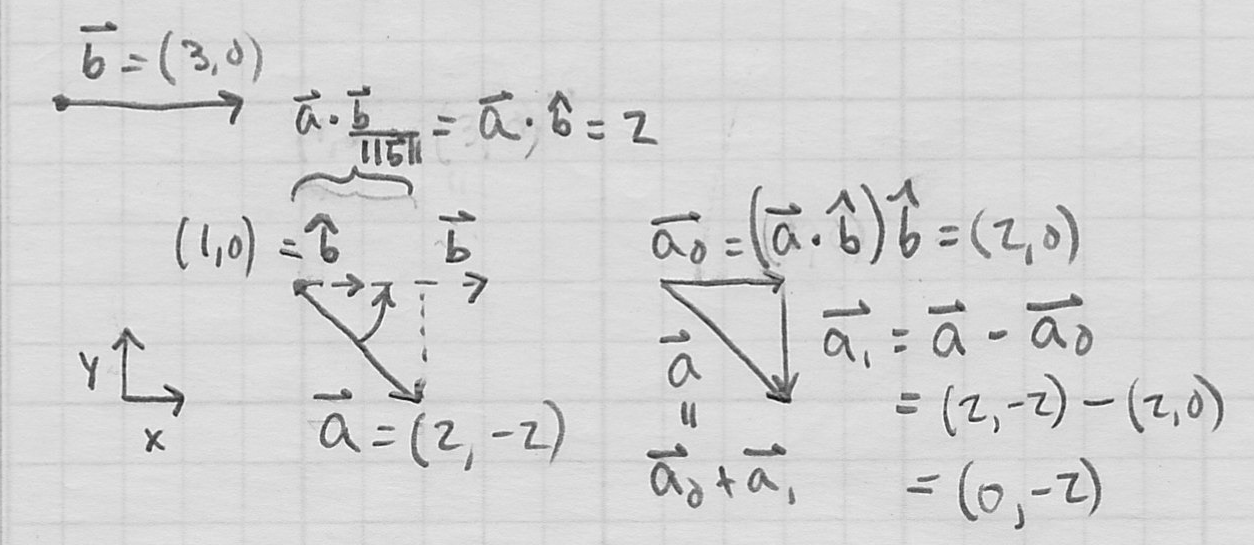
- corollary 2:
 implies
implies 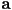 and
and 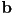 are perpendicular (assuming neither are
are perpendicular (assuming neither are 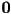 ), and vice-versa
), and vice-versa
- dot product is commutative and distributive
- “vector” or “cross” product:
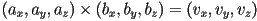
- inputs (factors): two 3-dimensional vectors
- output (product): a new 3-dimensional vector
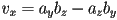
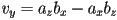
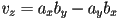
- geometrically,
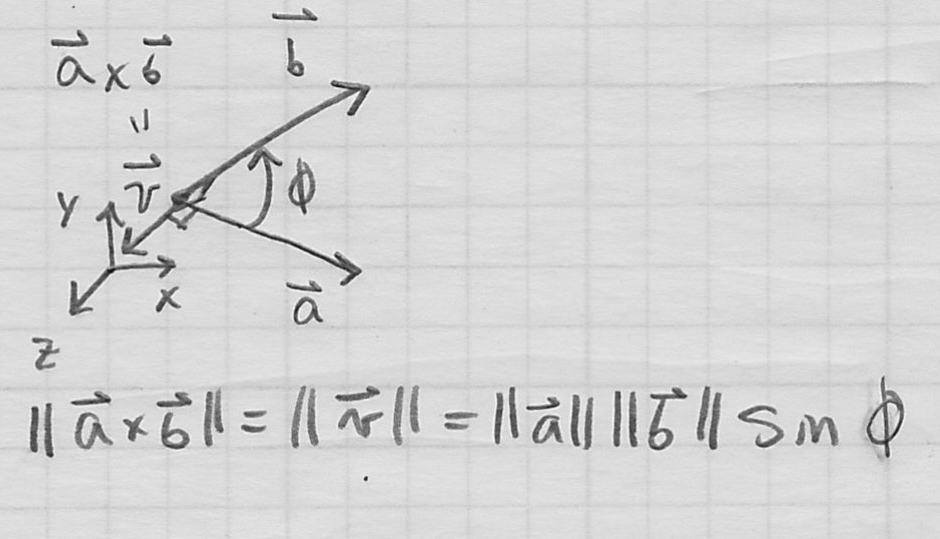
- the magnitude of
 is
is 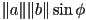 , where
, where 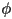 is again the angle between
is again the angle between 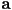 and
and 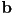 in radians
in radians - corollary:
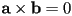 implies
implies  and
and  are either parallel or antiparallel (assuming neither are
are either parallel or antiparallel (assuming neither are 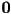 ), and vice-versa
), and vice-versa - but what is the direction of
 ?
? - possibly most useful property of cross product in graphics: if
 is not
is not 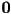 , then it is perpendicular to both
, then it is perpendicular to both 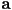 and
and 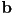
- but there are generally two options
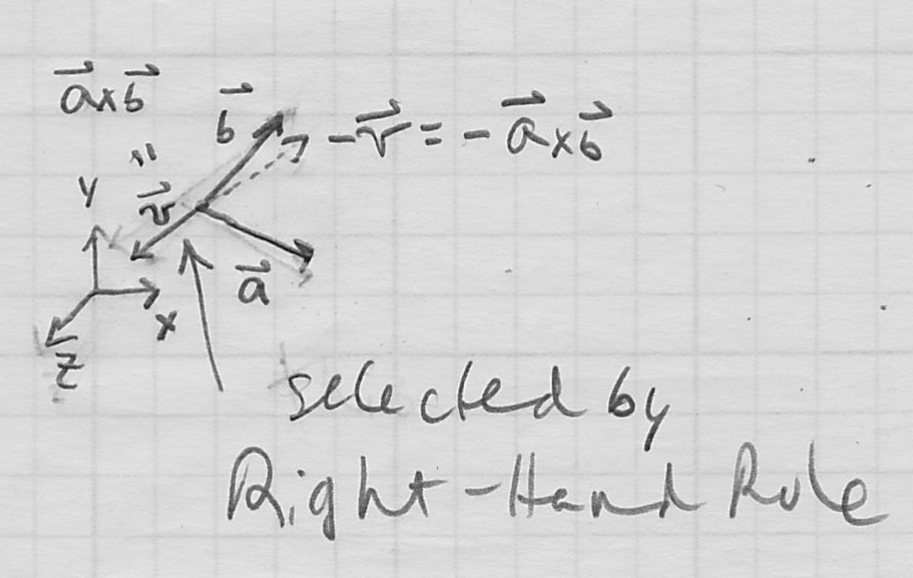
- cross product always picks the result
 defined by the right hand rule
defined by the right hand rule- align your right hand palm and fingers with
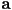
- curl your fingers in the direction of
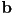
- stick out your thumb: that is the direction of
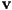
- what if you started with
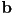 instead of
instead of 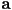 ?
?- demonstrates that cross product is not commutative:
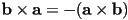
- cross product is common in 3D but also useful in a few cases in 2D
- one application in 2D is determining the side of a line segment on which a point falls (later)
- also sometimes useful to find a vector
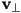 perpendicular to a given vector
perpendicular to a given vector 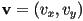 in 2D
in 2D- treat
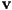 as a 3D vector with
as a 3D vector with 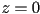
- compute
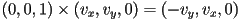
- so
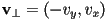
- There is no good way to define the multiplicative inverse of a vector, or division by a vector.
Next time
- coordinate frames
- points, segments, rays, and lines in 2D
- reading on website
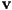 ), or handwritten with over-arrow (e.g.
), or handwritten with over-arrow (e.g.  )
)
 , etc
, etc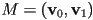
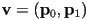
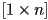 matrix
matrix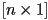 matrix
matrix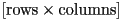
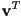 flips row vector into column vector and vice-versa, e.g.
flips row vector into column vector and vice-versa, e.g. 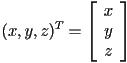
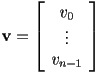 is written as
is written as 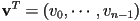 just to be more compact on the page
just to be more compact on the page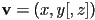
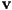 can represent a “location” (“position” or “point”), when reference point is the origin
can represent a “location” (“position” or “point”), when reference point is the origin 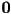
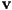 can also represent “offset” or “displacement”
can also represent “offset” or “displacement”
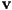 can also just be used to define a direction
can also just be used to define a direction