DUE: 12pm, Wed Mar 24
Worth: 7.5% of your final grade
This assignment is separated into three parts. Your handin will need to have a separate executable for each part, but some parts will likely be best implemented by re-using code you wrote in prior parts. For full credit, you must organize your work so that code shared between parts is not copied and pasted. For example, in Java you could write the code for the earlier part as a class C and then extend that class for the later part. [It is ok to update the implementation of C as you work on the later part as long as it also still works correctly for the earlier part.]
Many aspects of this assignment, such as triangle rasterization with barycentric interpolation and coordinate transformations, may be available as functions in various 2D and 3D graphics libraries. You are allowed to use any such library you like, subject to the course policies on third-party code. Of course, it will be up to you to make sure the library you choose is actually capable of performing exactly the required functions, and that you are using it correctly. For this relatively basic 3D assignment it is likely to be nearly as easy to write all the required code on your own as it will be to learn and correctly use a library.
All parts of this assignment will require your program to read an ASCII text input file that describes a list of triangles. Each line of the file specifies the vertex coordinates and vertex colors of one 3D triangle in the order
The coordinates of vertex 
are 
and the RGB color is 
.
All values are whitespace separated (one or more spaces or tabs) and given in ASCII floating point in the following format: (a) an optional leading + or - symbol; (b) between 1 and 4 decimal digits; (c) an optional fractional part consisting of a decimal point and between 1 and 4 decimal digits.
Your program must ignore any lines that begin with the # character.
All vertex coordinates are in units of floating point pixels. For rasterizing, you can round fractional pixels in the input to the nearest integer.
The 
color components range from 0.0 (none of that color) to 1.0 (full brightness of that color). Any color component that is (incorrectly) specified in the input as less than 0.0 should be treated as 0.0; any color component that is specified as greater than 1.0 should be treated as 1.0.
Some example input files are given below.
You may either
For example, if the input file is named “triangles.tri”, either of the following implementations is acceptable (these lines also assume a Java program called HW4_Sample, but the form is similar for other languages):
java HW4_Sample triangles.tri
or
java HW4_Sample < triangles.tri
(or just bring up a filechooser when your program starts).
Write a program to display a list of colored triangles in 2D with barycentric interpolation.
For this part, ignore the vertex 
coordinates in the input file (treat them as 0).
Your program must open a window with a drawing canvas of at least 512 by 512 pixels. Implement a “paint” function as usual to render the triangles on the canvas.
Your program must display the triangles in a 2D coordinate frame with origin at the center of the window, 
right, and 
up.
Barycentric interpolation must be used to determine the color of each pixel within a triangle.
Do not assume that the vertices for a triangle are specified in counterclockwise order. Your program must ignore any triangle whose vertices are not CCW in 2D. If the vertices of a triangle are 
, then one way to check if they are in CCW order is to compute 
and then check if 
. Note that you may treat the original vertex coordinates as zero for this computation, or you may keep them as given in the input file. It will work either way, because the component of the cross product depends only on the 
and 
components of the factors.
Your program must correctly handle clipped triangles that are either partially or fully outside the drawing area.
You may ignore degenerate triangles that would rasterize as a single line segment, or even as a single point. For such a triangle, 
, thus it is not possible to reliably determine whether the vertices are CCW.
For extra credit, ensure single ownership of pixels along the boundary between adjacent triangles.
Write a program to display a list of triangles in 3D with wireframe rendering, backface culling, and interactive rotation and scaling.
Your program must open a window with a drawing canvas of at least 512 by 512 pixels. Implement a “paint” function as usual to render the triangles on the canvas.
Your program must display the triangles in a right-handed 3D coordinate frame with origin at the center of the window, right, up, and 
pointing out of the screen.
Implement orthographic projection by rendering one 2D triangle 
for each 3D triangle 
where the vertices of are the same as the vertices of , but with cordinates ignored (set to zero).
This program renders each triangle in wireframe, i.e., it only rasterizes pixels that lie on the edge of a triangle. You may render the lines in any color you like. For extra credit, linearly interpolate vertex colors along the edges (note that this is equivalent to barycentric interpolation for those pixels).
Implement interactive rotation and scaling (of all triangles) about the 3D origin. You must at least implement two orthogonal axes of rotation as well as a uniform scaling, all bound to keyboard events. For example, when the user hits the right arrow all triangles could be rotated by a small increment (say 5 degrees) CCW about . The left arrow key would do the opposite, and the up and down arrow keys would rotate about . Hitting + could increase the scale, and - could decrease it. For extra credit you may also implement translation and/or using the mouse in addition to the keyboard.
You must cull (not render) backfacing triangles. For each triangle compute 
exactly as above. But here, you must compute based on the vertex coordinates after transforming them by the current rotation and scale. A 3D triangle is backfacing iff 
, i.e., if its projection onto the 2D 
plane is not in CCW order.
For this part, you must still correctly handle clipped triangles, and you may still ignore degenerate triangles. Single ownership is again extra credit.
Write a program to display a list of triangles in 3D with flat shading, barycentric interpolation, backface culling, and interactive rotation and scaling.
All of the requirements of part II also apply to this part, except that instead of wireframe rendering, you will perform flat shading with respect to a directional light source producing parallel rays of white light in the direction 
.
Let the vertices of a triangle be and let the corresponding specified vertex colors be 
.
Compute (not ignoring coordinates). The triangle is degenerate iff , and you may ignore it. Otherwise, compute 
.
Compute 
. The triangle is backfacing iff 
. Otherwise, compute 
for each of the original vertex colors and rasterize the triangle using barycentric interpolation of 
.
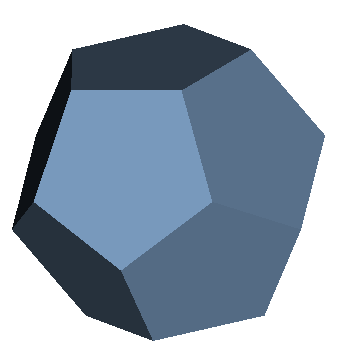
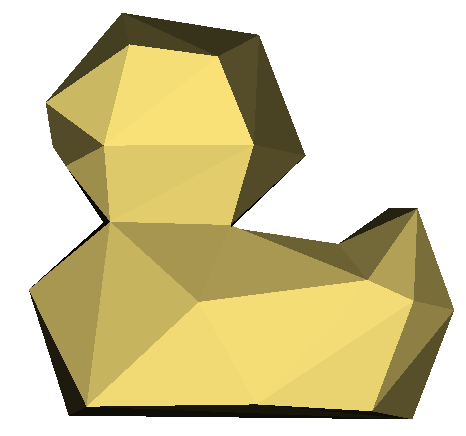
The following two were converted from original models found on the web, first with MeshLab and then with STLtoTRI.java.
Follow the instructions on the assignments page.
Be sure to document in your README file
Out of 100 total possible points, 60 will be assigned based on the organization, functionality, clarity, and documentation of your code. 20 will be assigned based on the graphic output of your program, and the remaining 20 will be based on the interactive features, including object rotation and zoom.