Lecture 11: Intro to Performance
1 A performance problem
In Assignment 1, your Duration.format(String)
method likely had to accumulate a string character by character in a
loop. Stripped down to its essence, building the string might have
looked something like this:
String result = "";
for (...) {
...
result += ...;
...
}
return result;That is, the most straightforward thing to do, when we need to
accumulate a string, is often to build it up character-by-character via
string appends. Naively, we might expect this to be quite efficient: after
all, the loop is doing a constant amount of work each iteration —
Unfortunately, this analysis is too simplistic: the actual performance of this
approach scales terribly. For example, here is are benchmark results for an
implementation of the format method on template strings of length 1000,
2000, 3000, and 4000, with two different "densities" of % signs ($\frac
1 4$ versus $\frac 1{50}$):
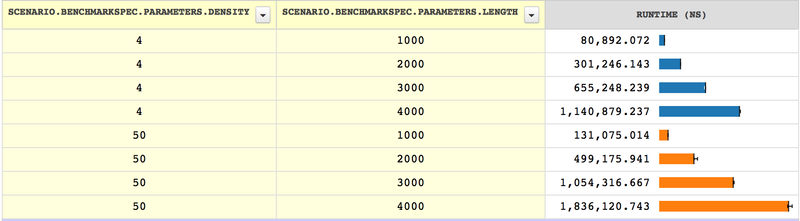
The lines represent running time, so longer lines are worse. As we can
see, the running time of this method superlinearly—
Somehow, what seemed like a single, cheap operation isn’t.1In
fact, it’s usually quite subtle to determine the actual expense of a given
operation. The accuracy of our so-called cost model is essential in
predicting the performance of our application. And costs can vary enormously,
by factors of a million or more! For a useful intuitive explanation of a very
low-level cost model for a machine, see
https://gist.github.com/hellerbarde/2843375. To see why we’re getting
such bad performance, we need to consider what is happening under the hood. In
Java (and many programming languages), a string is represented as an array of
characters. The Java String class is immutable, which means that when we
append two strings, it allocates a fresh, new String object to hold the
result. Under the hood, this entails allocating a new array with enough space
to hold the characters from both strings, and then copying the contents into
it. This operation takes time proportional to the length of the resulting
string. When we accumulate a string in a loop, this means that we are
allocating a new string in each iteration of the loop, and the size of that new
string increases each time. Overall, to accumulate a string of length $n$,
character by character, this will do $n$ copies, allocating new strings of
length 1, 2, $\ldots$, $n$. Adding this up, we get the time $T(n)$ to
accumulate a string of length $n$,
$$ T(n) = \sum_{i = 1}^n ci = c\frac{n(n + 1)}{2}\,, $$
where $c$ represents some constant factor involved in each operation
(since the exact time to allocate a string and copy its contents depends
on details of the particular machine and environment in which we are
running). Because the above expression is quadratic in $n$, this
explains why our format method scales superlinearly.
2 A mathematical digression
You likely have previously seen the formula above, stating that the sum of the first $n$ numbers is $\frac{n(n+1)}{2}$. Take a moment to consider how to prove such a formula. Here is one common proof:
When $n = 1$, $\sum_{i = 1}^1 = \frac{1(1+1)}{2} = 1$. So our base case is satisfied.
Assume inductively that the formula holds for $n$; show that it works for $n+1$:
$$ \begin{align*} \sum_{i=1}^{n+1} i &= \left(\sum_{i = 1}^n i\right) + (n+1) \\ &\text{by induction} \\ &= \frac{n(n+1)}{2} + (n+1) \\ &= \frac{n(n+1)}{2} + \frac{2(n+1)}{2} \\ &= \frac{(n+2)(n+1)}{2} \end{align*} $$
This proof is straightforward, fairly simple...and utterly unenlightening: how
did we guess the appropriate formula in the first place? Moreover, suppose we
needed to solve a related problem (such as $\sum_{i=1}^n i^2$, or higher
powers) —
Another common proof, due to Carl Friedrich Gauss, goes as follows: pair off the first and last numbers of the range, the second and next-to-last numbers, etc:
$$ \begin{align*} 1 \qquad& n\\ 2 \qquad& n-1\\ 3 \qquad& n-2 \\ \vdots\qquad&\vdots \\ \mathrm{floor}(n/2) \qquad& \mathrm{ceil}(n/2) \end{align*} $$
Each row sums to $n+1$, and there are $\frac{n}{2}$ rows. Therefore the total sum is $\frac{n(n+1)}{2}$ as desired.2Unless $n$ is even, in which case the last row sums to $n$ itself...but dividing it by 2 will result in the correct result anyway. This proof is a bit better: you don’t have to know the formula in advance in order to derive it, but you need some insight to see that arranging the numbers in this manner will be helpful.
Here is an alternate proof I first learned in high school, which at first seems totally pointless, but works its way around to a very elegant result. Consider the well-known fact
$$ (n+1)^2 = n^2 + 2n + 1 $$
Now comes an odd observation —
$$ (n)^2 = (n-1)^2 + 2(n-1) + 1 $$
Why bother with this? Because we can continue in this manner all the way down:
$$ \begin{align*} (n+1)^2 &= (n-0)^2 + 2(n-0) + 1 \\ (n-0)^2 &= (n-1)^2 + 2(n-1) + 1 \\ (n-1)^2 &= (n-2)^2 + 2(n-2) + 1 \\ &\vdots \\ 1^2 &= (n-n)^2 + 2(n-n) + 1 \\ \end{align*} $$
Now we can apply something like Gauss’s technique, and sum all these equations together. But notice: most of the terms cancel each other out, because they appear on both sides of the equals signs. We are left with
$$ (n+1)^2 = 2\left((n-0) + (n-1) + \cdots + (n-n)\right) + \left(1 + 1 + \cdots + 1\right) $$ Or in other words, $$ (n+1)^2 = 2\left(\sum_{i=1}^n i\right) + (n + 1) $$ With just a little bit of algebra, we obtain the desired formula...without knowing in advance what the formula should be.
Better yet, we can generalize this technique: $$ \begin{align*} (n+1)^3 &= (n-0)^3 + 3(n-0)^2 + 3(n-0) + 1 \\ (n-0)^3 &= (n-1)^3 + 3(n-1)^2 + 3(n-1) + 1 \\ (n-1)^3 &= (n-2)^3 + 3(n-2)^2 + 3(n-2) + 1 \\ &\vdots \\ 1^3 &= (n-n)^3 + 3(n-n)^2 + 3(n-n) + 1 \\ \end{align*} $$ Again terms cancel, and we get $$ (n+1)^3 = 3\left(\sum_{i=1}^n i^2\right) + 3\left(\sum_{i=1}^n i\right) + (n+1) $$ Conveniently, we can reuse the solution we just got for the second sum, and with a bit of algebra obtain the final formula for this form as well.
Or in other words, with a bit of refactoring3Quite literally!, we can take a formula that was only of utility in one limited situation and instead obtain a proof technique that can be reused to solve several related problems.
Analogously, finding the right spot in your program to refactor can lead to a profoundly useful point of leverage from which to improve your code. Let’s see how we might apply similar reasoning to our example string-appending problem above.
3 Abstracting the problem
In order to try other strategies for accumulating the string, we will now
abstract our format(String) method over the string accumulation
process. In particular, we define an interface for objects that provide a
string accumulation service. The
full interface
provides several more useful methods, but to start out we need only two:
public interface StringAccumulator {
/**
* Appends the given character to the end of the accumulated string.
*
* @param c the character to append
* @return a reference to {@code this} (for method chaining)
*/
@Override
StringAccumulator append(char c);
/**
* Returns the accumulated string value. Should be the same as
* {@code #toString()}.
*
* @return the accumulated string value
*/
String stringValue();
}The idea is that using an object of a class that implements
StringAccumulator, we can repeatedly append characters, potentially
allowing the object to manage the accumulation in a more efficient way
than repeated string appends, and then when we’re done, extract the
resulting string4Can you see a similarity with the builder pattern
here?:
StringAccumulator result = new ...StringAccumulator();
for (...) {
...
result.append(c);
...
}
return result.stringValue();In order to demonstrate that our approach is sound, we first implement the interface in a class that uses the same string-appending technique that gave us the bad performance above:
/**
* A string accumulator implementation that just stores the string. This is
* very simple to implement but will suffer the same poor performance as
* naive string appending.
*/
public final class StringStringAccumulator implements StringAccumulator {
private String contents = "";
@Override
public String stringValue() {
return contents;
}
@Override
public StringStringAccumulator append(char c) {
contents += c;
return this;
}
}Of course, the above does not make our code run any faster, but it enables us to run our tests and ensure that abstracting over string accumulation doesn’t break our existing code. Once we know that is the case, we can try to implement the interface in a way that improves our string accumulation performance.
4 Improving our technique
The key to improving our string accumulation performance is to avoid
allocating and copying each time the append(char) method is
called. Instead, we will accumulate characters in an array, which we may
allow to be larger than is necessary to hold the characters accumulated
thus far. By trading space for time, we hope to speed up duration
formatting.
We start by writing an ArrayStringAccumulator class that uses
a character array, rather than a String, to hold the characters:
public class ArrayStringAccumulator implements StringAccumulator {
private char[] contents = new char[INITIAL_CAPACITY];
private int length = 0;
}In this class, in addition to the char[] field contents
holding the characters, we need the length field to keep track of how
much of contents is currently filled with characters that we have
accumulated. This will allow us to use an array that is not yet full, so
that we can add more characters without reallocating and copying.
Initially, contents points to a freshly allocated character array of
some capacity (which doesn’t particularly matter, so long as it isn’t
really large), and the length starts out at 0. We then have two public
methods to implement.
In order to get the accumulated String value, method
stringValue() initializes a new string to the valid prefix of
the array and returns that:
@Override
public final String stringValue() {
return String.valueOf(contents, 0, length);
}The static String#valueOf(char[], int, int) method takes a
character array, the offset where the new string should start, and a
count of characters to include. We want the first length characters of
array contents.
We also need to implement the append(char) method, which adds a
character to the end of the buffer. The buffer may or may not have to
grow before we can add a character to it, so we will delegate to a
private helper ensureCapacity(int) that expands the array to the
requested capacity if necessary:
@Override
public final ArrayStringAccumulator append(char c) {
ensureCapacity(length + 1);
contents[length++] = c ;
return this;
}The method ensures that we have room for one additional character, then
stores it at the end of contents and increments the length field to
record the fact that we have added a character. It returns
this as required by the StringAccumulator interface.
Now we need to implement ensureCapacity(int). We will express
only a small amount of the growing logic here, delegating to two other
methods to decide what size to expand to, and to do the expansion
itself:
/**
* Resizes the underlying array, if necessary, to ensure that the capacity
* exceeds the specified {@code minCapacity}.
*
* @param minCapacity lower bound for the new capacity
*/
public final void ensureCapacity(int minCapacity) {
if (contents.length < minCapacity) {
resize(determineNewCapacity(minCapacity));
}
}If the capacity of the underlying array is sufficient to hold
minCapacity characters, there is no need to expand. Otherwise,
we delegate to method determineNewCapacity(int) to decide what size to
grow to, and then to method resize(int) to do the actual
growing. Method resize(int), in turn, can delegate to the
static Arrays.copyOf(char[], int) method, which makes a copy of
an array of the requested size:
/**
* Resizes the underlying array to the given capacity.
*
* @param newCapacity the new capacity of the array
*/
private void resize(int newCapacity) {
contents = Arrays.copyOf(contents, newCapacity);
}It remains to implement the determineNewCapacity(int) method, which
determines what size to expand array contents to when expansion is
necessary. (If we expand only to the needed capacity, we have
merely reimplemented the nonperformant version of string accumulation
that we started with. We’ll try that, among other things, just to be
sure.) Because we would like to try a variety of array expansion
strategies, we will abstract over this decision.
5 Abstracting the expansion strategy
Rather than implement one ArrayStringAccumulator class with a
fixed expansion strategy, we will change the above to an abstract base
class
AbstractArrayStringAccumulator,
which defers the implementation of the
determineNewCapacity(int) method, and thus the expansion
strategy, to its concrete subclasses. Thus, we rename class
ArrayStringAccumulator to AbstractArrayStringAccumulator. Here is
the whole class at this point5Note that the full version linked in the
previous sentence is more comprehensive, but rather than explain the
details here, I summarize some of the differences near the end of this
lecture and leave understanding the details as an exercise for the
reader.:
public abstract class AbstractArrayStringAccumulator
implements StringAccumulator
{
private char[] contents = new char[INITIAL_CAPACITY];
private int length = 0;
/**
* The initial array capacity.
*/
public final static int INITIAL_CAPACITY = 10;
@Override
public final String stringValue() {
return String.valueOf(contents, 0, length);
}
@Override
public final String toString() {
return stringValue();
}
@Override
public final ArrayStringAccumulator append(char c) {
ensureCapacity(length + 1);
contents[length++] = c ;
return this;
}
/**
* Returns the current capacity of the string accumulator, after which
* expansion will be necessary.
*
* @return the current capacity
*/
public int capacity() {
return contents.length;
}
public final void ensureCapacity(int minCapacity) {
if (contents.length < minCapacity) {
resize(determineNewCapacity(minCapacity));
}
}
private void resize(int newCapacity) {
contents = Arrays.copyOf(contents, newCapacity);
}
/**
* Returns the capacity to expand to, given the requested minimum
* capacity.
*
* @param minCapacity the requested minimum capacity
* @return the capacity to expand to
*/
protected abstract int determineNewCapacity(int minCapacity);
}In order to implement a concrete StringAccumulator class, it
thus suffices to extend AbstractArrayStringAccumulator and
override the determineNewCapacity(int) method to implement a
particular expansion strategy. Note that we added a method
capacity() in order to allow subclasses to find out the current
capacity, since the actual representation array contents is
private. (We don’t want subclasses to be able to mess with our
invariants!)
5.1 Four strategies for growing
Now we can try several strategies for growing the array, and use
benchmarks to compare them. Unsurprisingly, will first reimplement the
naïve strategy of keeping the array at the exact size needed. (If
nothing else, this continues to provide proof of concept for our
abstractions.) We call this class
ExactArrayStringAccumulator;
if our understanding of the problem is correct, this will give us the
same poor performance that we started with:
/**
* A string accumulator class that always expands to exactly the
* necessary size to hold the current accumulated character sequence.
*/
public final class ExactArrayStringAccumulator
extends AbstractArrayStringAccumulator
{
@Override
protected int determineNewCapacity(int minCapacity) {
return minCapacity;
}
}Since we hypothesized that the source of the poor performance was
frequent array expansions, one reasonable strategy might be to expand
the array some larger but fixed step at a time. The strategy of class
LinearArrayStringAccumulator
is to expand to the smallest multiple of DEFAULT_STEP that will
hold the requested minimum capacity:
public final class LinearArrayStringAccumulator
extends AbstractArrayStringAccumulator
{
public static int DEFAULT_STEP = 16;
@Override
protected int determineNewCapacity(int minCapacity) {
// (a + b - 1) / b computes ceil((double) a / b)
return ((minCapacity + DEFAULT_STEP - 1) / DEFAULT_STEP) * DEFAULT_STEP;
}
}If we consider LinearArrayStringAccumulator carefully, we may
notice that it still expands a linear number of times to build a
string—DoublingArrayStringAccumulator:
public final class DoublingArrayStringAccumulator
extends AbstractArrayStringAccumulator
{
@Override
protected int determineNewCapacity(int minCapacity) {
return Integer.max(minCapacity, capacity() * 2);
}
}As a final strategy, we might elect to allocate a sufficiently large array that
expansion is unnecessary, at least in the cases where we know how large an
array we are going to need. The version of
AbstractArrayStringAccumulator that we just wrote does not provide a way
for subclasses to influence the initial array size (though the
full
version here does). However, we can approximate this behavior up to a point
by returning a sufficiently large value from determineNewCapacity(int)
such that none of our benchmarks exceed it, and we will thus get exactly one
reallocation, regardless of how large the string must grow. (The risk here is
that this allocation is so large that it hurts our performance, but if that is
the case, the benchmarks will show it.)
public final class PreallocArrayStringAccumulator
extends AbstractArrayStringAccumulator
{
@Override
protected int determineNewCapacity(int minCapacity) {
return Integer.max(minCapacity, 100_000);
}
}5.2 Benchmarking the strategies
Now that we have four strategies for growing the array, we would like to
compare them. The benchmarks in
StringAccumulatorBench
build strings of several sizes using our array-growing strategies.
Here are the results:
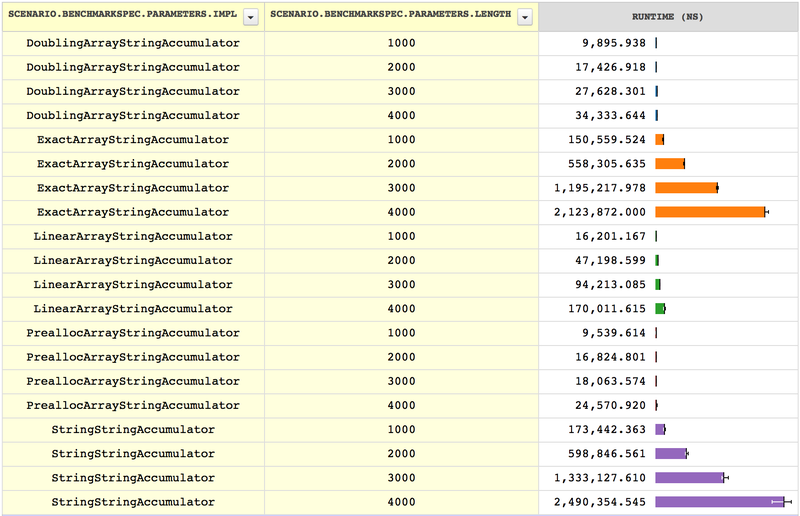
As we can see, StringStringAccumulator and
ExactArrayStringAccumulator perform very similarly to our
original implementation of the format method, which is unsurprising,
since each of them expands the string or array each time a character is
added. The other implementations all look significantly faster but
similar to each other, but if we want to see the difference between the
linear-step strategy, the doubling strategy, and the prealloc strategy,
then we need to try larger cases. In this benchmark, we increase the the
size of the accumulated strings by a factor of 10:
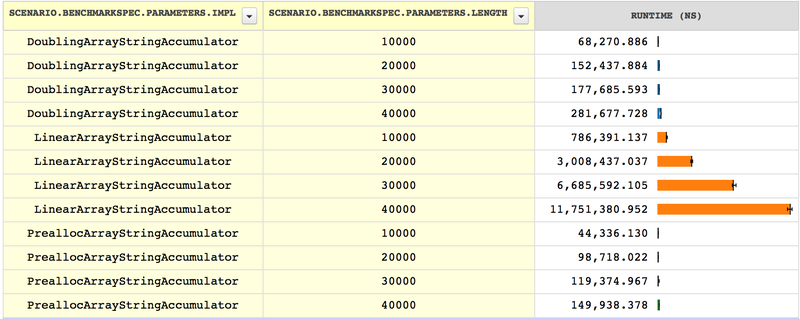
Now we can see that LinearArrayStringAccumulator’s growth is
similar to StringStringAccumulator’s and
ExactArrayStringAccumulator’s, only with better constant
factors. Expanding the string less often by a constant factor means that
the growth in time has the same shape, merely scaled down (or starting
from a smaller baseline). But eventually, for large enough strings, the
strategy taken by LinearArrayStringAccumulator will become
nonperformant. The doubling and prealloc strategies, on the other hand,
are inherently linear, and no matter how much we expand, the time they
take will be proportional to the size of the string they are building. The
prealloc strategy may be faster by some constant factor, but with a
significant decrease in flexibility, since it requires choosing a size
up front.
6 Applying our results
Now that we have a good idea how our various expansion strategies
perform, we should verify that they work not only when benchmarking
mere string accumulation, but in the context for which we intended
them, the duration format method. Here is a benchmark comparing our
string accumulation classes with each other and with two classes from
the Java library, StringBuilder and StringBuffer6What
we have done here is, in fact, a simple reimplementation of Java’s
StringBuilder. StringBuffer is similar—StringBuilder.:
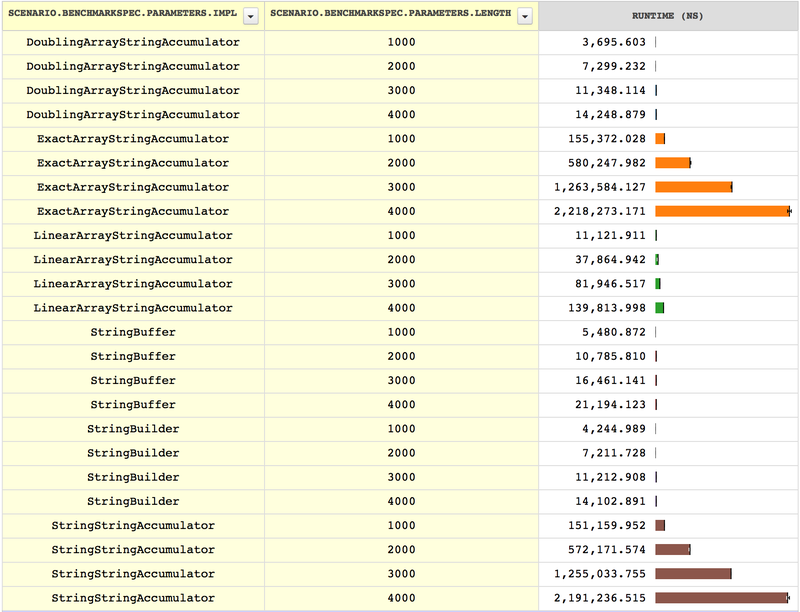
As we can see, our string accumulation benchmark was valid for predicting the performance of a duration formatting benchmark (though whether that validity extends to "real-world" duration formatting is another question, which we won’t attempt to answer here).
7 Differences between the code in this lecture and the full version that I’ve been linking to
The code in this lecture is simplified from more comprehensive implementations of the same classes, which I have linked throughout. The differences are:
The full
StringAccumulatorinterface includes methods for appending not only single characters butCharSequences, which is an interface that includesStrings and other ways to represent (sequences of) characters.The full
StringAccumulatorinterface extends the interfaceAppendablefrom the Java library.Appendablespecifies a similar concept (but is slightly more complex). ExtendingAppendableis what allows us to use the same benchmarking code for our classes and for Java’sStringBuilderandStringBuffer, since those implementAppendableas well.The full version of
AbstractArrayStringAccumulatordefines a methodinitialCapacity(), which subclasses can override to choose a different initial capacity for the array than the default. ThePreallocArrayStringAccumulatorclass overrides this method in order to preallocate a large array more elegantly than we did above.
8 Conclusion
This is merely an introduction to performance. In the next lecture, we will see how to reason about resource usage more formally, using the concept of asymptotic complexity and big-O notation.
1In fact, it’s usually quite subtle to determine the actual expense of a given operation. The accuracy of our so-called cost model is essential in predicting the performance of our application. And costs can vary enormously, by factors of a million or more! For a useful intuitive explanation of a very low-level cost model for a machine, see https://gist.github.com/hellerbarde/2843375.
2Unless $n$ is even, in which case the last row sums to $n$ itself...but dividing it by 2 will result in the correct result anyway.
4Can you see a similarity with the builder pattern here?
5Note that the full version linked in the previous sentence is more comprehensive, but rather than explain the details here, I summarize some of the differences near the end of this lecture and leave understanding the details as an exercise for the reader.
6What
we have done here is, in fact, a simple reimplementation of Java’s
StringBuilder. StringBuffer is similar—StringBuilder.