Lecture 2: Logistics, Specifications in LSL
1 Purpose
Cover course policies, start with LSL
2 Outline
Introduce yourself to neighbor!
Sign up for Discord. IMPORTANT: Must set your display name for the server to your Full Name before we give you access to the course channels. All class communication will go through Discord.
Bring computer to class! We’ll often write things in class.
Install DrRacket, if you don’t have it already. Update it if it’s below 8.15
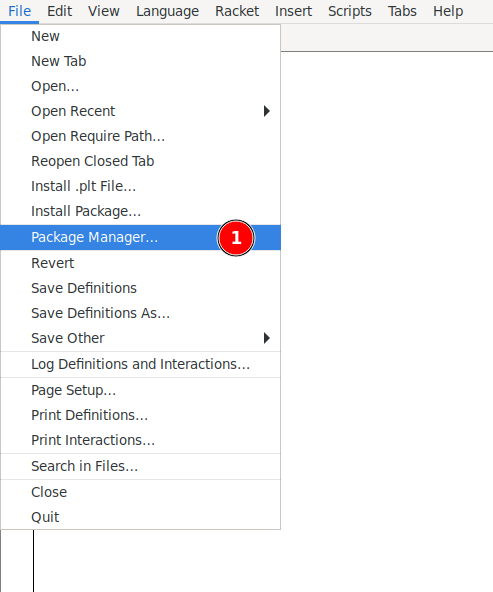
Install Logical Student Language
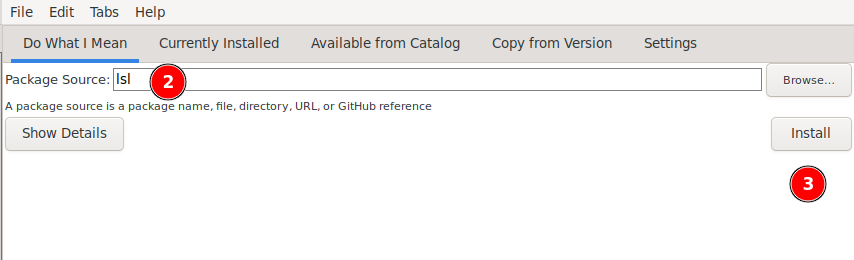
You can install it from within DrRacket by going to File -> Package Manager..., and then searching for lsl.
Switch to "Determine Language from Source" at the bottom left (to get this option, you may need to click "Choose language" and then choose "The Racket Language") and begin each file with "#lang lsl".
Documentation for LSL is available at:
https://docs.racket-lang.org/lsl/
This language is (essentially) extension of the the Intermediate Student Language with Lambda (ISL+) language from Fundies 1, with a lot of features for logical reasoning.
If you need review of ISL+ – see ISL+ Recap. If you want more:
If you’d rather watch videos, these are a concise presentation of most of what was in Fundies 1:
https://users.cs.utah.edu/~mflatt/htdp-lite/
Syllabus!
Important details: grading allocation, HW collaboration policies, etc.
(covered in some detail)
Office hours
Start today. Almost all in-person; one (on Monday) is online. In addition to TAs, instructors have office hours.
Homework
One assignment per week, due Thursday by MIDNIGHT . All problems all autograded. Homework in this class is the primary way that you will learn the material, so we want the feedback loop to be tight.
Start experimenting with LSL
Set "Determine Language from Source" at bottom left, write #lang lsl at top of file, write some simple functions.
In addition to (most of) the features from ISL+, LSL adds a couple ones. We’ll start, however, using something you should remember from Fundies 1:
(check-expect (f1 10 2) 12) 1 success(es) 0 failure(s) 0 error(s) 1 test(s) run
We’ll learn quite a bit more about testing this semester, and how to go much further than just unit tests, but unit tests will remain useful. One different perspective: if you write predicates (boolean-returning-functions) on the output and use those in your unit tests instead, you can write tests in a slightly different way:
; my-abs : Number -> Number ; takes absolute value of number
(define (my-abs x) (if (< x 0) (* x -1) x)) ; nonnegative? : Number -> Boolean
(define (nonnegative? x) (or (= x 0) (positive? x)))
(check-satisfied (my-abs 10) nonnegative?) (check-satisfied (my-abs -5) nonnegative?) (check-satisfied (my-abs 0) nonnegative?) 3 success(es) 0 failure(s) 0 error(s) 3 test(s) run
check-satisfied is in ISL+, though you may not have used it. This snippet of code, simple as it is, is our first example of a formal specification. What we are expressing, formally, is that the result of my-abs should be non-negative.
It is formal because it is expressed in unambiguous language: in this case, in executable LSL code. And it is a specification because it is an abstracted, higher level description of the behavior of the program. Hopefully, that has utility to someone who wants to use or understand the code. Purpose statements, what you are familiar with, are informal specifications: they similarly convey meaning to people who want to use or understand the code, but they are informal because they lack precision.
Why do you think we prefer formal to informal specifications?
Answer: precision is useful, but can come at a cost of complexity. But, the benefit is that we can often actually connect them to the code we run, as above. Not only are we expressing that the result should be non-negative, we are validating that on a set of inputs.
Now, we could have written the above as typical unit tests instead:
(check-expect (my-abs 10) 10) (check-expect (my-abs -5) 5) (check-expect (my-abs 0) 0) 3 success(es) 0 failure(s) 0 error(s) 3 test(s) run
What do we lose? Nowhere do we indicate that we intend that the output is always nonnegative.
Perhaps a reader would understand from the behavior that this is what is going on, and an informal specification (a purpose statement) would go a long way to helping. Another advantage of expressing the property we wish to hold in executable form is that if the reader is skeptical of our set of tests (i.e., they wonder if our property holds of the input -42), they can easily add that test:
(check-satisfied (my-abs -42) nonnegative?) 1 success(es) 0 failure(s) 0 error(s) 1 test(s) run
That’s not the case with just unit tests, as they need to figure out what should the function return on input -42 before they can write that test. Hopefully the informal specification (purpose statement) allows them to determine that, but that relies upon the purpose statement being really really clear.
Limitations of Unit Tests
Sometimes, there are functions we can write where we don’t want typical unit tests because they would constrain internal implementation details that shouldn’t be constrained. Let’s see an example:
; prime-factor-of : Number -> Number ; returns one of the prime factors of the input number. (define (prime-factor-of n) ...)
In other words, we are changing the function’s behavior, but keeping its interface (i.e., purpose) the same.
Even though we don’t know which prime factor prime-factor-of returns, we can still argue this is a correct primality checker. If the function returns true,
then prime-factor-of n must be equal to n —
(check-expect (prime-factor-of 3) 3) (check-expect (prime-factor-of 7) 7) ; Both tests below should be valid! ; (check-expect (prime-factor-of 10) 2) ; (check-expect (prime-factor-of 10) 5)
For 3 and 7, there is only one valid prime factor (the number itself), so the function’s behavior can be constrained by a unit test. However, for 10, there are two different inputs, and both are valid! We could choose one, but then we are overly specifying the behavior of the function, and therefore changing the function’s intention. Any choice of output for 10 could be wrong for a valid implementation of prime-factor-of. More generally, we often have problems that can be solved in many different ways, and we don’t want to prematurely limit the solution by specifying unit tests.
We can, and should, do better:
; prime-factor-of-prop : Number -> Boolean (define (prime-factor-of-prop n) (let* ([factor (prime-factor-of n)] [divides? (lambda (x y) (= (remainder y x) 0))] [prime? (lambda (x) (andmap (lambda (y) (not (divides? y x))) (range 2 (sub1 x) 1)))]) (and (divides? factor n) (prime? factor))))
Now, we’ve expressed exactly what we mean by "prime factor of": first, that it is a factor (in that it divides the input), and second, that it is prime (via an inefficient algorithm). Now, no matter how prime-factor-of is defined, provided it is correct, it should pass this specification. We can thus write tests using it, rather than as unit tests:
(check-expect (prime-factor-of-prop 3) #t) (check-expect (prime-factor-of-prop 7) #t) (check-expect (prime-factor-of-prop 10) #t)
Or, using check-satisfied:
(check-satisfied 3 prime-factor-of-prop) (check-satisfied 7 prime-factor-of-prop) (check-satisfied 10 prime-factor-of-prop)
Note that we wrote this specification slightly differently than we did the one for my-abs: this time, the assertions about the output depend on the input in a fundamental way. This meant that the call to prime-factor-of were inside the property.
Stepping back we will see lots of ways to write specifications this semester, and lots of ways to connect them to code, but the general pattern you already see will carry through all of it. The point of formal specification is to be precise (more precise than a purpose statement) and to be able to actually validate your specification.