Lab 3: Methods for Complex Data
Goals: The goals of this lab are to practice designing methods for complex data and to practice testing thoroughly.
For this lab, there are no starter files. Start a new project and build the file from scratch.
Using the javalib library
To use the library, download the javalib.jar file above and add it to your project the same way you have added the tester library.
At the top of the .java file where the library is used, add the following import statements:
import tester.*; // The tester library import javalib.worldimages.*; // images, like RectangleImage or OverlayImages import javalib.funworld.*; // the abstract World class and the big-bang library import java.awt.Color; // general colors (as triples of red,green,blue values) // and predefined colors (Red, Green, Yellow, Blue, Black, White)
The first one is familiar; the next three are needed to import the definitions from javalib.
1 Methods for complex data
Alexander Calder was an American artist well known for his hanging sculptures called mobiles. Look up some of his work; it is quite pretty.
We would like to help other artists who may want to design mobiles, so they can check ahead of the time whether their mobile will fit in the desired space (height, width, weight), and whether it will be properly balanced.
The following drawing shows two mobiles, one simple and the other more complex:
![]()
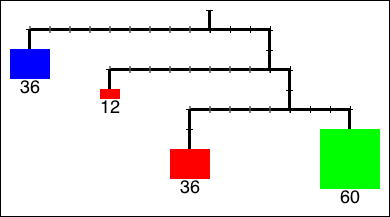
Each horizontal bar is a strut (a very thin, very lightweight rod), and each vertical bar is a string. We will restrict the mobile to two items hanging from each strut, and record for any item hanging at the end of the line its weight and its color.
We have decided on the following data representation for mobiles (the length refers to the length of the vertical string, the leftside and rightside refer to the two parts of the strut):
+---------+
| IMobile |<---------------+
+---------+ |
+---------+ |
| |
/ \ |
--- |
| |
--------------------- |
| | |
+--------------+ +---------------+ |
| Simple | | Complex | |
+--------------+ +---------------+ |
| int length | | int length | |
| int weight | | int leftside | |
| Color color | | int rightside | |
+--------------+ | IMobile left |----+
| IMobile right |----+
+---------------+Convert this data definition into Java interfaces and classes and make several examples of mobiles. Include in your examples at least three mobiles, the first two as shown above and the third one more complex that what is shown here. Name the examples exampleSimple, exampleComplex and example3, and your examples class ExamplesMobiles.
Design the method totalWeight for the mobiles that computes the total weight of the mobile. We assume that the weight of the struts from which the mobile hangs is negligible, as is the weight of the string on which the disks hang. For example, the total weight of the second mobile is 144.
Design the method totalHeight that computes the height of the mobile. Assume that the shapes in Simple mobiles have a height of their weight divided by 10 (rounded down). For example, the total height of the second mobile is 12.
Design the method isBalanced that computes whether a mobile is balanced. A given node is balanced if there is no net torque on the node, and torque is defined as the product of the weight of a node and the length of the strut to which it is attached. (The second example above is balanced.)
The remaining two problems are harder:
Design the method buildMobile that combines this balanced mobile with the given balanced mobile and produces a new mobile as follows:
The method is also given the desired length of the string on which the new mobile will hang, and the total length of the strut that will be used to hang the two mobiles. This mobile will be the left side; the given mobile will be the right side. Your job is to make sure that the length of the strut is divided into the left and right side in such way that the resulting mobile will also be balanced.
- Design the method curWidth that computes the current width of a mobile, i.e. where the left side of every complex mobile truly is on the left, the right side of every complex mobile truly is on the right, and nothing is spinning or otherwise...mobile. In essence, it’s the width of the mobile when it is laid flat against a wall. The width of a simple mobile is defined to be its weight divided by 10, rounded up to the nearest integer.
For those of you who are aware of Math.ceil, note that this function returns a double, not an int. You probably don’t want to use it here.
The width of a complex mobile is for you to figure out.