7 2/25: Java, Dictionaries, and the Internet
Download prima-1.2.3.jar from http://code.google.com/p/nutester.
Warmup: same data, different language
In this lab, we’ll be introducing you to designing interface, data, and class definitions in Java. If you follow the design recipe, the process is mostly the same, though you may have to think about types and Java syntax.
Think back to lab 5, in which we built several implementations of the Dictionary interface. In case you don’t remember, here’s the interface again, but in Java:
// A Key is a String
//
// A Dict<V> implements
//
// has-key : Key -> Boolean
// Does the given key exist?
//
// lookup : Key -> V
// The value mapped to by the given key
//
// set : Key V -> Dict<V>
// Set the given key-value mapping
Note that we have removed the assumption for lookup that the key is in the dictionary. It turns out that, unlike in class/0, Java forces us to implement lookup for all classes that implement the Dict interface.
throw new RuntimeException("Error message"); |
Exercise 1. Implement a Dict in Java using any of the designs from lab 5. Make sure to translate the data definition to the Java syntax first.
You may find the compareTo method on Strings useful for this exercise. The compareTo method takes an object that implements the Comparable interface (many built-in Java objects) and returns an int. This number is negative, zero, and postive respectively when the given object is less than, equal to, or greater than this.
There are several other operations that you might want in a good library for dictionaries. For example, you may want to be able to extract just the keys or values contained in a dictionary:
// keys : -> List<Key>
// return the keys in the dictionary
//
// values : -> List<V>
// return the values in the dictionary
List<X> above is an interface for a generic kind of list. Since Java has support for generic types, let’s take advantage of that and write down one data and class definition we can use for the results of both the keys and values methods.
// A List<X> is one of:
// - new Empty<X>()
// - new Cons<X>(X, List<X>)
//
// and implements:
//
// length : -> Integer
// The length of the list
//
// first : -> X
// The first element in the list (assumes list is non-empty)
//
// rest : -> List<X>
// The rest of the list (assumes list is non-empty)
Exercise 2. Define the List<X> interface and the Empty<X> and Cons<X> classes that implement it.
Now using the class definitions for lists, let’s flesh out our dictionaries.
Exercise 3. Implement the keys and values methods above.
Another thing you might want to do is run a function to update the value mapped by a particular key (instead of just providing the new value). Since Java doesn’t have higher-order functions, we will simulate them with objects. Here’s an interface defintion for a unary function from X to Y:
// A Fun<X,Y> implements:
//
// call : X -> Y
// Call this function on its X input and produce a Y
Let’s use this to define a new method for dictionaries.
// Dict<V> also implements:
//
// update : Key Fun<V, V> -> Dict<V>
// run the given function to get a new value for key
Exercise 4. Implement the update method.
One problem with the data definition above is that it only lets you use keys that are Nats. Since the only operation that we need for the key is that it lets us check if two keys are equal, let’s build that into our data definitions:
// An Eq implements
//
// equals : Eq -> Boolean
We chose the name equals because all of the built-in classes like Integer and String in Java implements it.
// A EqDict<V> implements
//
// has-key : Eq -> Boolean
// Does the given key exist?
//
// lookup : Eq -> V
// The value mapped to by the given key
// Assumption: the key exists
//
// set : Eq V -> Dict<V>
// Set the given key-value mapping
Exercise 5. Create a new dictionary that uses this new data definition.
We’ve seen various implementations of dictionaries, but are they good for representing real dictionaries like the Merriam-Webster Dictionary that store words? You might think that since these dictionaries are specialized to work with words, you could design a faster data structure for them.
Well, it turns out you can. We will design a data structure called a "trie" (pronounced "tree" or "try") that is highly efficient for storing words. Here is the data definition for a trie:
// A Trie<V> is one of
// - new NoValue(Dict<Trie<V>>)
// - new Node(V, Dict<Trie<V>>)
// and implements Dict<V>
//
// where the keys in the Dict are all single-character strings
As you can see from the data definition, each trie node stores a dictionary of its child nodes keyed by single characters. Note: it will be helpful if your Dict implements the values method from earlier.
Imagine each connection from a node to its child as representing one character in a string. When you lookup a string in a trie, you look at the first character in the string and continue to lookup in the corresponding sub-trie. The path you take down the tree will spell out the string you are looking up.
For example, you could use a trie to store the frequencies of some given words in a document. Here is an example trie that stores numbers at each node to represent frequencies:
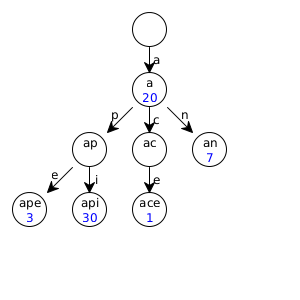
This tree stores the words "a", "ape", "api" (maybe it’s from a programming book that mentions apes), "ace", and "an". Note that this trie doesn’t store "ap" or "ac" because there are no values (no numbers) at these nodes, since neither are considered words in many documents.
The advantage of this representation is that the time it takes to lookup any string is proportional to the length of the string. This can be faster than using a binary search tree, which takes time proportional to the length times the logarithm of the height of the tree in the worst case.
Exercise 6. Write down the "Trie<V>" interface and the classes that implement it.
Implement has-key, lookup, and set for tries.
Since Java strings are not implemented as a data definition like a list, where you can take the first and rest, you will probably want to use the substring method.
There are a few other operations we might want on tries. For example, we might be interested in determining its size. This isn’t as simple as it sounds, because we only want to count strings that have a value in the trie, not just a node. In the example trie above, a size method should return 5.
// A Trie<V> also implements:
//
// size -> Integer
// find the size of a trie
Exercise 7. Implement size for tries.
Your trie implementation should be able to encode the trie example above. Here is some code that will build the example trie:
class TrieExamples {
Trie<V> exampleTrie;
public TrieExamples() {
// replace emptyTrie with your empty trie
Trie<V> exampleTrie =
emptyTrie.set("a", 20).set("ape", 3)
.set("api", 30).set("ace", 1)
.set("an", 7);
}
public boolean test1(Tester t) {
return t.checkExpect(exampleTrie.hasKey("api"), true);
}
public boolean test2(Tester t) {
return t.checkExpect(exampleTrie.size(), 5);
}
}
One of the operations that a trie makes very fast is searching for all key/value pairs that matches a certain prefix of a key (a prefix is just a substring of a string that includes the beginning). This kind of operation is useful if you want to search through a dictionary.
Here is a contract for a function that search the dictionary based on a prefix:
// A Trie<V> also implements:
//
// matchPrefix : String -> List<String>
// Finds all keys that match the given prefix
Exercise 8. Implement matchPrefix.
This prefix matching algorithm is actually an important one as it is one part of the procedure that routers on the Internet use to decide how to route traffic from one computer to another. Algorithms for IP routing use tries, albeit with much more complicated data definitions, to avoid storing the routing information for every single address. Instead, groups of IP addresses are assigned the same information when they share a prefix of their addresses.