Lab 10 Generative Recursion
Purpose: Practice designing generative recursion functions.
Textbook References: Chapter 25: Non-Standard Recursion, Chapter 26: Designing Algorithms
Harder, Better, Faster, Stronger
Your TAs will now demonstrate an example of using generative recursion to make a program faster. Please pay attention and be respectful.
There Is No Structure
; digit->string : Nat -> String ; Turn a single digit number into a single char string (define (digit->string n) (string (integer->char (+ 48 n)))) (check-expect (digit->string 5) "5") (check-expect (digit->string 0) "0")
Exercise 1 Design the function num->string that returns the string representation of a natural number (you may NOT use number->string). What is the base case for this function? What can we do to get from one digit to the next? Here are some tests for num->string:
(check-expect (num->string 0) "0") (check-expect (num->string 5) "5") (check-expect (num->string 1234) "1234") (check-expect (num->string 4321) "4321")
Fun With Fractals
For the next part of the lab you will design functions to draw (and iterate) some interesting fractal designs. A fractal is just a pattern that contains a smaller version of itself. Here are some examples:
One fractal design we can make is called the Dragon Fractal. This was used on the headings of chapters in the book Jurassic Park (if anyone is old enough to remember that...). We’ll start off by building a simple line drawing program. Then we’ll combine pieces into the fractal’s (generative) recursion.
; A Dir is a Symbol and is one of: ; - 'left ; - 'right ; - 'up ; - 'down
Exercise 2 Design the function, rotate-dir, that rotates a given Dir 90 degrees counter-clockwise (rotate to the left). What are the four cases of Dir and what should you return in each case?
Exercise 3 Design the function, rotate-all-dirs, that rotates all the Dirs in a [List-of Dir] counter-clockwise. Which pre-defined list abstraction can you use?
Exercise 4 Design the function move-posn that takes two Numbers, x and y, a Dir d, and a Number amnt and returns a Posn that is the result of moving the given x and y in the given direction, by the given amount.
Exercise 5 Design the function draw-all-dirs that consumes a [List-of Dir], two Numbers (an x and y coordinate), and an Image (a background to draw on), and draws lines in those directions (in order) starting at the given x and y onto the given image. You can use add-line to create the lines and choose some constant length for those lines.
Exercise 6 Put your functions together using big-bang to create an interactive line-drawing program. Use the arrow keys to create a path (a [List-of Dir]). You can hit r to rotate all the points to the left.
Exercise 7 Now we need to generate our fractal! Design a function jurassic which takes a [List-of Dir] and a Number (the iterations left to be done) and implements the algorithm as follows:
If the number is 0, return the given list as is.
Rotate all the Dirs from the old list counter-clockwise.
Reverse the rotated list.
Append the new reversed/rotated list on the end of the old list.
Recursively call jurassic on this new list with one less iteration.
(check-expect (jurassic '(down) 0) '(down)) (check-expect (jurassic '(down) 1) '(down right)) (check-expect (jurassic '(down) 2) '(down right up right)) (check-expect (jurassic '(down) 3) '(down right up right up left up right))
Exercise 8 Now we can develop a big-bang program to draw our fractals! Your Worldstate should be a natural number (the number of iterations to draw) and you should be able to hit the up and down arrow keys to increase or decrease the number of iterations of the fractal.
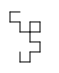
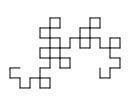
You may notice that after about 11 iterations, your fractal stops showing up properly. This is fine, it’s just that your fractal is too big to draw anymore. Below are some examples of what the fractal will look like after several iterations:
Number of iterations | Image of fractal |
0 |
|
2 |
|
4 |
|
6 |
|