 , which
we may write as
(cons
, which
we may write as
(cons  (cons
(cons  (cons ... (cons
(cons ... (cons 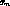 null) ... ))).
If we unwind the recursion, we have
null) ... ))).
If we unwind the recursion, we have
Consider a procedure that adds the numbers in a list:
(define sum (lon)
(if (null? lon)
0
(+ (car lon) (sum (cdr lon)))))
Suppose we apply sum to a list of numbers of length  , which
we may write as
(cons
, which
we may write as
(cons  (cons
(cons  (cons ... (cons
(cons ... (cons 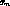 null) ... ))).
If we unwind the recursion, we have
null) ... ))).
If we unwind the recursion, we have
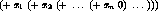
Observe that the conses in the input list have been replaced by the + operator. The replacement of a data constructor by a combining operator is the hallmark of a catamorphism.
Because addition is commutative, the last expression is equivalent to
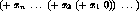
which corresponds to the code
(define sum2 (lon)
(sum2-help lon 0))
(define (sum2-help lon accum)
(if (null? lon)
accum
(sum2-help (cdr lon)
(+ (car lon) accum))))
Note that the recursive call is a tail-call.
These patterns occur often enough that we can write Scheme procedures to express them, foldr for the first pattern, and foldl for the second.
(define (foldr op starter lst)
(if (null? lst)
starter
(op (car lst)
(foldr op starter (cdr lst)))))
So we could have written
(define (sum lon)
(foldr + 0 lon))
Class exercise: write foldl.
In general, foldl and foldr will not produce equivalent results, because operations are not necessarily commutative.
In DrScheme, foldr and foldl are generalized to take one or more
list arguments. So if  list arguments are supplied, the op argument
takes
list arguments are supplied, the op argument
takes 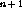 arguments -- the extra argument is for the accumulator.
arguments -- the extra argument is for the accumulator.
The fold and foldr functions use a function to extract
a value from a list. In general, one can create fold procedures
for any kind of tree-structured data. One can also imagine a function
that takes a value and generates a tree-like structure from it.
In fact, there is a lesser-known class of unfold functions,
which researchers have recently been studying. An example use of
unfold would be to take an input string and generate a list
of strings corresponding to sentences in the input.
(define (rem-by-pred lst)
(cond
[(null? lst) '()]
[(pred? (car lst))
(rem-by-pred (cdr lst))]
[else
(cons (car lst)
(rem-by-pred (cdr lst)))]))
This procedure discards elements that do satisfy a fixed
predicate. In DrScheme, the filter procedure takes a procedure
argument  and a list, and returns a list consisting of those elements
in the input for which
and a list, and returns a list consisting of those elements
in the input for which  does not return #f. So
filter works in a manner precisely opposite to rem-by-pred,
taking a procedure as an additional argument.
does not return #f. So
filter works in a manner precisely opposite to rem-by-pred,
taking a procedure as an additional argument.
Exercise: write filter.