Final Examination Solution
Com
1201 – Spring 2003 – Jeff Raab
Section 1 – Java programming
(30) Assume the following interface specifying the required methods for the Priority Queue ADT:
/**
* Required methods for the Priority Queue ADT.
* @author Jeff Raab
*/
public interface IPriorityQueue {
/**
* Inserts the given key and element into this.
* @param aKey key for the item
* @param anElement element for the item
*/
public void insertItem(Comparable key, Object element);
/** Returns a highest priority element in this. */
public Object highest();
/** Returns a highest priority key in this. */
public Comparable highestKey();
/**
* Removes the highest priority item from this,
* and returns its element.
*/
public Object removeHighest();
}
Assume also a class named Item whose data definition is a public Comparable named key and a public Object named element. You may assume that the Item class also has a constructor that takes in a Comparable and an Object as input, and stores those objects as the key and element, respectively, for the created Item object.
Write a class named UnsortedPriorityQueue that implements the IPriorityQueue interface by storing its keys and elements in an unsorted Java Vector. A summary of the HTML documentation for the Java Vector class is at the end of this test. You must use the Proxy design pattern for this class. Be sure to consider all of the error conditions you can identify and throw a RuntimeException in each case where an error occurs.
Your class must be correct and completely documented to the specification of the model code for a class as posted on the course website. Write your class and its documentation on the next two pages.
Section 1
answer
import java.util.Vector;
/**
* IPriorityQueue
implementation using a sorted vector
* to hold its keys
and elements.
* @author Jeff Raab
*/
public class UnsortedPriorityQueue implements IPriorityQueue {
/** Vector used to hold the keys and
elements. */
protected Vector
items = new Vector();
/** Constructs a new unsorted priority
queue. */
public UnsortedPriorityQueue() {}
/**
*
Inserts the given key and element into this.
* @param aKey key for the item
* @param anElement element for the
item
*
@example insertItem(1, A) into {} : {(1, A)}
*
@example insertItem(0, B) into {(1, A)} : {(1, A), (0, B)}
*/
public void insertItem(Comparable key, Object element) {
items.add(new Item(key, element));
}
/**
* Returns
a highest priority element in this.
*
@example highest() on {} throws an exception
*
@example highest() on {(1, A), (0, B)} returns B
*/
public Object
highest() {
if (items.isEmpty()) {
throw
new RuntimeException(“Queue is empty”);
}
Object o = items.elementAt(highestIndex());
Item i =
(Item)o;
return i.element;
}
/**
* Returns a highest priority key in this.
* @example highestKey() on {} throws an
exception
* @example highestKey() on {(1, A), (0,
B)} returns 0
*/
public Comparable highestKey() {
if (items.isEmpty()) {
throw new RuntimeException(“Queue
is empty”);
}
Object
o = items.elementAt(highestIndex());
Item
i = (Item)o;
return i.key;
}
/**
*
Removes the highest priority item from this,
* and returns its element.
*
@example removeHighest() on {} throws an exception
*
@example removeHighest() on {(1, A), (0, B)} returns B
*/
public Object removeHighest() {
if (items.isEmpty()) {
throw
new RuntimeException(“Queue is empty”);
}
Object o = items.remove(highestIndex());
Item i =
(Item)o;
return i.element;
}
/** Returns the index of the highest key in
this. */
private int highestIndex() {
int min = 0;
Item minItem
= (Item)items.elementAt(0);
for (int i = 1; i < items.size();
i++) {
Item anItem
= (Item)items.elementAt(i);
if (anItem.key.compareTo(minItem.key)
< 0) {
min
= i;
minItem = anItem;
}
}
return min;
}
}
Section
2 – Short answer questions
(10) 1. Using the Proxy design pattern, is it possible to implement the Priority Queue ADT using a binary search tree implementation of the Dictionary ADT? The methods in these two ADTs are given at the end of this test. You may assume that you could add any further data or methods to the binary search tree class as you like.
If it is possible, describe in reasonable detail how the insertItem, highest, and removeHighest methods would be implemented. You don’t have to write the code, just explain how it would work. Using Big-Oh notation, list the running time for each of these methods.
If it is not possible, describe in reasonable detail why it is so. Be specific. It is not good enough for you to write that you simply “think” it is not possible.
Draw diagrams if necessary, to further explain your ideas.
Yes, it is possible to implement the
Priority Queue ADT using a binary search tree implementation of the Map
ADT. A Priority Queue must store, or
otherwise be able to find, the highest priority key in the structure. Because the binary search condition requires
that the key for a node must be greater than the key in its left child, we know
that smaller keys are always on the left of the tree. Specifically, the minimum key is in the node
you reach by starting at the root and following to the left child of each node
until there is no left child.
The insertItem
method would be proxied directly to the insertItem method in the search tree. This would take O(n) time, because if unbalanced, the height of a binary search tree
is O(n).
The highest method would search for the
highest priority key using the method described above, and return an item
associated with that key. This would
take O(n) time, because if the tree is
unbalanced and all keys were inserted into the tree in decreasing order, the
height is O(n).
The removeHighest
method would retrieve the highest key in the priority queue using the highestKey method, and then remove it and its associated
element from the search tree by proxying to the removeElement method.
This would take O(n) time, because it would take O(n)
time to find the highest key and O(n) time to remove an element from the
tree.
Since a map must have unique keys, but a
priority queue does not have this requirement, the search tree must be able to
associate multiple elements to the same key.
In a binary search tree this is simply implemented by associating a
linear structure, such as a nonrecursive list, with
each key.
(10) 2. Using the Proxy design pattern, is it possible to implement the Stack ADT using an implementation of the Priority Queue ADT? The methods in these two ADTs are given at the end of this test. You may not assume any particular implementation of the Priority Queue ADT, such as a heap or sorted list. All you know is that you have a Priority Queue to work with. You may assume that you could add any further data or methods to the stack class as you like.
If it is possible, describe in reasonable detail how the push, pop, and top methods would be implemented. You don’t have to write the code, just explain how it would work. Using Big-Oh notation, list the running time for each of these methods.
If it is not possible, describe in reasonable detail why it is so. Be specific. It is not good enough for you to write that you simply “think” it is not possible.
Draw diagrams if necessary, to further explain your ideas.
Yes, it is possible to implement the Stack ADT using an implementation
of the Priority Queue ADT. Since a
priority queue works in a highest priority in, first out manner and a stack
works in a last in, first out manner, we just have to make sure the last inserted
item has the highest priority.
The push method would proxy to the insertItem
method in the priority queue, passing a key of –size(),
and the given element as parameters. The
running time for this method depends on the priority queue implementation that
is used. It can range anywhere from O(1) for an
unsorted list, O(log n) for a heap, or O(n) for a sorted list.
The pop and top methods would proxy directly to the removeHighest
and highest methods in the priority queue, respectively. The running times for these methods depend on
the priority queue implementation that is used.
They can range anywhere from O(1)
and O(1) for an sorted list, O(log n) and O(1) for a heap,
or O(n) and O(n) for an unsorted list.
Section 3 – Diagrammatic questions
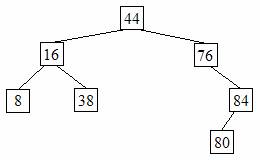
(10) 1. Show the binary search tree that results from inserting items with the following keys into an empty binary search tree implementation of the Dictionary ADT. The keys must be inserted in this given order from left to right. You don’t have to show the elements in the binary search tree, just the keys.
|
Keys |
44 |
16 |
76 |
84 |
38 |
80 |
8 |
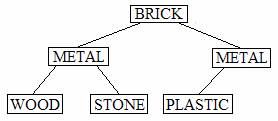
(10) 2. Show the heap that results from inserting items with the following keys into a heap implementation of the Priority Queue ADT. The keys must be inserted in this given order from left to right. Assume that priority is defined by standard English dictionary (lexicographical) order where words that begin with the letter A are higher priority than those starting with the letter B, and so on. You do not have to show the elements in the heap, just the keys.
|
Keys |
WOOD |
PLASTIC |
METAL |
STONE |
BRICK |
METAL |
(5) 3. Show the contents of the array that
results from performing the following operations on a sorted array
implementation of the Priority Queue ADT.
The operations must be performed in this given order from left to
right. You do not have to show the
elements in the array, just the keys.
Write the word “null” in any array locations in which no item is
stored. Fill in the following array
diagram with your answer, for these given operations:
|
Operations |
insertItem(3) |
insertItem(0) |
removeHighest() |
removeHighest() |
insertItem(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
null |
null |
null |
null |
null |
null |
null |
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
length = 8 |
|||||||||
(5) 4. Show the contents of the array that results from performing the following operations on an open addressing hashtable implementation of the Dictionary ADT that uses the linear probing style of collision handling. The operations must be performed in this given order from left to right. Use the following hash function:
h(k) = | 3k + 1 | mod 11
You do not have to show the elements in the array, just the keys. Place an X in the array to represent a location where an item was stored, but is no longer there.
Fill in the following array diagram with your answer, for these given operations:
|
Operations |
insertItem(1) |
insertItem(4) |
removeElement(1) |
insertItem(-4) |
removeElement(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-4 |
|
4 |
|
X |
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
length = 11 |
||||||||||||
Section 4 – Data structures
For each situation below, list the ADT you would choose for the specified task, and the implementation of that ADT that would provide the most efficient running time for each of the operations listed in the problem. Please use asymptotic analysis for the running time, and use Big‑Oh and Big‑Theta as appropriate.
(10) 1. You are employed by a software company designing an application to read and write email messages. Your job is to implement the data structure used to store a collection of Contact objects, where a Contact object contains a name, email address, etc. The structure must be able to add a new Contact at the end of the collection, remove a Contact from any location in the collection, and count the number of Contacts in the collection.
Your choice of ADT would be: List ADT
Your choice of implementation would be: Nonrecursive list
|
Operation |
Method in ADT used to implement |
Running time |
|
Add contact to the collection |
insertLast |
O(1) |
|
Remove a contact |
remove |
O(1)
or O(n) |
|
Count the number of contacts |
size |
O(1) |
(10) 2. You are employed by a software company designing an application for use by college admissions committees. Your job is to implement the data structure used to maintain the “waiting list”. The data structure must be able to associate a standardized test score with a student ID number, get the highest test score among the students on the waiting list, and remove the most qualified student from the waiting list (when there becomes room to admit one more student.)
Your choice of ADT would be: Priority Queue ADT
Your choice of implementation would be: Heap
|
Operation |
Method in ADT used to implement |
Running time |
|
Associate score with student |
insertItem |
O(log
n) |
|
Get highest score |
highestKey |
O(1) |
|
Remove most qualified student |
removeHighest |
O(log
n) |