Midterm Examination Solution
Com 1201 Winter 2003 Jeff Raab
Section
1 Java Programming
(10)  The flag of the
The flag of the
Write a method below named stripes
that takes one parameter named count of type int
and has a return type of boolean. This method must return true
if it is possible to create a flag whose layout of stripes is similar to that
of the
For the purposes of this problem, zero is an even number. It is not possible to create a flag with a negative number of stripes. Your method must be correct and completely documented to the specification of the model code for a function as posted on the course website. Write your function and its documentation in the space below:
/**
*
Returns whether or not a flag could be created
* with
the given number of stripes.
*
@example stripes(-1) returns false
*
@example stripes(2) returns false
*
@example stripes(3) returns true
*
@example stripes(4) returns false
*
@param count number of stripes
*/
public boolean stripes(int count) {
if
(count < 3)
return
false;
return
(count % 2 == 1);
}
All that you must do in this problem is
determine if it is possible to create a flag with the given number of
stripes. You have to determine if some
number of reds and whites exists whose sum equals count. You just need an odd number of stripes
greater than 1. Note that no exceptions
are thrown in this method, as you are just to return false if the given number
doesnt fit the specification for the stripes in the flag.
The running time for this method,
as you have written it, is O(1) .
(15) Write a method below named stars
that takes one parameter named count of type int
and has a return type of boolean. This method must return true
if it is possible to create a flag whose layout of stars is similar to that of
the
1. The stars are in rows of alternating lengths.
2. The lengths of the rows differ by exactly one.
3. There are at least 3 rows of stars.
4. There is one more row of the longer length than of the shorter length.
5. The number of stars is equal to the given count.
This method must return false if it is not possible to create a flag that meets these criteria.
It is not possible to create a flag with a negative number of stars. Your method must be correct and completely documented to the specification of the model code for a function as posted on the course website. Write your function and its documentation in the space below:
/**
*
Returns whether or not a flag could be created
* with
the given number of stars.
*
@example stars(-1) returns false
*
@example stars(3) returns false
*
@example stars(5) returns true
*
@example stars(6) returns false
*
@param count number of stars
*/
public boolean stars(int count) {
if
(count < 5)
return
false;
int
perCol = 3;
for
(int rows = 5; rows < count; rows += 3) {
for
(int cols = 0; cols < count; cols++) {
if
(rows + (cols * perCol) == count) {
return
true;
}
}
perCol
+= 2;
}
return
false;
}
The algorithm for this problem is difficult, but the structure of the
code is the same as for the previous method.
It is probably possible to try a series of modulus calculations in O(n)
time, but the above is easier to understand, I think.
The above code takes the smallest possible configuration of 5 stars and
adds 1 column to it, over and over, to try and equal the appropriate number of
stars. If that doesnt work, it tries 5
rows with 8 stars, and adds 1 column per time to try and equal the right
number. If that doesnt work it tries 7
rows, then 9 rows, &c. until it can be proven that the given number of
stars doesnt have a possible configuration.
The running time for this method, as you have written it, is O(n2)
.
For this section, the following things were required:
Documentation
with purpose, examples, and param descriptions
Method
header
Method
body with correct algorithm
Section
2 Implementing a Java interface
(30) The Deck interface describes a data structure used to store and retrieve Objects in the same manner as a deck of cards. Assume the following code:
/**
Interface describing the operations for a deck. */
public
interface Deck {
/**
*
Adds the given element to the bottom of this deck.
*
@param element object to be added
*/
public void add(Object element);
/**
*
Inserts the given element at a random position
* in
this deck.
*
@param element object to be inserted
*/
public void insert(Object element);
/**
* Removes the object on the top
of this deck,
* and returns that object.
*/
public Object removeTop() throws RuntimeException;
/** Returns the number of objects in this
deck. */
public int size();
/** Returns whether or not this deck is
empty. */
public boolean isEmpty();
}
On the following page, write a complete Java class named VectorDeck that implements this ADT using a Java Vector object to do the work of the methods required by the interface. The last pages of this exam summarize the documentation for the Vector class, for your reference.
The following code stores a random integer in the range [0, n) in the variable k:
int k
= (int)(Math.random() * n);
Your method must be correct and completely documented to the specification of the model code for a class as posted on the course website. Write your class and its documentation on the next page.
Section
2 answer
import java.util.*;
/**
*
Implementation of the Deck interface using a Vector.
*
@author Jeff Raab
*/
public class VectorDeck implements Deck {
/**
Vector used to store elements. */
protected
Vector elements = new Vector();
/**
Constructs a new VectorDeck. */
public
VectorDeck() {}
/**
* Adds the given element to the bottom of this
deck.
* @param element object to be added
*/
public void add(Object
element) {
elements.add(element);
}
/**
* Inserts the given element at a random
position
* in this deck.
* @param element object to be inserted
*/
public void insert(Object
element) {
elements.add((int)(Math.random() * size(), element));
}
/**
* Removes the object on the top of this deck,
* and returns that object.
*/
public
Object removeTop() throws RuntimeException {
return
elements.remove(0);
}
/**
Returns the number of objects in this deck. */
public
int size() {
return
elements.size();
}
/**
Returns whether or not this deck is empty. */
public
boolean isEmpty() {
return
elements.isEmpty();
}
}
There is no need to grow and shrink the Vector, as that is what the
class does for you automatically during add and remove operations. It is inappropriate to extend the Vector
class because that exposes methods that could be used to circumvent the idea of
the Deck as described in the interface.
(For example, it allows removal of elements other than from the top of
the deck.)
Note that the remove method used in removeTop will throw a runtime
exception if the deck is empty. If you
explicitly threw an exception in the proper case, thats fine too.
For this section, the following things were required:
Import
of the Vector class
Class
documentation comment with purpose of class
Class
header
Protected
Vector data member for class
Documentation
comment for data member with its purpose
Constructor
All
methods in the Deck interface
Method
bodies with correct algorithms
Documentation
comments for each method
If you included your name in the class documentation comment, I went
easy on the import statement. If you
stated in a documentation comment for each method that you copied that
documentation comment from the interface definition, that was fine too.
Section
3 Analysis
Analyze each function. Write the number of * characters it actually prints, in terms of the values of any inputs to the function. Provide an asymptotic analysis of the number of * characters printed, in terms of the values of any inputs to the function. In case you are unsure, the following code prints a single * character:
System.out.println(*);
The following code prints three * characters:
System.out.println(***);
Be sure to completely read the code of each function before performing your analysis of it.
(5) public void printStars1(int
n) {
System.out.println(***);
for
(int i = 0; i < n; i++) {
for (int j = 0; j < 50; j++) {
System.out.println(*);
}
}
System.out.println(**);
}
The number of * characters actually
printed is 50n + 5 .
Asymptotically, the number of * characters printed is O(n) .
(5) public void printStars2(int
n) {
System.out.println(**********);
}
The number of * characters
actually printed is 10 .
Asymptotically, the number of * characters printed is O(1) .
Section
3 Analysis
Analyze each function. Write the number of * characters it actually prints, in terms of the values of any inputs to the function. Provide an asymptotic analysis of the number of * characters printed, in terms of the values of any inputs to the function. In case you are unsure, the following code prints a single * character:
System.out.println(*);
The following code prints three * characters:
System.out.println(***);
Be sure to completely read the code of each function before performing your analysis of it.
(5) public void printStars3(int
n) {
System.out.println(***);
int
pow = 1 * 2 * 3 * 4;
for
(int i = 0; i < pow; i++)
System.out.println(**);
System.out.println(***);
}
The number of * characters
actually printed is 2(4!) + 6, which
equals 54 .
Asymptotically, the number of * characters printed is O(1) .
(10) public void printStars4(int
n) {
System.out.println(**);
for
(int i = 0; i < n; i++) {
System.out.println(**);
System.out.println(*);
}
System.out.println(*);
}
The number of * characters
actually printed is 3n + 3 .
Asymptotically, the number of * characters printed is O(n) .
Section 4 Linked Lists
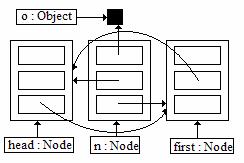
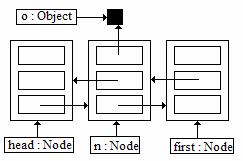
(20) Assume a linked list class constructed from nodes that each contain three references: one for the element Object the node contains, one that refers to the next node in the list, and one that refers to the previous node in the list. You must draw diagrams that show the state of the nodes in the list during the process of inserting a new node immediately after the head sentinel node.
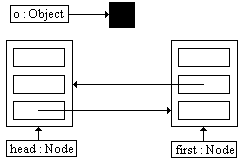
The diagram below shows the state of the list before inserting. Draw one diagram per step, in the boxes below, that shows the state of the list after that step is performed. Use the given diagram as a guide for the correct way to draw a linked list. References to null can be left blank. Feel free to ask if your diagrams are understandable, to ensure that you get proper credit.
|
Before insert of object o at the front of the list
|
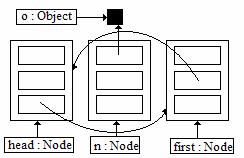
Create a new node n that refers to o
|
|
Set the previous for n to the head
|
Set the next for n to the first node after the head
|
|
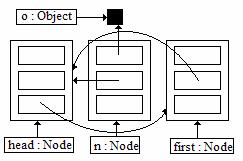
Set the next for the head to n
|
Set the previous for the first node after head to n
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|