Final Examination Solution
Com 1201 – Winter 2003 – Jeff Raab
Section 1 – Java programming
(5) 1. Write a public method below named search that takes an array of int values named a, an int value named v, and has a return type of boolean. Your method must return true if the given array contains the given value, or false in every other case. Your method must be correct and completely documented to the specification of the model code for a function as posted on the course website. Write your function and its documentation in the space below.
Analyze your method by using Big-Oh notation to generalize the number of steps in the worst case.
/**
* Returns true if the given value is in the
given array,
* or false otherwise.
* @example search(1, {1,2,3,4,5}) returns true
* @example search(6, {1,2,3,4,5}) returns false
* @example search(1, {}) returns false
* @example search(1, null) returns false
* @param v value to search for
* @param a array of values to search
*/
public
boolean search(int v, int[] a) {
if (a == null) {
return false;
}
for (int i = 0; i < a.length; i++) {
if (v == a[i]) {
return true;
}
}
return false;
}
Using Big-Oh notation, the number of steps is O(n) .
Section 1 – Java programming
(10) 2. Write a public method below named searchSorted that takes a sorted array of int values named aSorted, an int value named v, and has a return type of boolean. Your method must return true if the given array contains the given value, or false in every other case. Your method must be correct and completely documented to the specification of the model code for a function as posted on the course website. Write your function and its documentation in the space below.
Analyze your method by using Big-Oh notation to generalize the number of steps in the worst case.
/**
* Returns true if the given value is in the
given array,
* or false otherwise.
* @example searchSorted(1, {1,2,3,4,5})
returns true
* @example searchSorted(6, {1,2,3,4,5})
returns false
* @example searchSorted(1, {}) returns false
* @example searchSorted(1, null) returns false
* @param v value to search for
* @param a sorted array of values to search
*/
public
boolean searchSorted(int v, int[] a) {
if (a == null) {
return false;
}
for (int i = 0; i < a.length; i++) {
if (v == a[i]) {
return true;
}
if
(v < a[i]) {
return false;
}
}
return false;
}
Using Big-Oh notation, the number of steps is O(n) .
Section 1 – Java programming
(10) 3. Write a public method below named searchSortedList that takes the head Node of a sorted list of int values named n, an int value named v, and has a return type of boolean. Your method must return true if the given list contains the given value, or false in every other case. Your method must be correct and completely documented to the specification of the model code for a function as posted on the course website. Write your function and its documentation in the space below.
You may assume that the Node class has three data members: element of type int, previous of type Node, and next of type Node. The given node n will contain the first int in the list and is not a sentinel node. Assume there is no sentinel node at the end of the list, and that the last node in the list has its next reference set to null.
Analyze your method by using Big-Oh notation to generalize the number of steps in the worst case.
/**
* Returns true if the given value is in the
given list,
* or false otherwise.
* @example searchSortedList(1, {1,2,3,4,5})
returns true
* @example searchSortedList(6, {1,2,3,4,5})
returns false
* @example searchSortedList(1, {}) returns
false
* @example searchSortedList(1, null) returns
false
* @param v value to search for
* @param n head node of sorted list to search
*/
public
boolean searchSortedList(int v, int[] a) {
while (n != null) {
if (v == n.element) {
return true;
}
if
(v < n.element) {
return false;
}
}
return false;
}
Using Big-Oh notation, the number of steps is O(n) .
Section 2 – Short answer questions
(10) 1. Is it possible to use an implementation of the Dictionary ADT to implement the Queue ADT? The design for such a class would be as follows:
/**
Dictionary implementation of the Queue ADT. */
public class DictionaryQueue implements QueueADT {
/** Dictionary used to hold the elements. */
protected DictionaryADT d;
. . .
}
The . . . shows where the rest of the class definition would go.
If it is possible to implement the Queue ADT using methods of the Dictionary ADT, describe in reasonable detail how the enqueue, dequeue, and front methods would be implemented. You don’t have to write the code, just explain how it would work.
If it is not possible, explain why it is so.
It is possible to implement the Queue ADT
using the Dictionary ADT. Add two int
counter variables to the data definition of DictionaryQueue above. These counters will represent the keys for the
front and back elements on the queue, respectively. The front method would just retrieve the
element associated with the front key from the dictionary. The enqueue method would increment the back counter,
and insert an item in the dictionary using that key and the element given to
enqueue. The dequeue method would remove
the element associated with the front key from the dictionary and increment the
front counter.
(10) 2. Describe in reasonable detail a way to implement the Dictionary ADT such that the insertItem, findElement, and removeElement methods would all run in O(1) time, assuming that all of the keys associated with elements in the structure are integers in the range [10, 25). You do not have to ensure that the remaining Dictionary ADT methods would have any particular running times, and you do not have to describe how those remaining methods would be implemented.
Describe how much memory would be used by such a structure, using Big-Oh notation. For example, if you described an unsorted sequence implementation of the Dictionary ADT, you would state that your structure would use 1 sequence of size n, which is O(n).
Given the range of keys, a hash table array
of length 15 could be used to implement the Dictionary ADT. The hash function for the table would be h(k)
= k – 10. Separate chaining would be the collision
handling strategy for the hash table, with unsorted lists used to hold the elements
associated with the key represented by that index. insertItem would hash the key and insert into the
unsorted list at the resulting index: O(1).
findElement would hash the key and return the first
element of the list, unless it was empty: O(1).
removeElement would hash the key and remove the first
element of the list, unless it was empty: O(1).
The memory used by this structure is an
array of 15 lists, which is 15 + O(n) units of memory, or O(n).
Section 3 – Diagrammatic questions
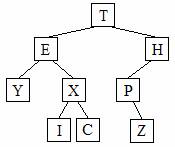
(5) 1. List the order in which the contents of the following tree would be visited, for each of the given traversals:
|
Traversal |
Visit order |
||||||||
|
Preorder |
T |
E |
Y |
X |
I |
C |
H |
P |
Z |
|
Postorder |
Y |
I |
C |
X |
E |
Z |
P |
H |
T |
|
Inorder |
Y |
E |
I |
X |
C |
T |
P |
Z |
H |
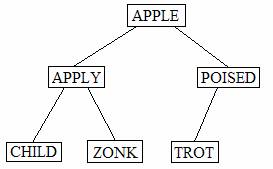
(10) 2. Show the heap that results from inserting items with the following keys into a heap implementation of the Priority Queue ADT. The keys must be inserted in order from left to right. Assume that priority is defined by standard English dictionary (lexicographical) order where words that begin with the letter A are higher priority than those starting with the letter B, and so on. You do not have to show the elements, just the keys.
|
Keys |
CHILD |
APPLE |
TROT |
APPLY |
ZONK |
POISED |
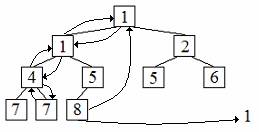
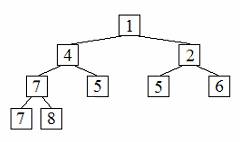
(5) 3. Draw the heap that results from removing a minimum key from the heap shown below. On the given heap diagram, use arrows to show which nodes had their keys swapped during the process of reestablishing the heap condition. As in the given diagram, you do not have to show the elements associated with the keys.
(5) 4. List the contents of the array for an open addressing hashtable using the linear probing style of collision handling, after performing the given Dictionary ADT operations in order. Use the following hash function:
h(k) = | 2k + 5 | mod 11
You should ignore the elements associated with the given keys as they could be any objects and do not affect the resulting order. Place an X in the array to indicate an empty location that used to contain a key.
Fill in the following array diagram with your final answer, for these given operations:
|
Operations |
|
insertItem(3) |
|
insertItem(14) |
|
insertItem(3) |
|
removeElement(0) |
|
removeElement(3) |
|
insertItem(6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
14 |
3 |
|
|
|
6 |
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
length = 11 |
||||||||||||
Section 4 – Data structures
For each situation below, list the ADT you would choose for the specified task, and the implementation of that ADT that would provide the most efficient running time for each of the operations listed in the problem. Please use asymptotic analysis for the running time, and use Big‑Oh and Big‑Theta as appropriate.
(10) 1. You are employed by a software company designing an application for use by produce wholesalers. Your job is to implement the data structure used to store the inventory of the warehouse containing the produce. The data structure must be able to add a product with an associated code indicating its likelihood to spoil, remove a product that is most likely to spoil (to ship it from the warehouse), and return the overall number of products in the inventory. No other functionality is needed.
Your choice of ADT would be: Priority Queue ADT
Your choice of implementation would be: Heap
|
Operation |
Method in ADT used to implement |
Running time |
|
Add a product and its code |
insertItem |
O(log
n) |
|
Remove a product likely to spoil |
removeMin |
O(log
n) |
|
Return the number of products |
size |
O(1) |
(10) 2. You are employed by a software company designing an application for use by taxicab dispatchers. Your job is to implement the data structure used to associate customers with taxicabs. The data structure must be able to associate a customer’s address with a taxicab’s number, find the address associated with a taxicab’s number, and remove the association between an address and a taxicab number (when the customer has been delivered to its destination. No other functionality is needed.
Your choice of ADT would be: Dictionary ADT
Your choice of implementation would be: Hash table
|
Operation |
Method in ADT used to implement |
Running time |
|
Associate address with taxicab |
insertItem |
O(n) |
|
Find address associated with taxi |
findElement |
O(n) |
|
Remove address and taxicab association |
removeElement |
O(n) |